Analyse – Rijen en reeksen – Machtreeksen

Definitie: Een reeks van de vorm

\[\sum_{n=0}^{\infty}c_nx^n=c_0+c_1x+c_2x^2+\cdots\]

heet een machtreeks in \(x\). De constanten \(\{c_n\}_{n=0}^{\infty}\) heten de coëfficiënten van de machtreeks.

Meer algemeen, een reeks van de vorm

\[\sum_{n=0}^{\infty}c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+\cdots\]

heet een machtreeks in \(x-a\) of een machtreeks gecentreerd in \(x=a\) of een machtreeks rond \(a\).

Voorbeelden:

1) De machtreeks \(\displaystyle\sum_{n=0}^{\infty}x^n\) is een meetkundige reeks met reden \(x\). Dus, deze machtreeks is absoluut convergent als \(|x| < 1\) en is divergent als \(|x|\geq1\). Verder geldt, voor \(|x| < 1\) is de om van de reeks gelijk aan \(\displaystyle\frac{1}{1-x}\).

2) De reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{(x-2)^{n-1}}{n}\) is een machtreeks rond \(2\). Merk op dat de reeks convergeert voor \(x=2\) (met som \(1\)). Voor \(x\neq2\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle\frac{(x-2)^{n-1}}{n}\), dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(x-2)^n}{n+1}\cdot\frac{n}{(x-2)^{n-1}}\right| =\lim\limits_{n\to\infty}\frac{n}{n+1}\cdot|x-2|=|x-2|.\]

Dus, de reeks is absoluut convergent als \(|x-2| < 1\) en is divergent als \(|x-2| > 1\). Het quotiëntkenmerk geeft geen uitsluitsel als (|x-2|=1\).

Voor \(x=3\) is de reeks gelijk aan de harmonische reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\) en die is divergent.

Voor \(x=1\) is de reeks gelijk aan de alternerende harmonische reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\) en die is (voorwaardelijk) convergent.

We concluderen dat de reeks convergeert als \(x\in[1,3)\) en anders divergeert. Het interval \([1,3)\) heet het convergentie-interval (ook wel: convergentiegebied) van de reeks.

Stelling: Voor een gegeven machtreeks

\[\sum_{n=0}^{\infty}c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+\cdots\]

zijn er slechts drie mogelijkheden:

1. De reeks convergeert alleen voor \(x=a\) (dan is de convergentiestraal \(R=0\)),


2. De reeks convergeert voor alle \(x\) (dan is de convergentiestraal \(R=\infty\)),


3. Er bestaat een positief getal \(R\) (de convergentiestraal) zodat de reeks absoluut convergeert voor \(|x-a| < R\) en divergeert voor \(|x-a| > R\).

Voorbeelden:

1) De reeks \(\displaystyle\sum_{n=0}^{\infty}n!(x-1)^n\) is een machtreeks rond \(1\). Dus, de reeks convergeert voor \(x=1\) (met som \(1\)). Voor \(x\neq1\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=n!(x-1)^n\), dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(n+1)!(x-1)^{n+1}}{n!(x-1)^n}\right| =\lim\limits_{n\to\infty}(n+1)|x-1|=\infty,\]

omdat \(|x-1| > 0\). Hieruit volgt dat de reeks divergeert voor alle \(x\neq1\). Dus, de reeks convergeert alleen voor \(x=1\) en de convergentiestraal is \(R=0\).

2) De reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{(x+2)^n}{n!}\) is een machtreeks rond \(-2\). Dus, de reeks convergeert voor \(x=-2\) (met som \(1\)). Voor \(x\neq-2\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle\frac{(x+2)^n}{n!}\), dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(x+2)^{n+1}}{(n+1)!}\cdot\frac{n!}{(x+2)^n}\right| =\lim\limits_{n\to\infty}\frac{|x+2|}{n+1}=0.\]

Hieruit volgt dat de reeks ook convergeert voor alle \(x\neq-2\). Dus, de reeks convergeert voor alle \(x\in\mathbb{R}\) en de convergentiestraal is \(R=\infty\).

3) De reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{x^{n+1}}{n^2}\) is een machtreeks rond \(0\). Dus, de reeks convergeert voor \(x=0\) (met som \(0\)). Voor \(x\neq0\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle\frac{x^{n+1}}{n^2}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{x^{n+2}}{(n+1)^2}\cdot\frac{n^2}{x^{n+1}}\right| =\lim\limits_{n\to\infty}\left(\frac{n}{n+1}\right)^2|x|=|x|.\]

Hieruit volgt dat de reeks absoluut convergeert voor \(|x| < 1\) en divergeert voor \(|x| > 1\). De convergentiestraal is dus \(R=1\). Voor \(x=1\) geldt \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}\) en dat is een \(p\)-reeks met \(p=2>1\) en is dus (absoluut) convergent. Voor \(x=-1\) geldt \(\displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}\) en die is ook absoluut convergent. Dus, het convergentie-interval is \([-1,1]\).

4) De reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{(3-x)^n}{n+1}\) is een machtreeks rond \(3\). Dus, de reeks convergeert voor \(x=3\) (met som \(1\)). Voor \(x\neq3\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle\frac{(3-x)^n}{n+1}\), dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(3-x)^{n+1}}{n+2}\cdot\frac{n+1}{(3-x)^n}\right| =\lim\limits_{n\to\infty}\frac{n+1}{n+2}\cdot|3-x|=|3-x|.\]

Dus, de reeks is absoluut convergent als \(|3-x| < 1\) en is divergent als \(|3-x| > 1\). De convergentiestraal is dus \(R=1\). Voor \(x=2\) is de reeks gelijk aan de harmonische reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n+1}\) en die is divergent en voor \(x=4\) is de reeks gelijk aan de alternerende harmonische reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^n}{n+1}\) en die is (voorwaardelijk) convergent. Dus, het convergentie-interval is \((2,4]\).

5) De reeks \(\displaystyle\sum_{n=1}^{\infty}n\left(\frac{x-5}{2}\right)^n\) is een machtreeks rond \(5\). Dus, de reeks convergeert voor \(x=5\) (met som \(0\)). Voor \(x\neq5\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle n\left(\frac{x-5}{2}\right)^n\), dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|(n+1)\left(\frac{x-5}{2}\right)^{n+1}\cdot\frac{1}{n}\left(\frac{2}{x-5}\right)^n\right| =\lim\limits_{n\to\infty}\frac{n+1}{n}\cdot\left|\frac{x-5}{2}\right|=\left|\frac{x-5}{2}\right|.\]

Dus, de reeks is absoluut convergent als \(\displaystyle\left|\frac{x-5}{2}\right| < 1\) of \(|x-5| < 2\) en is divergent als \(\displaystyle\left|\frac{x-5}{2}\right| > 1\) of \(|x-5| > 2\). Dus, de convergentiestraal is \(R=2\). Voor \(x=7\) is de reeks \(\displaystyle\sum_{n=1}^{\infty}n\) en die is divergent en voor \(x=3\) is de reeks \(\displaystyle\sum_{n=1}^{\infty}n(-1)^n\) en die is ook divergent. Dus, het convergentie-interval is \((3,7)\).

Besselfuncties

Stewart §11.8, Voorbeeld 3
Besselfuncties worden gedefinieerd in termen van machtreeksen. De Duitse astronoom Friedrich Bessel (1784-1846) introduceerde deze functies bij het oplossen van de vergelijking van Kepler voor de beschrijving van planeetbewegingen. Later werden deze Besselfuncties toegepast op diverse fysische problemen, zoals de temperatuurverdeling in een cirkelvormige plaat en de vorm van een trillend trommelvel.\({}^{(*)}\)

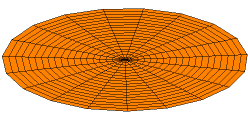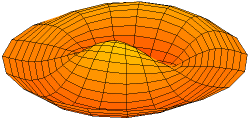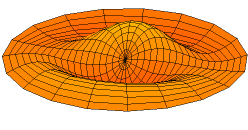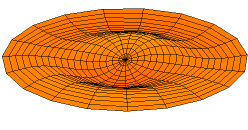
De Besselfunctie van de eerste soort van orde \(0\) wordt gedefinieerd door: \(J_0(x)=\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{2^{2n}(n!)^2}\).

Merk op dat dit een machtreeks in \(x\) is die convergent is voor \(x=0\). Voor \(x\neq0\) kunnen we het quotiëntkenmerk toepassen: laat \(a_n=\displaystyle\frac{(-1)^nx^{2n}}{2^{2n}(n!)^2}\), Dan geldt:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(-1)^{n+1}x^{2n+2}}{2^{2n+2}((n+1)!)^2}\cdot\frac{2^{2n}(n!)^2}{(-1)^nx^{2n}}\right| =\lim\limits_{n\to\infty}\frac{x^2}{4(n+1)^2}=0.\]

Dus, de reeks convergeert ook voor alle \(x\neq0\). We concluderen dat de machtreeks convergeert voor alle \(x\in\mathbb{R}\) (de convergentiestraal is \(R=\infty\). Hieruit volgt dat het domein van de Besselfunctie \(J_0(x)\), het convergentiegebied van de reeks, gelijk is aan \((-\infty,\infty)=\mathbb{R}\).

(*) Bron: https://en.wikipedia.org/wiki/Vibrations_of_a_circular_membrane.

---

Laatst gewijzigd op 15 maart 2021