Analyse – Rijen en reeksen – Het integraalkenmerk

We hebben al gezien: de harmonische reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\) is divergent.

Bewijs gebaseerd op het integraalkenmerk:


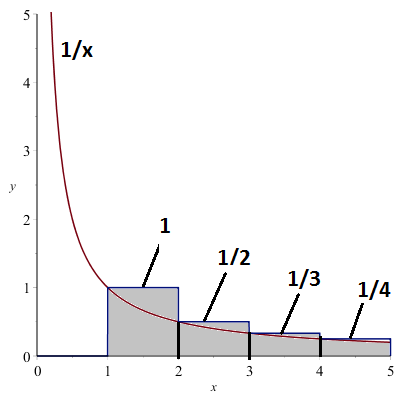
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots > \int_1^{\infty}\frac{1}{x}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\infty\).

Evenzo geldt: de reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}\) is convergent.

Bewijs gebaseerd op het integraalkenmerk:


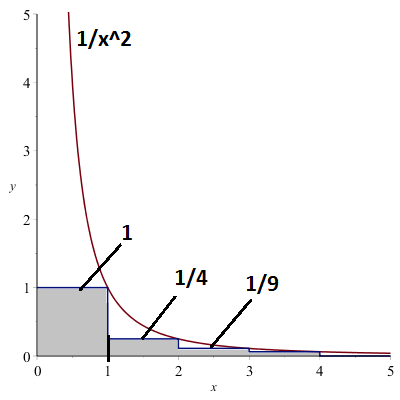
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\cdots < \int_1^{\infty}\frac{1}{x^2}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x^2}\,dx=1\).

Het integraalkenmerk

Stelling: Neem aan dat \(f\) een continue, positieve en dalende functie is op \([1,\infty)\) en laat \(a_n=f(n)\). Dan geldt:

\[\sum_{n=1}^{\infty}a_n\;\;\text{is convergent}\quad\Longleftrightarrow\quad\int_1^{\infty}f(x)\,dx\;\;\text{is convergent.}\]

Met andere woorden:

1. Als \(\displaystyle\int_1^{\infty}f(x)\,dx\) convergent is, dan is ook \(\displaystyle\sum_{n=1}^{\infty}a_n\) convergent.


2. Als \(\displaystyle\int_1^{\infty}f(x)\,dx\) divergent is, dan is ook \(\displaystyle\sum_{n=1}^{\infty}a_n\) divergent.

Merk op dat het niet noodzakelijk is om te beginnen bij \(1\) (zowel voor de reeks als voor de integraal) en dat \(f\) op den duur dalend moet zijn.

Stewart §11.3, Voorbeeld 1
Beschouw de reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n^2+1}\).

De functie \(f(x)=\displaystyle\frac{1}{x^2+1}\) is continu, positief en dalend op \([0,\infty)\) en

\[\int_0^{\infty}\frac{1}{x^2+1}\,dx=\arctan(x)\bigg|_0^{\infty}=\frac{1}{2}\pi.\]

Dus: de integraal \(\displaystyle\int_0^{\infty}\frac{1}{x^2+1}\,dx\) is convergent, waaruit volgt dat de reeks \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n^2+1}\) ook convergent is.

Een reeks van de vorm \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^p}\) heet een \(\underline{\smash{p}}\)-reeks.

Het integraalkenmerk kan worden gebruikt om de volgende stelling te bewijzen:

Stelling: Een \(p\)-reeks is convergent als \(p>1\) en divergent als \(p\le 1\).

Dit is gebaseerd op het fiet dat \(\displaystyle\int_1^{\infty}\frac{1}{x^p}\,dx\) convergent is als \(p>1\) en divergent als \(p\leq1\).

Stewart §11.3, Voorbeeld 4
Beschouw de reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{\ln(n)}{n}\).

Merk eerst op dat de functie \(f(x)=\displaystyle\frac{\ln(x)}{x}\) positief en continu is voor \(x > 1\). Verder geldt:

\[f'(x)=\frac{\frac{1}{x}\cdot x-\ln(x)}{x^2}=\frac{1-\ln(x)}{x^2} < 0\quad\text{voor}\quad x > e.\]

Hieruit volgt dat de functie \(f\) dalend is voor \(x > e\) en dat we het integraalkenmerk kunnen toepassen:

\[\int_1^{\infty}\frac{\ln(x)}{x}\,dx=\frac{1}{2}(\ln(x))^2\bigg|_1^{\infty}=\infty.\]

Hieruit volgt dat de reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{\ln(n)}{n}\) divergent is.

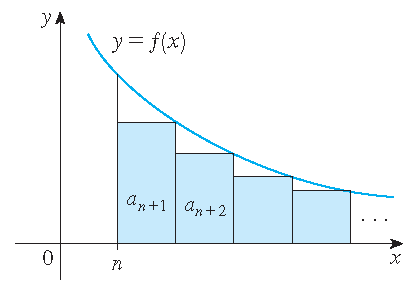
Benadering van de som van een reeks

Stelling: Neem aan dat \(f(k)=a_k\), waarbij \(f\) een continue, positieve en dalende functie is voor \(x\geq n\) en dat \(\displaystyle\sum a_n\) convergent is. Als \(s\) de som van de reeks is en \(s_n=\displaystyle\sum_{k=1}^na_k\) is de \(n^{\text{e}}\) partiële som met restterm \(R_n=s-s_n\), dan geldt

\[\int_{n+1}^{\infty}f(x)\,dx\leq R_n\leq\int_n^{\infty}f(x)\,dx.\]

---

Laatst gewijzigd op 15 maart 2021