Calculus – Sequences and series – The integral test

We have already seen: the harmonic series \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\) is divergent.

Proof based on the integral test:


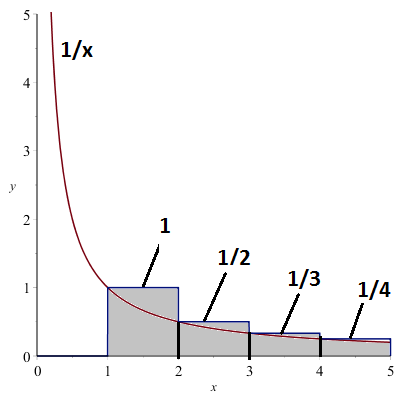
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots > \int_1^{\infty}\frac{1}{x}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\infty\).

Similarly we have: the series \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}\) is convergent.

Proof based on the integral test:


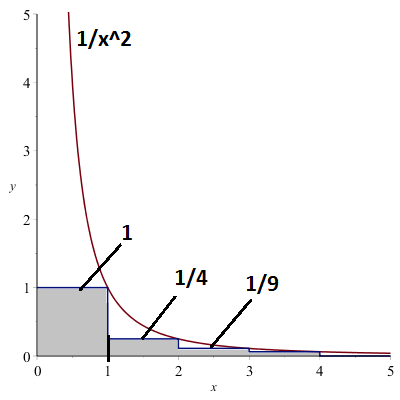
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\cdots < \int_1^{\infty}\frac{1}{x^2}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x^2}\,dx=1\).

The integral test

Theorem: Suppose \(f\) is a continuous, positive and decreasing function on \([1,\infty)\) and let \(a_n=f(n)\). Then we have:

\[\sum_{n=1}^{\infty}a_n\;\;\text{is convergent}\quad\Longleftrightarrow\quad\int_1^{\infty}f(x)\,dx\;\;\text{is convergent.}\]

In other words:

1. If \(\displaystyle\int_1^{\infty}f(x)\,dx\) is convergent, then \(\displaystyle\sum_{n=1}^{\infty}a_n\) is convergent.


2. If \(\displaystyle\int_1^{\infty}f(x)\,dx\) is divergent, then \(\displaystyle\sum_{n=1}^{\infty}a_n\) is divergent.

Note that it is not necessary to start at \(1\) (both for the series and the integral) and that \(f\) should be ultimately decreasing.

Stewart §11.3, Example 1
Consider the series \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n^2+1}\).

The function \(f(x)=\displaystyle\frac{1}{x^2+1}\) is continuous, positive and decreasing on \([0,\infty)\) and

\[\int_0^{\infty}\frac{1}{x^2+1}\,dx=\arctan(x)\bigg|_0^{\infty}=\frac{1}{2}\pi.\]

Hence: the integral \(\displaystyle\int_0^{\infty}\frac{1}{x^2+1}\,dx\) is convergent, which implies that the series \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n^2+1}\) is convergent as well.

A series of the form \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^p}\) is called a \(\underline{\smash{p}}\)-series.

The integral test can be used to prove the following theorem:

Theorem: A \(p\)-series is convergent if \(p>1\) and divergent if \(p\le 1\).

This is based on the fact that \(\displaystyle\int_1^{\infty}\frac{1}{x^p}\,dx\) is convergent if \(p>1\) and divergent if \(p\leq1\).

Stewart §11.3, Example 4
Consider the series \(\displaystyle\sum_{n=1}^{\infty}\frac{\ln(n)}{n}\).

First note that the function \(f(x)=\displaystyle\frac{\ln(x)}{x}\) is positive and continuous for \(x > 1\). Further we have:

\[f'(x)=\frac{\frac{1}{x}\cdot x-\ln(x)}{x^2}=\frac{1-\ln(x)}{x^2} < 0\quad\text{for}\quad x > e.\]

This implies that the function \(f\) is decreasing for \(x > e\) and that we can apply the integral test:

\[\int_1^{\infty}\frac{\ln(x)}{x}\,dx=\frac{1}{2}(\ln(x))^2\bigg|_1^{\infty}=\infty.\]

This implies that the series \(\displaystyle\sum_{n=1}^{\infty}\frac{\ln(n)}{n}\) is divergent.

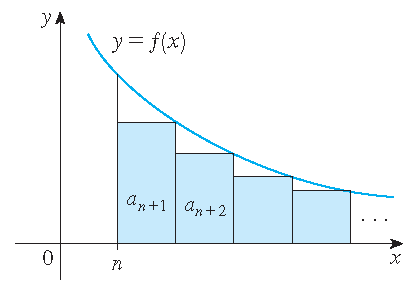
Estimating the sum of a series

Theorem: Suppose that \(f(k)=a_k\), where \(f\) is a continuous, positive and decreasing function for \(x\geq n\) and \(\displaystyle\sum a_n\) is convergent. If \(s\) is the sum of the series and \(s_n=\displaystyle\sum_{k=1}^na_k\) is the \(n^{\text{th}}\) partial sum with remainder \(R_n=s-s_n\), then

\[\int_{n+1}^{\infty}f(x)\,dx\leq R_n\leq\int_n^{\infty}f(x)\,dx.\]

---

Last modified on March 15, 2021