Calculus – Sequences and series – Taylor series

We start by supposing that \(f\) is a infinitely differentiable function that can be represented by a power series

\[f(x)=c_0+c_1(x-a)+c_2(x-a)^2+c_3(x-a)^3+c_4(x-a)^4+\cdots=\sum_{n=0}^{\infty}c_n(x-a)^n,\quad|x-a| < R\]

with positive radius of convergence \(R\). Then we have

\[f'(x)=c_1+2c_2(x-a)+3c_3(x-a)^2+4c_4(x-a)^3+5c_5(x-a)^4+\cdots=\sum_{n=1}^{\infty}n(x-a)^{n-1},\quad|x-a| < R,\] \[f''(x)=2c_2+2\cdot3c_3(x-a)+3\cdot4c_4(x-a)^2+4\cdot5c_5(x-a)^3+\cdots=\sum_{n=2}^{\infty}n(n-1)(x-a)^{n-2},\quad|x-a| < R,\] \[f^{(3)}(x)=2\cdot3c_3+2\cdot3\cdot4c_4(x-a)+3\cdot4\cdot5c_5(x-a)^2+4\cdot5\cdot6c_6(x-a)^3+\cdots=\sum_{n=3}^{\infty}n(n-1)(n-2)(x-a)^{n-3},\quad|x-a| < R,\]

and so on. Since all these power series converge at least at \(a\) we substitute \(x=a\) to obtain that

\[f(a)=c_0,\quad f'(a)=c_1,\quad f''(a)=2c_2,\quad f^{(3)}(a)=2\cdot3c_3,\quad\ldots\quad\Longrightarrow\quad f^{(n)}(a)=1\cdot2\cdot3\cdot4\cdots nc_n=n!c_n,\quad n=1,2,3,\ldots.\]

Theorem: If \(f\) has a power series representation (expansion) at \(a\), that is, if for some \(R>0\)

\[f(x)=\sum_{n=0}^{\infty}c_n(x-a)^n,\quad|x-a| < R,\]

then the coefficients are given by the formula

\[c_n=\frac{f^{(n)}(a)}{n!},\quad n=0,1,2,\ldots.\]

Definition:The series

\[\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots\]

is called the Taylor series of the function \(f\) at \(a\). The special case with \(a=0\)

\[\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f^{(3)}(0)}{3!}x^3+\cdots\]

is sometimes called the Maclaurin series of \(f\).

Examples:

1) For \(f(x)=e^x\) we have: \(f^{(n)}(x)=e^x\) for \(n=0,1,2,\ldots\). Hence: \(f^{(n)}(0)=1\) for \(n=0,1,2,\ldots\). This implies that

\[e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\frac{1}{24}x^4+\frac{1}{120}x^5+\cdots.\]

In order to find the radius of convergence, we apply the ratio test: for \(x\neq0\) let \(a_n=\displaystyle\frac{x^n}{n!}\), then we have

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{x^{n+1}}{(n+1)!}\cdot\frac{n!}{x^n}\right| =\lim\limits_{n\to\infty}\frac{|x|}{n+1}=0.\]

This implies that the Taylor series converges for all \(x\in\mathbb{R}\), so the radius of convergence is \(R=\infty\).

2) For \(f(x)=\sin(x)\) we have: \(f'(x)=\cos(x)\), \(f''(x)=-\sin(x)\), \(f^{(3)}(x)=-\cos(x)\), \(f^{(4)}(x)=\sin(x)=f(x)\) and so on. Hence: \(f(0)=0\), \(f'(0)=1\), \(f''(0)=0\), \(f^{(3)}(0)=-1\), \(f^{(4)}(0)=1=f(0)\) and so on. This implies that

\[\sin(x)=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1}=x-\frac{1}{6}x^3+\frac{1}{120}x^5-\frac{1}{5040}x^7+\cdots.\]

In order to find the radius of convergence, we apply the ratio test: for \(x\neq0\) let \(a_n=\displaystyle\frac{(-1)^n}{(2n+1)!}x^{2n+1}\), then we have

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(-1)^{n+1}x^{2n+3}}{(2n+3)!}\cdot\frac{(2n+1)!}{(-1)^nx^{2n+1}}\right| =\lim\limits_{n\to\infty}\frac{x^2}{(2n+2)(2n+3)}=0.\]

This implies that the Taylor series converges for all \(x\in\mathbb{R}\), so the radius of convergence is \(R=\infty\). Similarly we obtain that

\[\cos(x)=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}x^{2n}=1-\frac{1}{2}x^2+\frac{1}{24}x^4-\frac{1}{720}x^6+\cdots.\]

In order to find the radius of convergence, we apply the ratio test: for \(x\neq0\) let \(a_n=\displaystyle\frac{(-1)^n}{(2n)!}x^{2n}\), then we have

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(-1)^{n+1}x^{2n+2}}{(2n+2)!}\cdot\frac{(2n)!}{(-1)^nx^{2n}}\right| =\lim\limits_{n\to\infty}\frac{x^2}{(2n+1)(2n+2)}=0.\]

This implies that the Taylor series converges for all \(x\in\mathbb{R}\), so the radius of convergence is \(R=\infty\).

Definition: If \(f\) is a function for which the Taylor series at \(a\) exists, then for \(n=0,1,2,\ldots\)

\[T_n(x)=\sum_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a)^k=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n\]

is called the \(n^{\text{th}}\)-degree Taylor polynomial of \(f\) at \(a\).

As an example, the function \(f(x)=e^x\) and its Taylor polynomials \(T_1(x)=1+x\), \(T_2(x)=1+x+\frac{1}{2}x^2\) and \(T_3(x)=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3\):

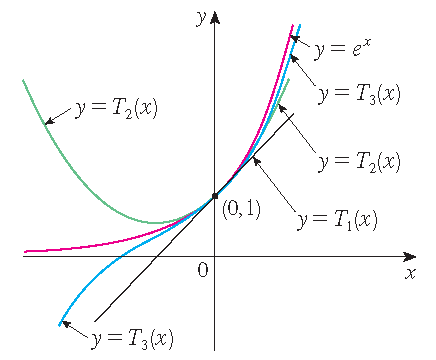
Applications:

1) Using \(e^x=1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\cdots\) for all \(x\in\mathbb{R}\) we find that

\[\lim\limits_{x\to 0}\frac{e^x-1-x}{x^2}=\lim\limits_{x\to 0}\frac{1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\cdots-1-x}{x^2} =\lim\limits_{x\to 0}\frac{\frac{1}{2}x^2+\frac{1}{6}x^3+\cdots}{x^2}=\lim\limits_{x\to 0}\left(\frac{1}{2}+\frac{1}{6}x+\cdots\right) =\frac{1}{2}+0+0=\frac{1}{2}.\]

2) Using \(\cos(x)=1-\frac{1}{2}x^2+\frac{1}{24}x^4-\frac{1}{720}x^6+\cdots\) for all \(x\in\mathbb{R}\) we find that

\begin{align*} \lim\limits_{x\to 0}\frac{\cos(x)-1+\frac{1}{2}x^2}{x^4}&=\lim\limits_{x\to 0}\frac{1-\frac{1}{2}x^2+\frac{1}{24}x^4-\frac{1}{720}x^6+\cdots-1+\frac{1}{2}x^2}{x^4} =\lim\limits_{x\to 0}\frac{\frac{1}{24}x^4-\frac{1}{720}x^6+\cdots}{x^4}\\[2.5mm] &=\lim\limits_{x\to 0}\left(\frac{1}{24}-\frac{1}{720}x^2+\cdots\right)=\frac{1}{24}-0+0=\frac{1}{24}. \end{align*}

3) Using \(\sin(x)=\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1}\) for all \(x\in\mathbb{R}\) we obtain that

\[\int_0^1x\sin(x^3)_\,dx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}\int_0^1x^{6n+4}\,dx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}\cdot\frac{1}{6n+5} =\frac{1}{5}-\frac{1}{66}+\frac{1}{2040}-\frac{1}{115920}+\cdots.\]

By taking more and more terms this leads to the approximations \(0.2\), \(0.184848\), \(0.185338\), \(0.185330\) and so on.

4) Using \(e^x=\displaystyle\sum_{n=0}^{\infty}\frac{x^n}{n!}\) for all \(x\in\mathbb{R}\) we obtain that

\[\int_0^{\frac{1}{2}}xe^{-x^4}\,dx=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}\int_0^{\frac{1}{2}}x^{4n+1}\,dx=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}\cdot\frac{(\frac{1}{2})^{4n+2}}{4n+2} =\frac{1}{8}-\frac{1}{384}+\frac{1}{20480}-\frac{1}{1376256}+\cdots.\]

By taking more and more terms this leads to the approximations \(0.125\), \(0.122396\), \(0.122445\), \(0.122444\) and so on.

---

Last modified on March 15, 2021