Calculus – Sequences and series – The Fibonacci sequence

The Fibonacci sequence \(1,1,2,3,5,8,13,21,34,55,89,\ldots\) is defined by \(F_{n+2}=F_n+F_{n+1}\) for \(n=1,2,3,\ldots\) with \(F_1=F_2=1\).

For computational reasons we use \(F_{n+2}=F_n+F_{n+1}\) for \(n=0,1,2,\ldots\) with \(F_0=0\) and \(F_1=1\) instead.

Question: What is \(F_{100}\) (for instance) or more general, what is \(F_n\) for arbitrary \(n\)?

The equation

\[F_{n+2}=F_n+F_{n+1}\quad\Longleftrightarrow\quad F_{n+2}-F_{n+1}-F_n=0\]

is called a difference equation. In this case a linear difference equation with constant coefficients. The theory of these linear difference equations with constant coefficients is similar to the theory of linear differential equations with constant coefficients. Try to find a solution of the form \(F_n=r^n\) for certain \(r\in\mathbb{R}\), then we have:

\[r^{n+2}-r^{n+1}-r^n=0\quad\Longleftrightarrow\quad r^n(r^2-r-1)=0.\]

If we assume that \(r\neq0\), then we have: \(r^2-r-1=0\). This is (also) called an auxiliary equation. This auxiliary equation has two (different) real solutions:

\[r^2-r-1=0\quad\Longrightarrow\quad r=\frac{1\pm\sqrt{5}}{2}.\]

Due to the linearity (the principle of superposition) it follows that

\[F_n=c_1\left(\frac{1+\sqrt{5}}{2}\right)^n+c_2\left(\frac{1-\sqrt{5}}{2}\right)^n,\quad n=0,1,2,\ldots\]

is the general solution of the second-order difference equation. Now we use the initial conditions \(F_0=0\) and \(F_1=1\) to find that

\[c_1+c_2=0\quad\text{and}\quad c_1\left(\frac{1+\sqrt{5}}{2}\right)+c_2\left(\frac{1-\sqrt{5}}{2}\right)=1.\]

Hence:

\[\left\{\begin{array}{l}c_1+c_2=0\\[2.5mm]c_1(1+\sqrt{5})+c_2(1-\sqrt{5})=2\end{array}\right.\quad\Longleftrightarrow\quad \left\{\begin{array}{l}c_1+c_2=0\\[2.5mm]c_1\sqrt{5}-c_2\sqrt{5}=2\end{array}\right.\]

which implies that \(c_1=\displaystyle\frac{1}{\sqrt{5}}\) and \(c_2=-\displaystyle\frac{1}{\sqrt{5}}\).

Hence we have

\[F_n=\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n-\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n =\frac{(1+\sqrt{5})^n-(1-\sqrt{5})^n}{2^n\sqrt{5}},\quad n=0,1,2,\ldots.\]

This formula is remarkable since all numbers in the Fibonacci sequence are integers. In this formula this is far from evident. However we have for instance:

\[F_{100}=\frac{(1+\sqrt{5})^{100}-(1-\sqrt{5})^{100}}{2^{100}\sqrt{5}}=354224848179261915075.\]

The number \(\varphi=\displaystyle\frac{1+\sqrt{5}}{2}\) is also known as the golden ratio. Now we have

\[F_n=\frac{\varphi^n-(1-\varphi)^n}{\sqrt{5}},\quad n=0,1,2,\ldots.\]

The golden ratio \(\varphi=\displaystyle\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}\) often appears in nature:

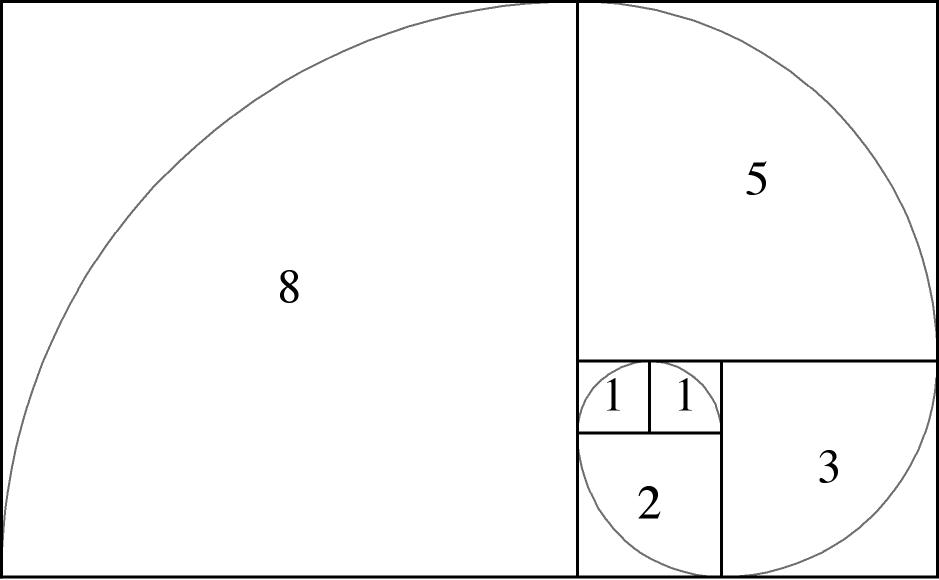
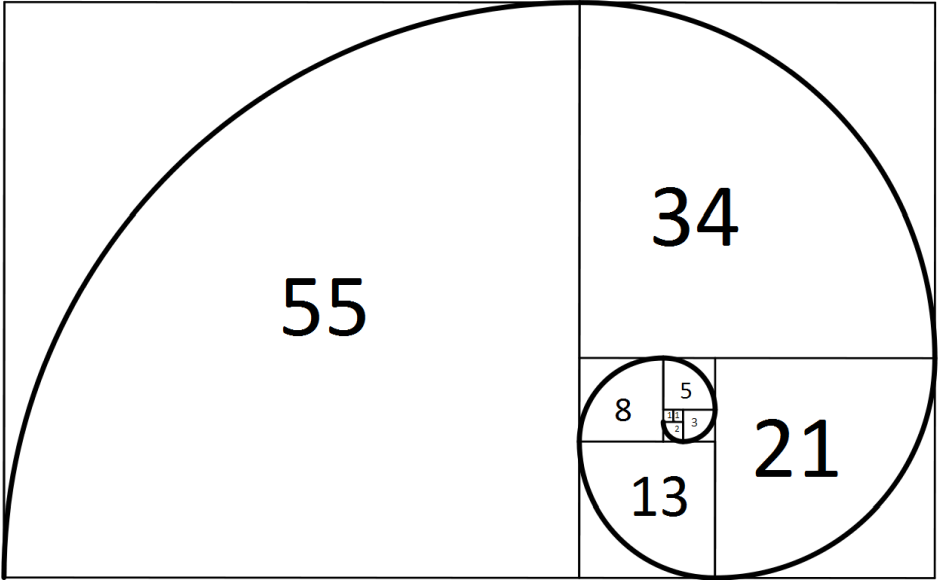
In order to prove that \(\displaystyle\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi\), we first conclude that the limit exists because \(\displaystyle\{\frac{F_{n+1}}{F_n}\}\) is an increasing sequence which is bounded:

\[1 < \frac{F_{n+1}}{F_n}=\frac{F_n+F_{n-1}}{F_n}=1+\frac{F_{n-1}}{F_n}<1+1=2,\quad n>3.\]

Then we have

\[1 < L=\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}=\lim\limits_{n\to\infty}\frac{F_n+F_{n-1}}{F_n}=1+\lim\limits_{n\to\infty}\frac{F_{n-1}}{F_n}=1+\frac{1}{L}.\]

Hence: \(1 < L < 2\) and \(L=1+\displaystyle\frac{1}{L}\) or \(L^2-L-1=0\), which implies that \(L=\displaystyle\frac{1+\sqrt{5}}{2}=\varphi\).

More results on Fibonacci numbers

Since \(F_{n+2}=F_n+F_{n+1}\) for \(n=1,2,3,\ldots\) with \(F_1=F_2=1\) we use the telescoping property to find that

\[\sum_{k=1}^nF_k=\sum_{k=1}^n\left(F_{k+2}-F_{k+1}\right)=F_{n+2}-F_{n+1}+F_{n+1}-F_n+\cdots+F_3-F_2=F_{n+2}-1.\]

Furthermore, applying partial fractions we obtain

\[\frac{1}{F_nF_{n+2}}=\frac{A}{F_n}+\frac{B}{F_{n+2}}=\frac{AF_{n+2}+BF_n}{F_nF_{n+2}} =\frac{A\left(F_n+F_{n+1}\right)+BF_n}{F_nF_{n+2}}=\frac{(A+B)F_n+AF_{n+1}}{F_nF_{n+2}}.\]

Note that this is satisfied for \(A=\displaystyle\frac{1}{F_{n+1}}\) and \(B=-\displaystyle\frac{1}{F_{n+1}}\), which implies that

\[\frac{1}{F_nF_{n+2}}=\frac{1}{F_nF_{n+1}}-\frac{1}{F_{n+1}F_{n+2}}.\]

Now we use the telescoping property to find that

\[\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}=\lim\limits_{N\to\infty}\sum_{n=1}^N\left(\frac{1}{F_nF_{n+1}}-\frac{1}{F_{n+1}F_{n+2}}\right) =\lim\limits_{N\to\infty}\left(\frac{1}{F_1F_2}-\frac{1}{F_{N+1}F_{N+2}}\right)=1\]

and

\[\sum_{n=1}^{\infty}\frac{F_{n+1}}{F_nF_{n+2}}=\lim\limits_{N\to\infty}\sum_{n=1}^{\infty}\left(\frac{1}{F_n}-\frac{1}{F_{n+2}}\right) =\lim\limits_{N\to\infty}\left(\frac{1}{F_1}+\frac{1}{F_2}-\frac{1}{F_{N+1}}-\frac{1}{F_{N+2}}\right)=1+1=2.\]

Similarly, we have

\begin{align*} \frac{1}{F_nF_{n+4}}&=\frac{A}{F_n}+\frac{B}{F_{n+4}}=\frac{AF_{n+4}+BF_n}{F_nF_{n+4}}=\frac{A\left(F_{n+2}+F_{n+3}\right)+BF_n}{F_nF_{n+4}}\\[2.5mm] &=\frac{A\left(F_{n+2}+F_{n+1}+F_{n+2}\right)+BF_n}{F_nF_{n+4}}=\frac{A\left(2F_{n+2}+F_{n+2}-F_n\right)+BF_n}{F_nF_{n+4}}\\[2.5mm] &=\frac{A\left(3F_{n+2}-F_n\right)+BF_n}{F_nF_{n+4}}=\frac{3AF_{n+2}+(B-A)F_n}{F_nF_{n+4}}\quad\Longrightarrow\quad A=B=\frac{1}{3F_{n+2}}. \end{align*}

This implies that

\begin{align*} \sum_{n=1}^{\infty}\frac{1}{F_nF_{n+4}}&=\sum_{n=1}^{\infty}\left(\frac{1}{3F_nF_{n+2}}+\frac{1}{3F_{n+2}F_{n+4}}\right)\\[2.5mm] &=\frac{1}{3}\left(\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}+\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}-\frac{1}{F_1F_3}-\frac{1}{F_2F_4}\right) =\frac{1}{3}\left(2-\frac{1}{2}-\frac{1}{3}\right)=\frac{7}{18}. \end{align*}

---

Last modified on March 15, 2021