Calculus – Sequences and series

Definition: A sequence \(\{a_n\}_{n=1}^{\infty}\) is an ordered list of numbers: \(a_1,a_2,a_3,\ldots\).

Adding the terms of this sequence \(\{a_n\}_{n=1}^{\infty}\) we get an expression of the form \(a_1+a_2+a_3+\cdots\), which is called an infinite series or just series and is denoted by \(\displaystyle\sum_{n=1}^{\infty}a_n\) or just \(\displaystyle\sum a_n\).

Given a series \(\displaystyle\sum_{n=1}^{\infty}a_n=a_1+a_2+a_3+\cdots\), let \(s_n\) denote its \(n^{\text{th}}\) partial sum: \(s_n=\displaystyle\sum_{k=1}^na_k=a_1+a_2+a_3+\cdots+a_n\).

The partial sums form a sequence \(\{s_n\}_{n=1}^{\infty}\). Now we consider \(\lim\limits_{n\to\infty}s_n\).

Definition: If the limit \(\lim\limits_{n\to\infty}s_n=s\) exists, then the series \(\displaystyle\sum a_n\) is called convergent and we write \(a_1+a_2+a_3+\cdots=s\) or \(\displaystyle\sum_{n=1}^{\infty}a_n=s\).

The number \(s\) is called the sum of the series. If the limit \(\lim\limits_{n\to\infty}s_n\) does not exist, then the series is called divergent.

Theorem: A geometric series \(\displaystyle\sum_{n=1}^{\infty}ar^{n-1}=a+ar+ar^2+\cdots\) with common ratio \(r\) is convergent if \(|r|<1\) and its sum is \(\displaystyle\frac{a}{1-r}\). If \(|r|\geq1\), the geometric series is divergent.

Examples:

1. \(\displaystyle\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots=\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1\),
2. \(\displaystyle\frac{1}{5}-\frac{2}{25}+\frac{4}{125}-\frac{8}{625}+\cdots=\frac{1}{5}\sum_{n=0}^{\infty}\left(-\frac{2}{5}\right)^n=\frac{1}{5}\cdot\frac{1}{1+\frac{2}{5}}=\frac{1}{5}\cdot\frac{5}{7}=\frac{1}{7}\).
3. \(\displaystyle0.111111\ldots=0.\overline{1}=\sum_{n=1}^{\infty}\left(\frac{1}{10}\right)^n=\frac{\frac{1}{10}}{1-\frac{1}{10}}=\frac{1}{9}\).

Telescoping series

An example of a telescoping series is \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n(n+1)}\).

Then the \(n^{\text{th}}\) partial sum is: \(s_n=\displaystyle\sum_{k=1}^n\frac{1}{k(k+1)}=\sum_{k=1}^n\left(\frac{1}{k}-\frac{1}{k+1}\right)\). Hence we have

\[s_n=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{n}-\frac{1}{n+1}=1-\frac{1}{n+1}.\]

Hence we have \(\lim\limits_{n\to\infty}s_n=1\). This implies that the series is convergent and that \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n(n+1)}=1\).

Another example is \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-1}\). Then we have:

\begin{align*} \sum_{k=2}^n\frac{1}{k^2-1}&=\sum_{k=2}^n\frac{1}{(k-1)(k+1)}=\frac{1}{2}\sum_{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k+1}\right)\\ &=\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+\frac{1}{4}-\frac{1}{6}+\cdots+\frac{1}{n-2}-\frac{1}{n}+\frac{1}{n-1}-\frac{1}{n+1}\right)\\ &=\frac{1}{2}\left(1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}\right). \end{align*}

This implies that the series converges and that \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-1} =\lim\limits_{n\to\infty}\frac{1}{2}\left(\frac{3}{2}-\frac{1}{n}-\frac{1}{n+1}\right)=\frac{3}{4}\).

A third example is \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{(n-1)(n+2)}\). Then we have:

\begin{align*} \sum_{k=2}^n\frac{1}{(k-1)(k+2)}&=\frac{1}{3}\sum_{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k+2}\right)\\ &=\frac{1}{3}\left(\frac{1}{1}-\frac{1}{4}+\frac{1}{2}-\frac{1}{5}+\frac{1}{3}-\frac{1}{6}+\frac{1}{4}-\frac{1}{7}+\cdots+\frac{1}{n-3}-\frac{1}{n}+\frac{1}{n-2}-\frac{1}{n+1}+\frac{1}{n-1}-\frac{1}{n+2}\right)\\ &=\frac{1}{3}\left(1+\frac{1}{2}+\frac{1}{3}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right). \end{align*}

This implies that the series converges and that \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{(n-1)(n+2)} =\lim\limits_{n\to\infty}\frac{1}{3}\left(\frac{11}{6}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right)=\frac{11}{18}\).

Theorem: If the series \(\displaystyle\sum a_n\) is convergent, then \(\lim\limits_{n\to\infty}a_n=0\).

Corollary: If \(\lim\limits_{n\to\infty}a_n\) does not exist or if \(\lim\limits_{n\to\infty}a_n\ne 0\), then the series \(\sum a_n\) is divergent.

However, if \(\lim\limits_{n\to\infty}a_n=0\), the series does not need to be convergent!

Example: The harmonic series \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\) is divergent.

Proof based on the integral test:


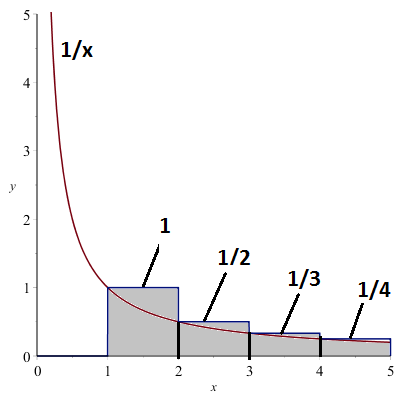
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots > \int_1^{\infty}\frac{1}{x}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\infty\).

---

Last modified on March 15, 2021