Analyse – Rijen en reeksen

Definitie: Een rij \(\{a_n\}_{n=1}^{\infty}\) is een geordende lijst van getallen: \(a_1,a_2,a_3,\ldots\).

Als we de termen van deze rij \(\{a_n\}_{n=1}^{\infty}\) bij elkaar optellen, dan krijgen we een uitdrukking van de vorm \(a_1+a_2+a_3+\cdots\); dit heet een oneindige reeks of kortweg reeks en wordt genoteerd als \(\displaystyle\sum_{n=1}^{\infty}a_n\) of kortweg \(\displaystyle\sum a_n\).

Gegeven een reeks \(\displaystyle\sum_{n=1}^{\infty}a_n=a_1+a_2+a_3+\cdots\), dan is \(s_n\) de \(n^{\text{e}}\) partiële som: \(s_n=\displaystyle\sum_{k=1}^na_k=a_1+a_2+a_3+\cdots+a_n\).

De partiële sommen vormen een rij \(\{s_n\}_{n=1}^{\infty}\). Beschouw nu \(\lim\limits_{n\to\infty}s_n\).

Definitie: Als de limiet \(\lim\limits_{n\to\infty}s_n=s\) bestaat, dan heet de reeks \(\displaystyle\sum a_n\) convergent en schrijven we \(a_1+a_2+a_3+\cdots=s\) of \(\displaystyle\sum_{n=1}^{\infty}a_n=s\).

Het getal \(s\) heet de som van de reeks. Als de limiet \(\lim\limits_{n\to\infty}s_n\) niet bestaat, dan heet de reeks divergent.

Stelling: Een meetkundige reeks \(\displaystyle\sum_{n=1}^{\infty}ar^{n-1}=a+ar+ar^2+\cdots\) met reden \(r\) is convergent als \(|r|<1\) en de som is dan \(\displaystyle\frac{a}{1-r}\). Als \(|r|\geq1\), dan is de meetkundige reeks divergent.

Voorbeelden:

1. \(\displaystyle\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots=\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1\),
2. \(\displaystyle\frac{1}{5}-\frac{2}{25}+\frac{4}{125}-\frac{8}{625}+\cdots=\frac{1}{5}\sum_{n=0}^{\infty}\left(-\frac{2}{5}\right)^n=\frac{1}{5}\cdot\frac{1}{1+\frac{2}{5}}=\frac{1}{5}\cdot\frac{5}{7}=\frac{1}{7}\).
3. \(\displaystyle0.111111\ldots=0.\overline{1}=\sum_{n=1}^{\infty}\left(\frac{1}{10}\right)^n=\frac{\frac{1}{10}}{1-\frac{1}{10}}=\frac{1}{9}\).

Telescopische reeksen

Een voorbeeld van een telescopische reeks is \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n(n+1)}\).

De \(n^{\text{e}}\) partiële som is dan: \(s_n=\displaystyle\sum_{k=1}^n\frac{1}{k(k+1)}=\sum_{k=1}^n\left(\frac{1}{k}-\frac{1}{k+1}\right)\). Dan geldt

\[s_n=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{n}-\frac{1}{n+1}=1-\frac{1}{n+1}.\]

Dus geldt dat \(\lim\limits_{n\to\infty}s_n=1\). Hieruit volgt dat de reeks convergent is en dat \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n(n+1)}=1\).

Een ander voorbeeld is \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-1}\). Dan geldt:

\begin{align*} \sum_{k=2}^n\frac{1}{k^2-1}&=\sum_{k=2}^n\frac{1}{(k-1)(k+1)}=\frac{1}{2}\sum_{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k+1}\right)\\ &=\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+\frac{1}{4}-\frac{1}{6}+\cdots+\frac{1}{n-2}-\frac{1}{n}+\frac{1}{n-1}-\frac{1}{n+1}\right)\\ &=\frac{1}{2}\left(1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}\right). \end{align*}

Hieruit volgt dat de reeks convergeert en dat \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-1} =\lim\limits_{n\to\infty}\frac{1}{2}\left(\frac{3}{2}-\frac{1}{n}-\frac{1}{n+1}\right)=\frac{3}{4}\).

Een derde voorbeeld is \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{(n-1)(n+2)}\). Dan geldt:

\begin{align*} \sum_{k=2}^n\frac{1}{(k-1)(k+2)}&=\frac{1}{3}\sum_{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k+2}\right)\\ &=\frac{1}{3}\left(\frac{1}{1}-\frac{1}{4}+\frac{1}{2}-\frac{1}{5}+\frac{1}{3}-\frac{1}{6}+\frac{1}{4}-\frac{1}{7}+\cdots+\frac{1}{n-3}-\frac{1}{n}+\frac{1}{n-2}-\frac{1}{n+1}+\frac{1}{n-1}-\frac{1}{n+2}\right)\\ &=\frac{1}{3}\left(1+\frac{1}{2}+\frac{1}{3}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right). \end{align*}

Hieruit volgt dat de reeks convergeert en dat \(\displaystyle\sum_{n=2}^{\infty}\frac{1}{(n-1)(n+2)} =\lim\limits_{n\to\infty}\frac{1}{3}\left(\frac{11}{6}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right)=\frac{11}{18}\).

Stelling: Als de reeks \(\displaystyle\sum a_n\) convergent is, dan is \(\lim\limits_{n\to\infty}a_n=0\).

Gevolg: Als \(\lim\limits_{n\to\infty}a_n\) niet bestaat of als \(\lim\limits_{n\to\infty}a_n\ne 0\), dan is de reeks \(\sum a_n\) is divergent.

Echter, als \(\lim\limits_{n\to\infty}a_n=0\), dan hoeft de reeks niet convergent te zijn!

Voorbeeld: De harmonische reeks \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\) is divergent.

Bewijs gebaseerd op het integraalkenmerk:


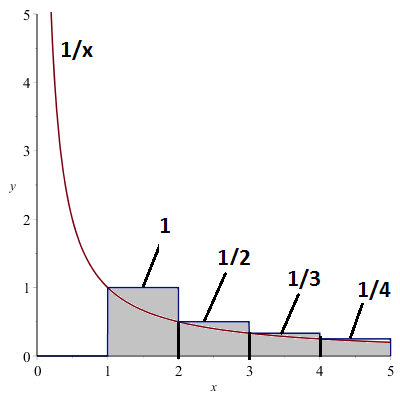
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots > \int_1^{\infty}\frac{1}{x}\,dx\)


\(\displaystyle\int_1^{\infty}\frac{1}{x}\,dx=\infty\).

---

Laatst gewijzigd op 15 maart 2021