Analyse – Rijen en reeksen – Alternerende reeksen

Een alternerende reeks is een reeks waarvan de termen afwisselend positief en negatief zijn.

Voorbeelden:

1. \(\quad\displaystyle1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\),


2. \(\quad\displaystyle-\frac{1}{2}+\frac{2}{3}-\frac{3}{4}+\frac{4}{5}-\frac{5}{6}+\cdots=\sum_{n=1}^{\infty}(-1)^n\frac{n}{n+1}\).

Stelling: Als de alternerende reeks \(\displaystyle\sum_{n=1}^{\infty}(-1)^{n-1}b_n\) met \(b_n > 0\) voldoet aan

1. \(b_{n+1}\leq b_n\) voor alle \(n\),


2. \(\lim\limits_{n\to\infty}b_n=0\),

dan convergeert de reeks.

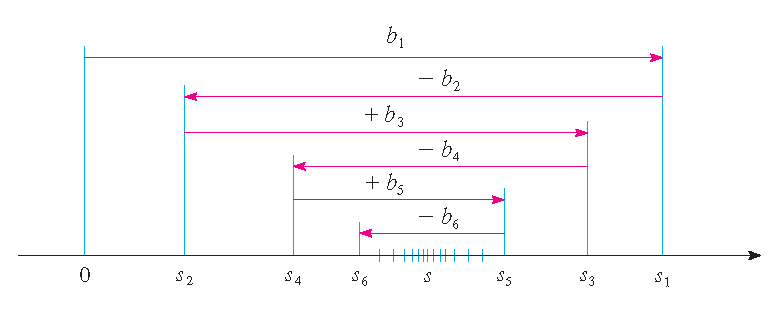
Bewijs:
We bekijken eerst de even partiële sommen \(s_2=b_1-b_2\geq0\), \(s_4=s_2+(b_3-b_4)\geq s_2\) enzovoort. Algemeen:

\[s_{2n+2}=s_{2n}+(b_{2n+1}-b_{2n+2})\geq s_{2n}\quad\text{voor}\quad n=1,2,3,\ldots.\]

Dus:

\[0\leq s_2\leq s_4\leq s_6\leq \cdots.\]

Maar er geldt ook:

\[s_{2n}=b_1-(b_2-b_3)-(b_4-b_5)-\cdots-(b_{2n-2}-b_{2n-1})-b_{2n}\leq b_1.\]

De rij \(\{s_{2n}\}\) van even partiële sommen is dus stijgend en naar boven begrensd en dus convergent. Zeg: \(\lim\limits_{n\to\infty}s_{2n}=s\). Dan volgt dat

\[\lim\limits_{n\to\infty}s_{2n+1}=\lim\limits_{n\to\infty}(s_{2n}+b_{2n+1})=\lim\limits_{n\to\infty}s_{2n}+\lim\limits_{n\to\infty}b_{2n+1}=s+0=s.\]

Omdat zowel de rij van even als de rij van oneven partiële sommen convergeert naar \(s\), concluderen we dat \(\lim\limits_{n\to\infty}s_n=s\) en dat betekent dat de reeks convergeert.

Voorbeelden:

1) De reeks \(\displaystyle1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\) is convergent, want: \(\displaystyle\frac{1}{n+1}\leq\frac{1}{n}\) voor alle \(n\) en \(\lim\limits_{n\to\infty}\displaystyle\frac{1}{n}=0\).

2) De reeks \(\displaystyle\sum_{n=1}^{\infty}(-1)^n\frac{3n}{4n+1}\) is divergent, want: \(\displaystyle\lim\limits_{n\to\infty}\frac{3n}{4n+1}=\lim\limits_{n\to\infty}\frac{3}{4+\frac{1}{n}}=\frac{3}{4}\neq0\). Hieruit volgt dat de limiet van de algemene term niet bestaat (en dus niet naar nul gaat).

3) De reeks \(\displaystyle\sum_{n=1}^{\infty}(-1)^{n-1}\frac{n^2}{n^3+1}\) is convergent, want: \(b_n=\displaystyle\frac{n^2}{n^3+1}=f(n)\) met \(f(x)=\displaystyle\frac{x^2}{x^3+1}\) en dus

\[f'(x)=\frac{2x(x^3+1)-3x^4}{(x^3+1)^2}=\frac{x(2-x^3)}{(x^3+1)^2}<0\quad\text{voor}\quad x>1.\]

Hieruit volgt dat \(b_{n+1}\leq b_n\) voor \(n\geq2\). Verder geldt: \(\displaystyle\lim\limits_{n\to\infty}b_n=\lim\limits_{n\to\infty}\frac{n^2}{n^3+1} =\lim\limits_{n\to\infty}\frac{\frac{1}{n}}{1+\frac{1}{n^3}}=0\).

Benadering van de som van een reeks

Stelling: Laat \(\displaystyle\sum(-1)^{n-1}b_n\) een alternerende reeks zijn met \(b_n>0\), \(b_{n+1}\leq b_n\) voor alle \(n\) en \(\displaystyle\lim\limits_{n\to\infty}b_n=0\). Als \(s_n\) de \(n^{\text{e}}\) partiële som van de reeks is en \(s=\lim\limits_{n\to\infty}s_n\), dan geldt voor de restterm \(R_n\): \(|R_n|=|s-s_n|\leq b_{n+1}\).

---

Laatst gewijzigd op 15 maart 2021