Analyse – Rijen en reeksen – De rij van Fibonacci

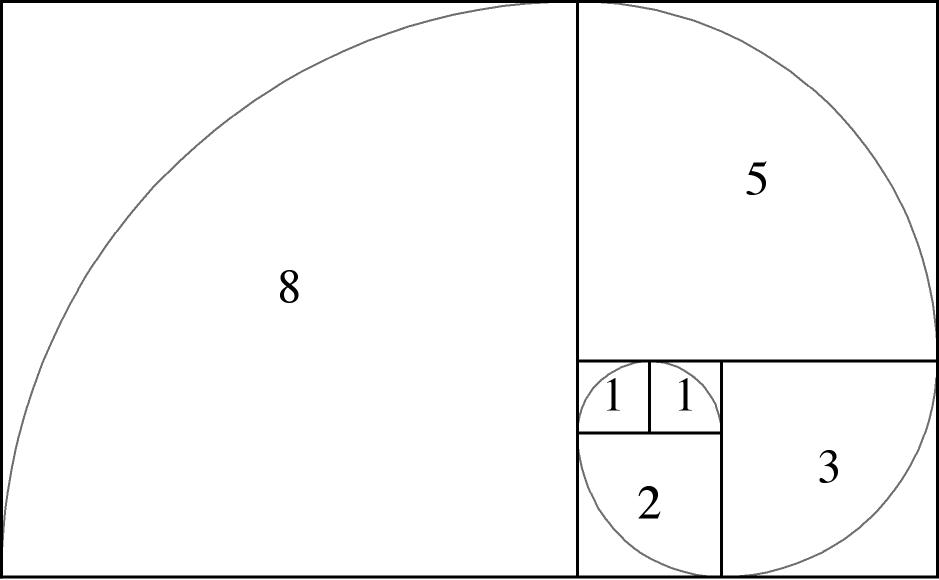
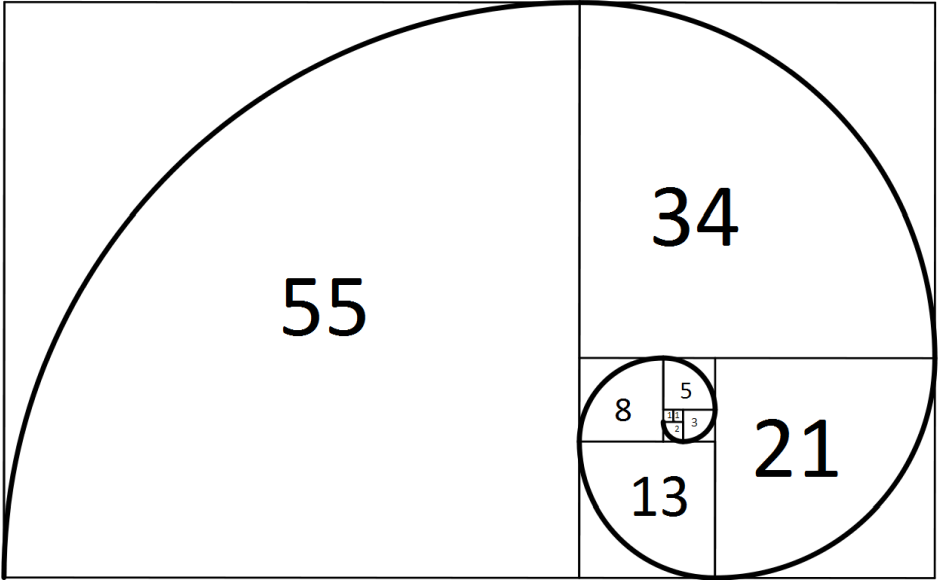
De rij van Fibonacci \(1,1,2,3,5,8,13,21,34,55,89,\ldots\) wordt gedefinieerd door \(F_{n+2}=F_n+F_{n+1}\) voor \(n=1,2,3,\ldots\) met \(F_1=F_2=1\).

Voor het gemak gebruiken we echter \(F_{n+2}=F_n+F_{n+1}\) voor \(n=0,1,2,\ldots\) met \(F_0=0\) en \(F_1=1\).

Vraag: Wat is \(F_{100}\) (bijvoorbeeld) of meer algemeen, wat is \(F_n\) voor willekeurige \(n\)?

De vergelijking

\[F_{n+2}=F_n+F_{n+1}\quad\Longleftrightarrow\quad F_{n+2}-F_{n+1}-F_n=0\]

heet een differentievergelijking. In dit geval een lineaire differentievergelijking met constante coëfficiënten. De theorie van deze lineaire differentievergelijkingen met constante coëfficiënten is vergelijkbaar met de theorie van lineaire differentiaalvergelijkingen met constante coëfficiënten. Probeer een oplossing van de vorm \(F_n=r^n\) voor zekere \(r\in\mathbb{R}\), dan volgt:

\[r^{n+2}-r^{n+1}-r^n=0\quad\Longleftrightarrow\quad r^n(r^2-r-1)=0.\]

Als we aannemen dat \(r\neq0\), dan volgt: \(r^2-r-1=0\). Dit heet (ook) een karakteristieke vergelijking. Deze karakteristieke vergelijking heeft twee (verschillende) reële oplossingen:

\[r^2-r-1=0\quad\Longrightarrow\quad r=\frac{1\pm\sqrt{5}}{2}.\]

Vanwege de lineariteit (het superpositieprincipe) volgt nu dat

\[F_n=c_1\left(\frac{1+\sqrt{5}}{2}\right)^n+c_2\left(\frac{1-\sqrt{5}}{2}\right)^n,\quad n=0,1,2,\ldots\]

de algemene oplossing is van de tweede orde differentievergelijking. Uit de beginvoorwaarden \(F_0=0\) en \(F_1=1\) volgt nu dat

\[c_1+c_2=0\quad\text{en}\quad c_1\left(\frac{1+\sqrt{5}}{2}\right)+c_2\left(\frac{1-\sqrt{5}}{2}\right)=1.\]

Dus:

\[\left\{\begin{array}{l}c_1+c_2=0\\[2.5mm]c_1(1+\sqrt{5})+c_2(1-\sqrt{5})=2\end{array}\right.\quad\Longleftrightarrow\quad \left\{\begin{array}{l}c_1+c_2=0\\[2.5mm]c_1\sqrt{5}-c_2\sqrt{5}=2\end{array}\right.\]

en hieruit volgt dat \(c_1=\displaystyle\frac{1}{\sqrt{5}}\) en \(c_2=-\displaystyle\frac{1}{\sqrt{5}}\).

Dus geldt dat

\[F_n=\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n-\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n =\frac{(1+\sqrt{5})^n-(1-\sqrt{5})^n}{2^n\sqrt{5}},\quad n=0,1,2,\ldots.\]

Deze formule is opmerkelijk omdat alle getallen in de rij van Fibonacci gehele getallen zijn. In deze formule is dat echter verre van evident. Er geldt echter bijvoorbeeld:

\[F_{100}=\frac{(1+\sqrt{5})^{100}-(1-\sqrt{5})^{100}}{2^{100}\sqrt{5}}=354224848179261915075.\]

Het getal \(\varphi=\displaystyle\frac{1+\sqrt{5}}{2}\) staat ook bekend als de gulden snede. Nu geldt dat

\[F_n=\frac{\varphi^n-(1-\varphi)^n}{\sqrt{5}},\quad n=0,1,2,\ldots.\]

De gulden snede \(\varphi=\displaystyle\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}\) komt vaak voor in de natuur:

Om aan te tonen dat \(\displaystyle\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi\), concluderen we eerst dat de limiet bestaat omdat \(\displaystyle\{\frac{F_{n+1}}{F_n}\}\) een stijgende rij is, die begrensd is:

\[1 < \frac{F_{n+1}}{F_n}=\frac{F_n+F_{n-1}}{F_n}=1+\frac{F_{n-1}}{F_n}<1+1=2,\quad n>3.\]

Dan geldt

\[1 < L=\lim\limits_{n\to\infty}\frac{F_{n+1}}{F_n}=\lim\limits_{n\to\infty}\frac{F_n+F_{n-1}}{F_n}=1+\lim\limits_{n\to\infty}\frac{F_{n-1}}{F_n}=1+\frac{1}{L}.\]

Dus: \(1 < L < 2\) en \(L=1+\displaystyle\frac{1}{L}\) of \(L^2-L-1=0\), waaruit volgt dat \(L=\displaystyle\frac{1+\sqrt{5}}{2}=\varphi\).

Meer resulaten over Fibonaccigetallen

Omdat \(F_{n+2}=F_n+F_{n+1}\) voor \(n=1,2,3,\ldots\) met \(F_1=F_2=1\) volgt uit de telescopische eigenschap dat

\[\sum_{k=1}^nF_k=\sum_{k=1}^n\left(F_{k+2}-F_{k+1}\right)=F_{n+2}-F_{n+1}+F_{n+1}-F_n+\cdots+F_3-F_2=F_{n+2}-1.\]

Verder leidt de toepassing van breuksplitsing tot

\[\frac{1}{F_nF_{n+2}}=\frac{A}{F_n}+\frac{B}{F_{n+2}}=\frac{AF_{n+2}+BF_n}{F_nF_{n+2}} =\frac{A\left(F_n+F_{n+1}\right)+BF_n}{F_nF_{n+2}}=\frac{(A+B)F_n+AF_{n+1}}{F_nF_{n+2}}.\]

Merk op dat hieraan wordt voldaan door \(A=\displaystyle\frac{1}{F_{n+1}}\) en \(B=-\displaystyle\frac{1}{F_{n+1}}\), waaruit volgt dat

\[\frac{1}{F_nF_{n+2}}=\frac{1}{F_nF_{n+1}}-\frac{1}{F_{n+1}F_{n+2}}.\]

Uit de telescopische eigenschap volgt dan dat

\[\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}=\lim\limits_{N\to\infty}\sum_{n=1}^N\left(\frac{1}{F_nF_{n+1}}-\frac{1}{F_{n+1}F_{n+2}}\right) =\lim\limits_{N\to\infty}\left(\frac{1}{F_1F_2}-\frac{1}{F_{N+1}F_{N+2}}\right)=1\]

en

\[\sum_{n=1}^{\infty}\frac{F_{n+1}}{F_nF_{n+2}}=\lim\limits_{N\to\infty}\sum_{n=1}^{\infty}\left(\frac{1}{F_n}-\frac{1}{F_{n+2}}\right) =\lim\limits_{N\to\infty}\left(\frac{1}{F_1}+\frac{1}{F_2}-\frac{1}{F_{N+1}}-\frac{1}{F_{N+2}}\right)=1+1=2.\]

Evenzo geldt dat

\begin{align*} \frac{1}{F_nF_{n+4}}&=\frac{A}{F_n}+\frac{B}{F_{n+4}}=\frac{AF_{n+4}+BF_n}{F_nF_{n+4}}=\frac{A\left(F_{n+2}+F_{n+3}\right)+BF_n}{F_nF_{n+4}}\\[2.5mm] &=\frac{A\left(F_{n+2}+F_{n+1}+F_{n+2}\right)+BF_n}{F_nF_{n+4}}=\frac{A\left(2F_{n+2}+F_{n+2}-F_n\right)+BF_n}{F_nF_{n+4}}\\[2.5mm] &=\frac{A\left(3F_{n+2}-F_n\right)+BF_n}{F_nF_{n+4}}=\frac{3AF_{n+2}+(B-A)F_n}{F_nF_{n+4}}\quad\Longrightarrow\quad A=B=\frac{1}{3F_{n+2}}. \end{align*}

Hieruit volgt dat

\begin{align*} \sum_{n=1}^{\infty}\frac{1}{F_nF_{n+4}}&=\sum_{n=1}^{\infty}\left(\frac{1}{3F_nF_{n+2}}+\frac{1}{3F_{n+2}F_{n+4}}\right)\\[2.5mm] &=\frac{1}{3}\left(\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}+\sum_{n=1}^{\infty}\frac{1}{F_nF_{n+2}}-\frac{1}{F_1F_3}-\frac{1}{F_2F_4}\right) =\frac{1}{3}\left(2-\frac{1}{2}-\frac{1}{3}\right)=\frac{7}{18}. \end{align*}

---

Laatst gewijzigd op 15 maart 2021