Calculus – Sequences and series – Power series

Definition: A series of the form

\[\sum_{n=0}^{\infty}c_nx^n=c_0+c_1x+c_2x^2+\cdots\]

is called a power series in \(x\). The constants \(\{c_n\}_{n=0}^{\infty}\) are called the coefficients of the power series.

More generally, a series of the form

\[\sum_{n=0}^{\infty}c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+\cdots\]

is called a power series in \(x-a\) or a power series centered a \(x=a\) or a power series about \(a\).

Examples:

1) The power series \(\displaystyle\sum_{n=0}^{\infty}x^n\) is a geometric series with common ratio \(x\). Hence, this power series is absolutely convergent if \(|x| < 1\) and is divergent if \(|x|\geq1\). Moreover, for \(|x| < 1\) the sum of the series is \(\displaystyle\frac{1}{1-x}\).

2) The series \(\displaystyle\sum_{n=1}^{\infty}\frac{(x-2)^{n-1}}{n}\) is a power series about \(2\). Note that the series converges for \(x=2\) (with sum \(1\)). For \(x\neq2\) we might apply the ratio test: let \(a_n=\displaystyle\frac{(x-2)^{n-1}}{n}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(x-2)^n}{n+1}\cdot\frac{n}{(x-2)^{n-1}}\right| =\lim\limits_{n\to\infty}\frac{n}{n+1}\cdot|x-2|=|x-2|.\]

Hence, the series is absolutely convergent if \(|x-2| < 1\) and is divergent if \(|x-2| > 1\). The ratio test is inconclusive if \(|x-2|=1\).

For \(x=3\) the series equals the harmonic series \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}\), which is divergent.

For \(x=1\) the series equals the alternating harmonic series \(\displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}\), which is (conditionally) convergent.

We conclude that the series converges if \(x\in[1,3)\) and diverges otherwise. The interval \([1,3)\) is called the interval of convergence of the series.

Theorem: For a given power series

\[\sum_{n=0}^{\infty}c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+\cdots,\]

there are only three possibilities:

1. The series only converges for \(x=a\) (then the radius of convergence is \(R=0\)),


2. The series converges for all \(x\) (then the radius of convergence is \(R=\infty\)),


3. There is a positive number \(R\) (the radius of convergence) such that the series absolutely converges for \(|x-a| < R\) and diverges for \(|x-a| > R\).

Examples:

1) The series \(\displaystyle\sum_{n=0}^{\infty}n!(x-1)^n\) is a power series about \(1\). Hence, the series converges for \(x=1\) (with sum \(1\)). For \(x\neq1\) we apply the ratio test: let \(a_n=n!(x-1)^n\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(n+1)!(x-1)^{n+1}}{n!(x-1)^n}\right| =\lim\limits_{n\to\infty}(n+1)|x-1|=\infty,\]

since \(|x-1| > 0\). This implies that the series diverges for all \(x\neq1\). Hence, the series only converges for \(x=1\) and the radius of convergence is \(R=0\).

2) The series \(\displaystyle\sum_{n=0}^{\infty}\frac{(x+2)^n}{n!}\) is a power series about \(-2\). Hence, the series converges for \(x=-2\) (with sum \(1\)). For \(x\neq-2\) we apply the ratio test: let \(a_n=\displaystyle\frac{(x+2)^n}{n!}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(x+2)^{n+1}}{(n+1)!}\cdot\frac{n!}{(x+2)^n}\right| =\lim\limits_{n\to\infty}\frac{|x+2|}{n+1}=0.\]

This implies that the series converges for all \(x\neq-2\) as well. Hence, the series converges for all \(x\in\mathbb{R}\) and the radius of convergence is \(R=\infty\).

3) The series \(\displaystyle\sum_{n=1}^{\infty}\frac{x^{n+1}}{n^2}\) is a power series about \(0\). Hence, the series converges for \(x=0\) (with sum \(0\)). For \(x\neq0\) we apply the ratio test: let \(a_n=\displaystyle\frac{x^{n+1}}{n^2}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{x^{n+2}}{(n+1)^2}\cdot\frac{n^2}{x^{n+1}}\right| =\lim\limits_{n\to\infty}\left(\frac{n}{n+1}\right)^2|x|=|x|.\]

This implies that the series absolutely converges for \(|x| < 1\) and diverges for \(|x| > 1\). So the radius of convergence is \(R=1\). For \(x=1\) we have \(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}\) which is a \(p\)-series with \(p=2>1\) and therefore (absolutely) convergent. For \(x=-1\) we have \(\displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}\) which is absolutely convergent as well. Hence, the interval of convergence is \([-1,1]\).

4) The series \(\displaystyle\sum_{n=0}^{\infty}\frac{(3-x)^n}{n+1}\) is a power series about \(3\). Hence, the series converges for \(x=3\) (with sum \(1\)). For \(x\neq3\) we might apply the ratio test: let \(a_n=\displaystyle\frac{(3-x)^n}{n+1}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(3-x)^{n+1}}{n+2}\cdot\frac{n+1}{(3-x)^n}\right| =\lim\limits_{n\to\infty}\frac{n+1}{n+2}\cdot|3-x|=|3-x|.\]

Hence, the series is absolutely convergent if \(|3-x| < 1\) and is divergent if \(|3-x| > 1\). So the radius of convergence is \(R=1\). For \(x=2\) the series equals the harmonic series \(\displaystyle\sum_{n=0}^{\infty}\frac{1}{n+1}\), which is divergent and for \(x=4\) the series equals the alternating harmonic series \(\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^n}{n+1}\), which is (conditionally) convergent. Hence, the interval of convergence is \((2,4]\).

5) The series \(\displaystyle\sum_{n=1}^{\infty}n\left(\frac{x-5}{2}\right)^n\) is a power series about \(5\). Hence, the series converges for \(x=5\) (with sum \(0\)). For \(x\neq5\) we might apply the ratio test: let \(a_n=\displaystyle n\left(\frac{x-5}{2}\right)^n\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|(n+1)\left(\frac{x-5}{2}\right)^{n+1}\cdot\frac{1}{n}\left(\frac{2}{x-5}\right)^n\right| =\lim\limits_{n\to\infty}\frac{n+1}{n}\cdot\left|\frac{x-5}{2}\right|=\left|\frac{x-5}{2}\right|.\]

Hence, the series is absolutely convergent if \(\displaystyle\left|\frac{x-5}{2}\right| < 1\) or \(|x-5| < 2\) and is divergent if \(\displaystyle\left|\frac{x-5}{2}\right| > 1\) or \(|x-5| > 2\). So the radius of convergence is \(R=2\). For \(x=7\) the series reads \(\displaystyle\sum_{n=1}^{\infty}n\), which is divergent and for \(x=3\) the series reads \(\displaystyle\sum_{n=1}^{\infty}n(-1)^n\), which is divergent as well. Hence, the interval of convergence is \((3,7)\).

Bessel functions

Stewart §11.8, Example 3
Bessel functions are defined in terms of power series. The German astronomer Friedrich Bessel (1784-1846) introduced these functions when solving Kepler's equation for describing planetary motion. Later, these Bessel functions have been applied in many different physical situations, including the temperature distribution in a circular plate and the shape of a vibrating drumhead.\({}^{(*)}\)

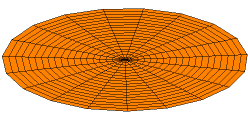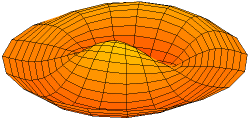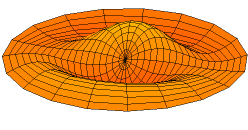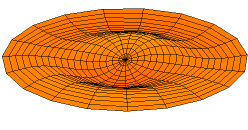
The Bessel function of the first kind of order \(0\) is defined by: \(J_0(x)=\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{2^{2n}(n!)^2}\).

Note that this is a power series in \(x\) which is convergent for \(x=0\). For \(x\neq0\) we might apply the ratio test: let \(a_n=\displaystyle\frac{(-1)^nx^{2n}}{2^{2n}(n!)^2}\), then we have:

\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim\limits_{n\to\infty}\left|\frac{(-1)^{n+1}x^{2n+2}}{2^{2n+2}((n+1)!)^2}\cdot\frac{2^{2n}(n!)^2}{(-1)^nx^{2n}}\right| =\lim\limits_{n\to\infty}\frac{x^2}{4(n+1)^2}=0.\]

Hence, the series converges for all \(x\neq0\) as well. We conclude that the power series converges for all \(x\in\mathbb{R}\) (the radius of convergence is \(R=\infty\). This implies that the domain of the Bessel function \(J_0(x)\), the interval of convergence of the series, is \((-\infty,\infty)=\mathbb{R}\).

(*) Source: https://en.wikipedia.org/wiki/Vibrations_of_a_circular_membrane.

---

Last modified on March 15, 2021