Analyse – Vectoranalyse – Vectorvelden

Definitie: Laat \(D\) een verzamling in \(\mathbb{R}^2\) zijn. Een vectorveld op \(\mathbb{R}^2\) is een functie \(\mathbf{F}\) die aan elk punt \((x,y)\) in \(D\) een tweedimensionale vector \(\mathbf{F}(x,y)\) toevoegt.

Notatie: \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}=\langle P,Q \rangle\).

De functies \(P(x,y)\) en \(Q(x,y)\) heten de componentfuncties van het vectorveld \(\mathbf{F}(x,y)\).

Stewart §16.1, Voorbeeld 1
Een vectorveld op \(\mathbb{R}^2\) wordt gedefinieerd door \(\mathbf{F}(x,y)=-y\,\mathbf{i}+x\,\mathbf{j}\). Beschrijf \(\mathbf{F}\) door enkele vectoren \(\mathbf{F}(x,y)\) te schetsen.

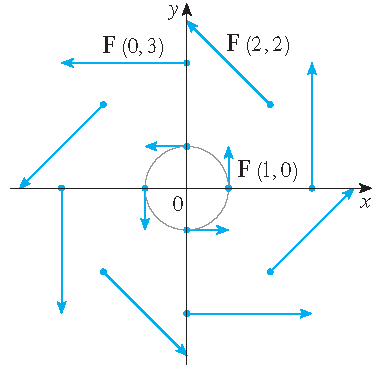
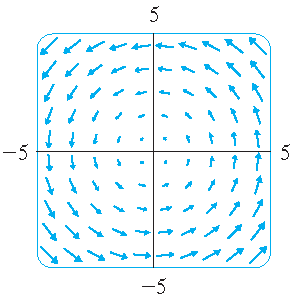
Meer voorbeelden:

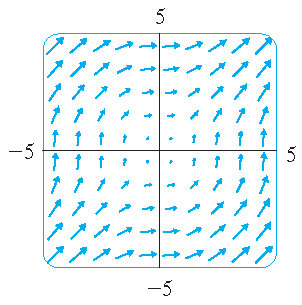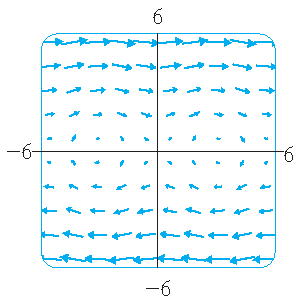
\(\mathbf{F}(x,y)=\langle -y,x \rangle\)	\(\mathbf{F}(x,y)=\langle y,\sin(x) \rangle\)	\(\mathbf{F}(x,y)=\langle \ln(1+y^2),\ln(1+x^2) \rangle\)

Definitie: Laat \(E\) een deelverzameling van \(\mathbb{R}^3\) zijn. Een vectorveld op \(\mathbb{R}^3\) is een functie \(\mathbf{F}\) die aan elk punt \((x,y,z)\) in \(E\) een driedimsionale vector \(\mathbf{F}(x,y,z)\) toevoegt.

Notatie: \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}=\langle P,Q,R \rangle\).

De functies \(P(x,y,z)\), \(Q(x,y,z)\) en \(R(x,y,z)\) heten de componentfuncties van het vectorveld \(\mathbf{F}(x,y,z)\).

Voorbeelden:

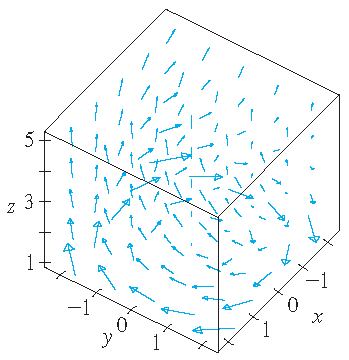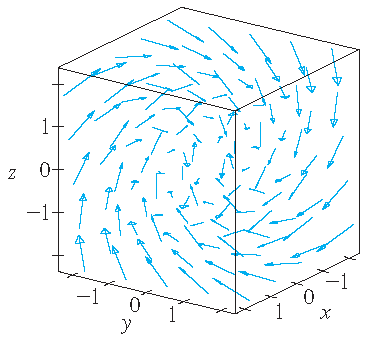
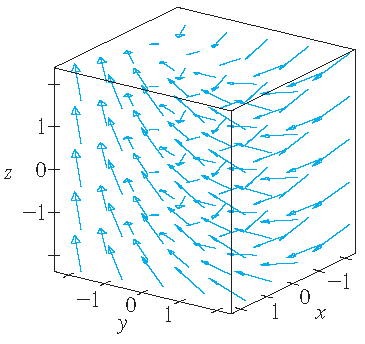
\(\mathbf{F}(x,y,z)=\langle y,z,x \rangle\)	\(\mathbf{F}(x,y,z)=\langle y,-2,x \rangle\)	\(\mathbf{F}(x,y,z)=\langle \frac{y}{z},-\frac{x}{z},\frac{z}{4} \rangle\)

Voorbeelden van een vectorveld:

• snelheidsveld (van een vloeistoef of een gas);


• zwaartekrachtveld;


• krachtveld;


• electrisch veld;


• gradiëntvectorveld.

Zie ook deze voorbeelden van vectorvelden uit het dagelijks leven.

Gradiënt(vector)veld

Definitie: Als \(f\) een scalaire functie is van twee variabelen, dan is

\[\nabla f(x,y)=f_x(x,y)\,\mathbf{i}+f_y(x,y)\,\mathbf{j}\]

een gradiënt(vector)veld op \(\mathbb{R}^2\).

Evenzo, als \(f\) een scalaire functie is van drie variabelen, dan is

\[\nabla f(x,y,z)=f_x(x,y,z)\,\mathbf{i}+f_y(x,y,z)\,\mathbf{j}+f_z(x,y,z)\,\mathbf{k}\]

een gradiënt(vector)veld op \(\mathbb{R}^3\).

Stewart §16.1, Voorbeeld 6
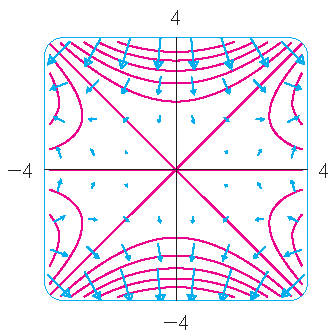
Bepaal het gradiëntvectorveld van \(f(x,y)=x^2y-y^3\). Plot het gradiëntvectorveld samen met een hoogtekaart van \(f\). Hoe zijn deze gerelateerd?

Oplossing: Het gradiëntvectorveld wordt gegeven door

\[\nabla f(x,y)=\langle f_x(x,y),f_y(x,y) \rangle=\langle 2xy,x^2-3y^2 \rangle.\]

Het plaatje toont een hoogtekaart van \(f\) met het gradiëntvectorveld. The gradiëntvectoren staan loodrecht op de niveaukrommen. Bovendien zijn de gradiëntvectoren lang waar de niveaukrommen dicht naast elkaar liggen en kort waar de krommen verder uit elkaar liggen. Dit omdat de lengte van de gradiëntvector gelijk is aan de waarde van de richtingsvector van \(f\) en dicht naast elkaar liggende niveaukrommen duiden op een steile grafiek.

Conservatieve vectorvelden

Definitie: Een vectorveld \(\mathbf{F}\) heet een conservatief vectorveld als het de gradiënt is van een zekere scalaire functie, dat wil zeggen, als er een functie \(f\) bestaat zodat \(\mathbf{F}=\nabla f\). Zo'n functie \(f\) heet een potentiaalfunctie voor \(\mathbf{F}\).

---

Laatst gewijzigd op 7 oktober 2021