OnderwijsAnalyse – Vectoranalyse – De oppervlakte van een oppervlak
Parameteroppervlakken
We beschouwen een parameteroppervlak \(S\) gegeven door:
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D.\]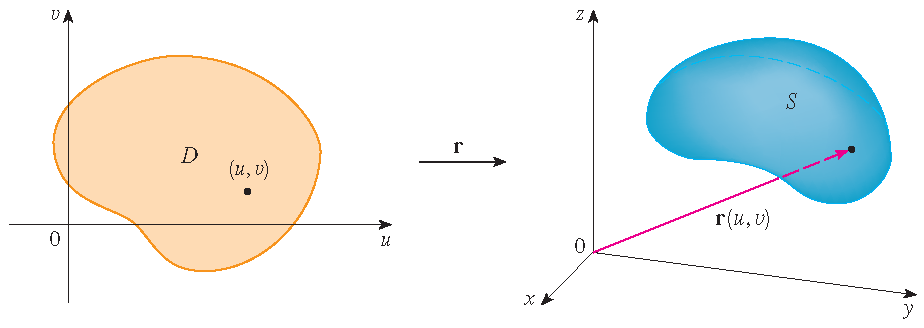
Dit heet een parametrisering van het oppervlak \(S\) met \(D\) het domein van de parametrisering.
Opmerking: Gewoonlijk nemen we aan dat \(\mathbf{r}(u,v)\) injectief is op het binnengebied van het parameterdomein \(D\).
Stewart §16.6, Voorbeeld 1
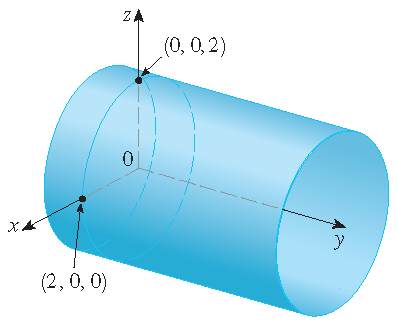
Identificeer en schets het oppervlak met parametrisering \(\mathbf{r}(u,v)=2\cos(u)\,\mathbf{i}+v\,\mathbf{j}+2\sin(u)\,\mathbf{k}\).
Oplossing: Merk op dat \(x=2\cos(u)\) en \(z=2\sin(u)\) waaruit volgt dat \(x^2+z^2=4\). Dit leidt tot een cirkelvormige cilinder met straal \(2\) waarvan de as de \(y\)-as is:
Rasterkrommen
Als een parameteroppervlak \(S\) gegeven wordt door een vectorfunctie \(\mathbf{r}(u,v)\), dan zijn er twee handige families van krommen die op \(S\) liggen, één familie met \(u\) constant en de andere met \(v\) constant. Deze families corresponderen met verticale en horiozntale lijnen in het \(uv\)-vlak.
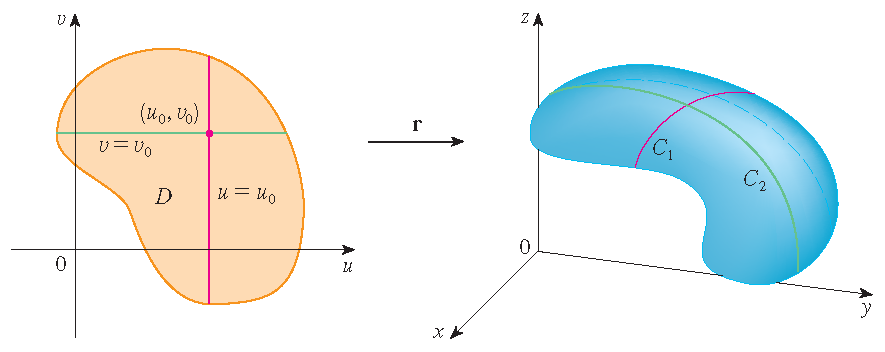
Als we \(u\) constant houden door \(u=u_0\) te stellen, dan wordt \(\mathbf{r}(u_0,v)\) een vectorfunctie met één parameter \(v\) die een kromme \(\mathcal{C}_1\) op \(S\) voorstelt. Evenzo, als we \(v\) constant houden door \(v=v_0\) te stellen, dan krijgen we een kromme \(\mathcal{C}_2\) gegeven door \(\mathbf{r}(u,v_0)\) die op \(S\) ligt. Deze krommen worden rasterkrommen genoemd.
Stewart §16.6, Voorbeeld 4
Bepaal een parametervoorstelling van de bol \(x^2+y^2+z^2=a^2\) met \(a > 0\).
Oplossing: In bolcoördinaten heeft de bol de eenvoudige representatie \(\rho=a\). We zouden daarom de hoeken \(\theta\) en \(\phi\) in bolcoördinaten kunnen gebruiken als de parameters:
\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k}, \quad 0\leq\phi\leq \pi,\quad 0\leq\theta\leq 2\pi.\]Stewart §16.6, Voorbeeld 5
Bepaal een parametervoorstelling of parametrisering voor de cilinder \(x^2+y^2=4\) en \(0\leq z\leq 1\).
Oplossing: In cilindercoördinten heeft de cilinder de eenvoudige representatie \(r=2\). Als we dan de parameters \(\theta\) en \(z\) in cilindercoördinaten kiezen, dan volgt:
\[\mathbf{r}(\theta,z)=2\cos(\theta)\,\mathbf{i}+2\sin(\theta)\,\mathbf{j}+z\,\mathbf{k},\quad 0\leq\theta\leq 2\pi,\quad 0\leq z\leq 1.\]Parametervoorstellingen of parametriseringen van oppervlakken zijn niet uniek. In de volgende twee voorbeelden zien we verschillende manieren om een oppervlak te parametriseren.
Stewart §16.6, Voorbeeld 6
Bepaal een vectorfunctie die de elliptische paraboloïde \(z=x^2+2y^2\) representeert.
Oplossing: Merk op dat het oppervlak de grafiek is van de functie \(f(x,y)=x^2+2y^2\) van twee variabelen \(x\) en \(y\). Als we dus \(x\) en \(y\) kiezen als parameters, dan volgt
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x^2+2y^2)\,\mathbf{k}.\]Een andere parametrisering zou kunnen zijn:
\[\mathbf{r}(r,\theta)=\sqrt{2}\,r\cos(\theta)\,\mathbf{i}+r\sin(\theta)\,\mathbf{j}+2r^2\,\mathbf{k},\quad r\geq0,\quad 0\leq\theta\leq 2\pi.\]Stewart §16.6, Voorbeeld 7
Bepaal een parametervoorstelling voor het oppervlak \(z=2\sqrt{x^2+y^2}\), dat wil zeggen, de bovenste helft van de kegel \(z^2=4x^2+4y^2\).
Oplossing: Weer kan het oppervlak worden gezien als de grafiek van een functie van twee variabelen:
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+2\sqrt{x^2+y^2}\,\mathbf{k}.\]Een andere parametrisering is gebaseerd op de poolcoördinaten \(r\) en \(\theta\):
\[\mathbf{r}(r,\theta)=r\cos(\theta)\,\mathbf{i}+r\sin(\theta)\,\mathbf{j}+2r\,\mathbf{k},\quad r\geq0,\quad 0\leq\theta\leq 2\pi.\]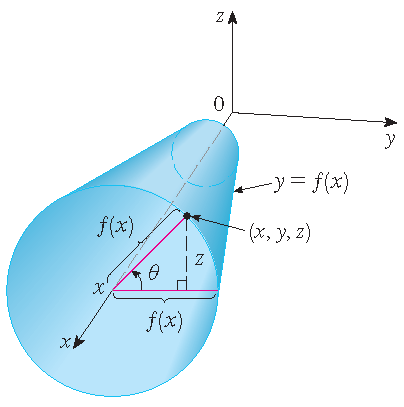
Omwentelingsoppervlakken
Beschouw het oppervlak \(S\) dat wordt verkregen door de kromme \(y=f(x)\) met \(a\leq x\leq b\) te wentelen rond de \(x\)-as, waarbij \(f(x)\geq 0\). Laat \(\theta\) de omwentelingshoek zijn, dan geldt
\[S:\;\mathbf{r}(x,\theta)=x\,\mathbf{i}+f(x)\cos(\theta)\,\mathbf{j}+f(x)\sin(\theta)\,\mathbf{k},\quad a\leq x\leq b,\quad 0\leq\theta\leq2\pi.\]Zie het plaatje rechts.
Stewart §16.6, Voorbeeld 8
Bepaal een parametrisering van het oppervlak dat ontstaat door de kromme \(y=\sin(x)\) met \(0\leq x\leq 2\pi\) te wentelen rond de \(x\)-as.
Oplossing: Er geldt
\[\mathbf{r}(x,\theta)=x\,\mathbf{i}+\sin(x)\cos(\theta)\,\mathbf{j}+\sin(x)\sin(\theta)\,\mathbf{k},\quad 0\leq x\leq 2\pi,\quad 0\leq\theta\leq 2\pi.\]Het omwentelingsoppervlak ziet er zo uit:
Raakvlakken
We willen het raakvlak bepalen aan een parameteroppervlak \(S\) beschreven door een vectorfunctie
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k}\]in een punt \(P_0\) met plaatsvector \(\mathbf{r}(u_0,v_0)\). Als we \(u\) constant houden door \(u=u_0\) te stellen, dan wordt \(\mathbf{r}(u_0,v)\) een vectorfunctie van één variabele \(v\) die een rasterkromme \(\mathcal{C}_1\) op \(S\) beschrijft. De raakvector aan \(\mathcal{C}_1\) in \(P_0\) wordt verkregen door de partiële afgeleide naar \(v\) te nemen van \(\mathbf{r}\):
\[\mathbf{r}_v=x_v(u_0,v_0)\,\mathbf{i}+y_v(u_0,v_0)\,\mathbf{j}+z_v(u_0,v_0)\,\mathbf{k}.\]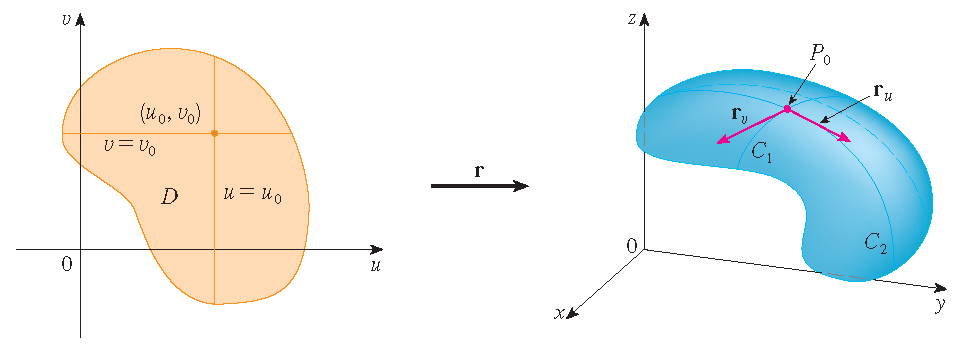
Evenzo, als we \(v\) constant houden door \(v=v_0\) te stellen, dan krijgen we een rasterkromme \(\mathcal{C}_2\) gegeven door \(\mathbf{r}(u,v_0)\) die op \(S\) ligt en de raakvector in \(P_0\) is dan
\[\mathbf{r}_u=x_u(u_0,v_0)\,\mathbf{i}+y_u(u_0,v_0)\,\mathbf{j}+z_u(u_0,v_0)\,\mathbf{k}.\]Als \(\mathbf{r}_u\times\mathbf{r}_v\) niet gelijk is aan \(\mathbf{0}\), dan heet het oppervlak \(S\) glad. Voor een glad oppervlak is het raakvlak het vlak dat de raakvectoren \(\mathbf{r}_u\) en \(\mathbf{r}_v\) bevat en de vector \(\mathbf{r}_u\times\mathbf{r}_v\) is een normaalvector van het raakvlak.
De oppervlakte van een oppervlak
We willen de oppervlakte bepalen van een parameteroppervlak. We beginnen met een oppervlak waarvan het parameterdomein \(D\) een rechthoek is en verdelen dit in deelrechthoeken \(R_{ij}\). We kiezen \((u_i^*,v_j^*)\) als het linker onderste hoekpunt van \(R_{ij}\):
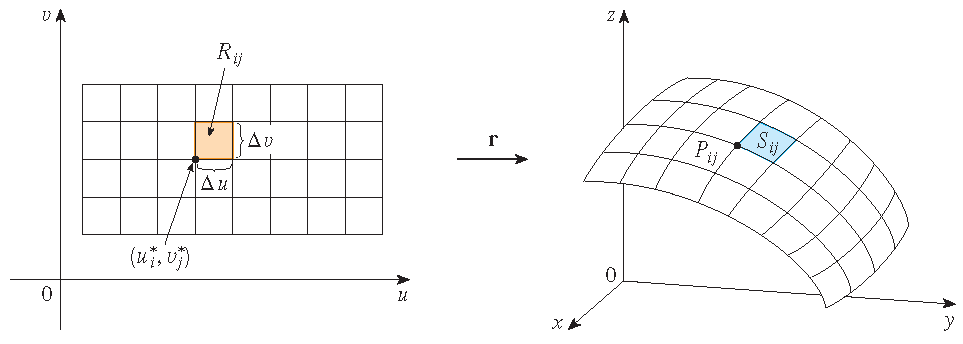
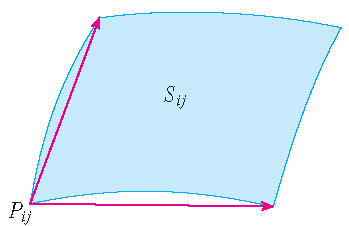
Het deel \(S_{ij}\) van het oppervlak \(S\) dat correspondeert met \(R_{ij}\) heet een patch en heeft het punt \(P_{ij}\) met plaatsvector \(\mathbf{r}(u_i^*,v_j^*)\) als één van de hoekpunten. Laat
\[\mathbf{r}_u^*=\mathbf{r}_u(u_i^*,v_j^*)\quad\textrm{en}\quad\mathbf{r}_v^*=\mathbf{r}_v(u_i^*,v_j^*)\]de raakvectoren zijn in \(P_{ij}\).
 |
 |
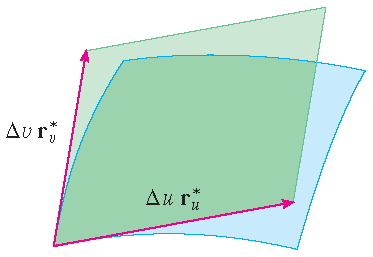Het plaatje laat zien dat de twee randen van de patch die in \(P_{ij}\) bij elkaar komen kunnen worden benaderd door vectoren. Deze vectoren, op hun beurt, kunnen worden benaderd door de vectoren \(\Delta u\,\mathbf{R}_u^*\) en \(\Delta v\,\mathbf{r}_v^*\) omdat partiële afgeleiden kunnen worden benaderd door differentiequotiënten. We benaderen zo dus \(S_{ij}\) door het parallellogram opgespannen door de vectoren \(\Delta u\,\mathbf{r}_u^*\) en \(\Delta v\,\mathbf{r}_v^*\). Dit parallellogram wordt getoond in het plaatje en ligt in het raakvlak aan \(S\) in \(P_{ij}\). De oppervlakte van dit parallellogram is
\[\left|\left(\Delta u\,\mathbf{r}_u^*\right)\times\left(\Delta v\,\mathbf{r}_v^*\right)\right| =\left|\mathbf{r}_u^*\times\mathbf{r}_v^*\right|\,\Delta u\,\Delta v.\]Een benadering van de oppervlakte van \(S\) is dus
\[\sum_{i=1}^m\sum_{j=1}^n\left|\mathbf{r}_u^*\times\mathbf{r}_v^*\right|\,\Delta u\,\Delta v.\]Deze benadering wordt steeds beter als we het aantal deelrechthoeken laten toenemen en we herkennen de dubbele som als een Riemannsom voor een tweevoudige integraal. Dit motiveert de volgende definitie.
Definitie: Als een glad oppervlak \(S\) wordt gegeven door
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D\]en \(S\) wordt precies één keer doorlopen als \((u,v)\) door het parameterdomein \(D\) loopt, dan is de oppervlakte van het oppervlak \(S\) gelijk aan
\[\textrm{opp}(S)=\iint\limits_D\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA,\]waarbij \(\displaystyle\mathbf{r}_u=\frac{\partial x}{\partial u}\,\mathbf{i}+\frac{\partial y}{\partial u}\,\mathbf{j}+\frac{\partial z}{\partial u}\,\mathbf{k}\) en \(\displaystyle\mathbf{r}_v=\frac{\partial x}{\partial v}\,\mathbf{i}+\frac{\partial y}{\partial v}\,\mathbf{j}+\frac{\partial z}{\partial v}\,\mathbf{k}\).
Stewart §16.6, Voorbeeld 10
Bepaal de oppervlakte van een boloppervlak met straal \(a > 0\).
Oplossing: Een parametrisering van de bol is
\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq \pi,\quad 0\leq\theta\leq 2\pi.\]Het uitwendig product van de raakvectoren
\[\mathbf{r}_{\phi}=a\,\cos(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\cos(\phi)\,\sin(\theta)\,\mathbf{j}-a\,\sin(\phi)\,\mathbf{k}\quad\textrm{en}\quad \mathbf{r}_{\theta}=-a\,\sin(\phi)\,\sin(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\cos(\theta)\,\mathbf{j}+0\,\mathbf{k}\]is
\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=a^2\,\sin^2(\phi)\,\cos(\theta)\,\mathbf{i}+a^2\,\sin^2(\phi)\,\sin(\theta)\,\mathbf{j} +a^2\,\sin(\phi)\,\cos(\phi)\,\mathbf{k}=a\,\sin(\phi)\cdot\mathbf{r}(\phi,\theta).\]Dus geldt
\[\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|=a\,|\sin(\phi)|\cdot a=a^2\,\sin(\phi),\]since \(\sin(\phi)\geq0\) for \(0\leq\phi\leq\pi\). Therefore, using the definition, the area of the sphere is
\[\iint\limits_D\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA=\int_0^{2\pi}\int_0^{\pi}a^2\,\sin(\phi)\,d\phi\,d\theta =a^2\int_0^{2\pi}\,d\theta\,\int_0^{\pi}\sin(\phi)\,d\phi=a^2\cdot2\pi\cdot2=4]pi a^2.\]Stewart §16.6, Voorbeeld 11
Bepaal de oppervlakte van het deel van de paraboloïde \(z=x^2+y^2\) dat onder het vlak \(z=9\) ligt.
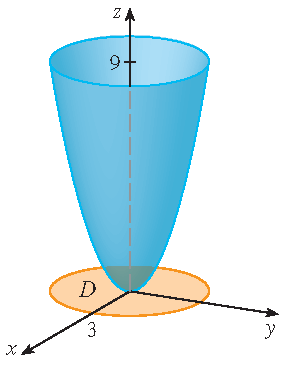
Oplossing: Het vlak \(z=9\) snijdt de paraboloïde in de cirkel \(x^2+y^2=9\). Het gegeven oppervlak ligt dus boven de cirkelschijf \(D\) met middelpunt de oorsprong en straal \(3\). Een parametrisering van het oppervlak is
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x^2+y^2)\,\mathbf{k},\quad (x,y)\in D=\{(x,y)\,|\,x^2+y^2\leq 9\}.\]De oppervlakte van het oppervlak is dus gelijk aan \(\displaystyle\iint\limits_D\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA\) met \(\mathbf{r}_x=\mathbf{i}+2x\,\mathbf{k}\) en \(\mathbf{r}_y=\mathbf{j}+2y\,\mathbf{k}\). Nu geldt
\[\left|\mathbf{r}_x\times\mathbf{r}_y\right|=\left|-2x\,\mathbf{i}-2y\,\mathbf{j}+\mathbf{k}\right|=\sqrt{(-2x)^2+(-2y)^2+1} =\sqrt{4x^2+4y^2+1}.\]Met behulp van poolcoördinaten volgt dat de oppervlakte van het oppervlak gelijk is aan
\begin{align*} \iint\limits_D\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA&=\iint\limits_D\sqrt{4x^2+4y^2+1}\,dA =\int_0^{2\pi}\int_0^3\sqrt{4r^2+1}\,r\,dr\,d\theta=\int_0^{2\pi}\,d\theta\,\int_0^3r\sqrt{4r^2+1}\,dr\\[2.5mm] &=2\pi\bigg[\frac{1}{12}(4r^2+1)^{3/2}\bigg]_{r=0}^3=\frac{1}{6}\pi\left(37\sqrt{37}-1\right). \end{align*}De oppervlakte van een torus
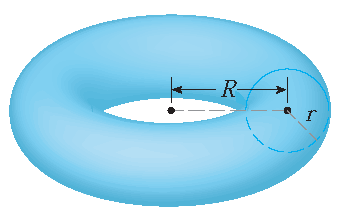Een parametrisering van een torus die wordt verkregen door een verticale cirkel met straal \(r\) te wentelen om de \(z\)-as, waarbij het
middelpunt van de cirkel zich op een afstand \(R\) van de \(z\)-as met \(0 < r < R\) bevindt, is
met \(0\leq\theta\leq2\pi\) en \(0\leq\phi\leq2\pi\).
Merk op dat het volume gelijk is aan \(2\pi\,R\cdot\pi\,r^2=2\pi^2\,r^2\,R\), het product van de omtrek van een cirkel met straal \(R\) en de oppervlakte van een cirkel met straal \(r\).
Om de oppervlakte van de torus te berekenen volgt
\begin{align*} \mathbf{r}_{\theta}\times\mathbf{r}_{\phi}&=\langle-(R+r\,\cos(\phi))\sin(\theta),(R+r\,\cos(\phi)\cos(\theta),0\rangle\times \langle -r\,\sin(\phi)\,\cos(\theta),-r\,\sin(\phi)\,\sin(\theta),r\,\cos(\phi)\rangle\\[2.5mm] &=\langle r\,\cos(\phi)(R+r\,\cos(\phi))\cos(\theta),r\,\cos(\phi)(R+r\,\cos(\phi))\sin(\theta), r\,\sin(\phi)(R+r\,\cos(\phi))(\cos^2(\theta)+\sin^2(\theta))\rangle\\[2.5mm] &=\langle r\,\cos(\phi)(R+r\,\cos(\phi))\cos(\theta),r\,\cos(\phi)(R+r\,\cos(\phi))\sin(\theta), r\,\sin(\phi)(R+r\,\cos(\phi))\rangle\\[2.5mm] &=r\,(R+r\,\cos(\phi))\langle \cos(\phi)\,\cos(\theta),\cos(\phi)\,\sin(\theta),\sin(\phi)\rangle \end{align*}en dus
\[\left|\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}\right|=r\,(R+r\,\cos(\phi))\sqrt{\cos^2(\phi)\left(\cos^2(\theta)+\sin^2(\theta)\right)+\sin^2(\phi)} =r\,(R+r\,\cos(\phi))\sqrt{\cos^2(\phi)+\sin^2(\phi)}=r\,(R+r\,\cos(\phi)).\]De oppervlakte van de torus is dus
\begin{align*} \int_0^{2\pi}\int_0^{2\pi}\left|\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}\right|\,d\phi\,d\theta &=\int_0^{2\pi}\int_0^{2\pi}r\,(R+r\,\cos(\phi))\,d\phi\,d\theta=2\pi\,r\,\int_0^{2\pi}(R+r\,\cos(\phi))\,d\phi =2\pi\,r\,\bigg[R\phi+r\,\sin(\phi)\bigg]_{\phi=0}^{2\pi}\\[2.5mm] &=2\pi\,r\cdot2\pi\,R=4\pi^2\,r\,R, \end{align*}het product van de omtrek van een cirkel met straal \(r\) en de omtrek van een cirkel met straal \(R\).
Laatst gewijzigd op 16 oktober 2021
