Analyse – Vectoranalyse – De stelling van Green

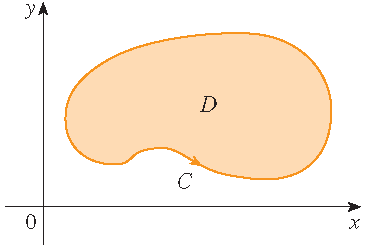
Definitie: Voor een enkelvoudig gesloten kromme \(\mathcal{C}\) refereert de positieve oriëntatie aan een enkele rondgang tegen de wijzers van de klok in van \(\mathcal{C}\).

positieve oriëntatie	negatieve oriëntatie

Definitie: Een gebied \(D\) in \(\mathbb{R}^2\) heet een regulier gebied als het zowel van type I als van type II is.

Stelling: Laat \(\mathcal{C}\) een positief georiënteerde, stuksgewijs gladde, enkelvoudig gesloten in het vlak zijn en laat \(D\) het gebied zijn dat begrensd wordt door \(\mathcal{C}\). Als \(P\) en \(Q\) continue partiële afgeleiden hebben op een open gebied dat \(D\) bevat, dan is

\[\oint\limits_{\mathcal{C}}P\,dx+Q\,dy=\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA.\]

Opmerking: Soms wordt de notatie \(\partial D\) gebruikt voor de postief georiënteerde randkromme van \(D\), dat wil zeggen: \(\mathcal{C}=\partial D\). Dan is

\[\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA=\oint\limits_{\partial D}P\,dx+Q\,dy.\]

Bewijs (alleen voor reguliere gebieden die zowel van type I als van type II zijn): Merk op dat de stelling is bewezen als we kunnen aantonen dat

\[\oint\limits_{\mathcal{C}}P\,dx=-\iint\limits_D\frac{\partial P}{\partial y}\,dA\quad\textrm{en}\quad \oint\limits_{\mathcal{C}}Q\,dy=\iint\limits_D\frac{\partial Q}{\partial x}\,dA.\]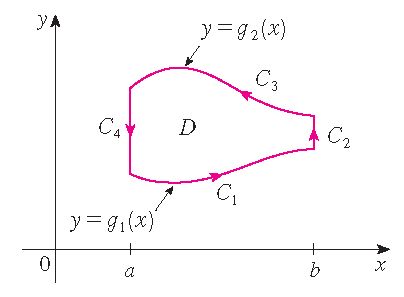

Omdat \(D\) een type I gebied is, geldt: \(D=\{(x,y)\,|\,a\leq x\leq b,\;g_1(x)\leq y\leq g_2(x)\}\), waarbij \(g_1\) en \(g_2\) continue functies zijn. Hiermee kunnen de tweevoudige integraal \(\displaystyle\iint\limits_D\frac{\partial P}{\partial y}\,dA\) berekenen:

\[\iint\limits_D\frac{\partial P}{\partial y}\,dA=\int_a^b\int_{g_1(x)}^{g_2(x)}\frac{\partial P}{\partial y}\,dy\,dx =\int_a^b\left(P(x,g_2(x))-P(x,g_1(x)\right)\,dx.\]

Nu berekenen we de lijnintegraal \(\displaystyle\oint\limits_{\mathcal{C}}P\,dx\) door de kromme \(\mathcal{C}\) op te delen in een vereniging van vier krommen \(\mathcal{C}_1\), \(\mathcal{C}_2\), \(\mathcal{C}_3\) en \(\mathcal{C}_4\) zoals in het plaatje.

Op \(\mathcal{C}_2\) en \(\mathcal{C}_4\) is \(x\) constant, dus \(dx=0\), en dus \(\displaystyle\int\limits_{\mathcal{C}_2}P(x,y)\,dx=0=\int\limits_{\mathcal{C}_4}P(x,y)\,dx\).

Een parametrisering van \(\mathcal{C}_1\) is \(\mathbf{r}(x)=x\,\mathbf{i}+g_1(x)\,\mathbf{j}\) met \(a\leq x\leq b\). Dan volgt: \(\displaystyle\int\limits_{\mathcal{C}_1}P(x,y)\,dx=\int_a^bP(t,g_1(t))\,dt\). Merk verder op dat een parametrisering van \(-\mathcal{C}_3\) is \(\mathbf{r}(x)=x\,\mathbf{i}+g_2(x)\,\mathbf{j}\) met \(a\leq x\leq b\) en dus \(\displaystyle\int\limits_{\mathcal{C}_3}P(x,y)\,dx=-\int\limits_{-\mathcal{C}_3}P(x,y)\,dx=-\int_a^bP(x,g_2(x))\,dx\). Dan volgt:

\begin{align*} \oint\limits_{\mathcal{C}}P(x,y)\,dx&=\int\limits_{\mathcal{C}_1}P(x,y)\,dx+\int\limits_{\mathcal{C}_2}P(x,y)\,dx +\int\limits_{\mathcal{C}_3}P(x,y)\,dx+\int\limits_{\mathcal{C}_4}P(x,y)\,dx\\[2.5mm] &=\int_a^bP(x,g_1(x))\,dx+0-\int_a^bP(x,g_2(x))\,dx+0=\int_a^b\left(P(x,g_2(x))-P(x,g_1(x))\right)\,dx. \end{align*}

Hieruit volgt dat \(\displaystyle\oint\limits_{\mathcal{C}}P\,dx=-\iint\limits_D\frac{\partial P}{\partial y}\,dA\). Om aan te tonen dat \(\displaystyle\oint\limits_{\mathcal{C}}Q\,dy=\iint\limits_D\frac{\partial Q}{\partial x}\,dA\) gebruiken we dat \(D\) ook een type II gebied is, waaruit volgt dat \(D=\{(x,y)\,|\,c\leq y\leq d,\;h_1(y)\leq x\leq h_2(y)\}\), waarbij \(h_1\) en \(h_2\) continue functies zijn. Dan volgt:

\[\iint\limits_D\frac{\partial Q}{\partial x}\,dA=\int_c^d\int_{h_1(y)}^{h_2(y)}\frac{\partial Q}{\partial x}\,dx\,dy =\int_c^d\left(Q(h_2(y),y)-Q(h_1(y),y\right)\,dy.\]

Evenzo berekenen we de lijnintegraal \(\displaystyle\oint\limits_{\mathcal{C}}Q\,dy\) door de kromme \(\mathcal{C}\) op te delen in een vereniging van vier krommen \(\mathcal{C}_1\), \(\mathcal{C}_2\), \(\mathcal{C}_3\) en \(\mathcal{C}_4\), waarbij \(y\) constant is op zowel \(\mathcal{C}_1\) als \(\mathcal{C}_3\) en dus \(\displaystyle\int\limits_{\mathcal{C}_1}Q(x,y)\,dy=0=\int\limits_{\mathcal{C}_3}Q(x,y)\,dy\).

Een parametrisering van \(\mathcal{C}_2\) is \(\mathbf{r}(y)=h_2(y)\,\mathbf{i}+y\,\mathbf{j}\) met \(c\leq y\leq d\) en een parametrisering van \(-\mathcal{C}_4\) is \(\mathbf{r}(y)=h_1(y)\,\mathbf{i}+y\,\mathbf{j}\) met \(c\leq y\leq d\) en dus \begin{align*} \oint\limits_{\mathcal{C}}Q(x,y)\,dy&=\int\limits_{\mathcal{C}_1}Q(x,y)\,dy+\int\limits_{\mathcal{C}_2}Q(x,y)\,dy +\int\limits_{\mathcal{C}_3}Q(x,y)\,dy+\int\limits_{\mathcal{C}_4}Q(x,y)\,dy\\[2.5mm] &=0+\int_c^dQ(h_2(y),y)\,dy+0-\int_c^dQ(h_1(y),y)\,dy=\int_c^d\left(Q(h_2(y),y)-Q(h_1(y),y)\right)\,dy. \end{align*}

Hieruit volgt dat \(\displaystyle\oint\limits_{\mathcal{C}}Q\,dy=\iint\limits_D\frac{\partial Q}{\partial x}\,dA\).

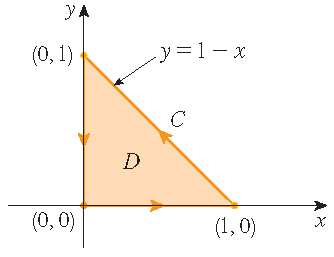Stewart §16.4, Voorbeeld 1
Bereken \(\displaystyle\int\limits_{\mathcal{C}}x^4\,dx+xy\,dy\), waarbij \(\mathcal{C}\) de driehoekige kromme is bestaande uit de lijnstukken van \((0,0)\) tot \((1,0)\), van \((1,0)\) tot \((0,1)\) en van \((0,1)\) tot \((0,0)\) met positieve oriëntatie.

Oplossing: De lijnintegraal kan rechtstreeks worden berekend met behulp van parametriseringen van de drie delen van de kromme \(\mathcal{C}\). Het lijnstuk van \((0,0)\) tot \((1,0)\) kan worden geparametriseerd door \(\mathbf{r}(t)=\langle t,0 \rangle\) met \(0\leq t\leq 1\), het lijnstuk van \((1,0)\) tot \((0,1)\) door \(\mathbf{r}(t)=\langle 1-t,t \rangle\) met \(0\leq t\leq 1\) en het lijnstuk van \((0,1)\) tot \((0,0)\) door \(\mathbf{r}(t)=\langle 0,1-t \rangle\) met \(0\leq t\leq 1\). Dit leidt tot

\[\int\limits_{\mathcal{C}}x^4\,dx+xy\,dy=\int_0^1\left(t^4-(1-t)^4+t(1-t)+0\right)\,dt =\bigg[\frac{1}{5}t^5+\frac{1}{5}(1-t)^5+\frac{1}{2}t^2-\frac{1}{3}t^3\bigg]_{t=0}^1 =\frac{1}{5}+\frac{1}{2}-\frac{1}{3}-\frac{1}{5}=\frac{1}{6}.\]

Als \(P(x,y)=x^4\) en \(Q(x,y)=xy\), dan volgt uit de stelling van Green dat

\[\int\limits_{\mathcal{C}}x^4\,dx+xy\,dy=\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA =\int_0^1\int_0^{1-x}y\,dy\,dx=\int_0^1\bigg[\frac{1}{2}y^2\bigg]_{y=0}^{1-x}\,dx =\frac{1}{2}\int_0^1(1-x)^2\,dx=-\frac{1}{6}(1-x)^3\bigg|_{x=0}^1=\frac{1}{6}.\]

Stewart §16.4, Voorbeeld 2
Bereken \(\displaystyle\oint\limits_{\mathcal{C}}\left(3y-e^{\sin(x)}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy\), waarbij \(\mathcal{C}\) de cirkel \(x^2+y^2=9\) is met positieve oriëntatie.

Oplossing: Het gebied \(D\) ingesloten door de kromme \(\mathcal{C}\) is de cirkelschijf \(x^2+y^2\leq 9\). Met behulp van de stelling van Green volgt dan

\begin{align*} \oint\limits_{\mathcal{C}}\left(3y-e^{\sin(x)}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy &=\iint\limits_D\left(\frac{\partial}{\partial x}\left(7x+\sqrt{y^4+1}\right)-\frac{\partial}{\partial y}\left(3y-e^{\sin(x)}\right)\right)\,dA\\[2.5mm] &=\iint\limits_D\left(7-3\right)\,dA=4\cdot\text{area}(D)=4\cdot9\pi=36\pi. \end{align*}

Berekening van oppervlaktes

Omdat de oppervlakte van een gebied \(D\) gelijk is aan \(\displaystyle\iint\limits_D1\,dA\), kunnen we stelling van Green toepassen als \(\displaystyle\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1\) en de oppervlakte berekenen met behulp van een lijnintegraal over de postief georiënteerde randkromme \(\mathcal{C}\) die \(D\) omsluit. Er geldt bijvoorbeeld:

\[\text{opp}(D)=\oint\limits_{\mathcal{C}}x\,dy=-\oint\limits_{\mathcal{C}}y\,dx=\tfrac{1}{2}\oint\limits_{\mathcal{C}}x\,dy-y\,dx.\]

Stewart §16.4, Voorbeeld 3
Bepaal de oppervlakte van het gebied \(D\) ingesloten door de ellips \(\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) met \(a>0\) en \(b>0\).

Oplossing: Een parametrisering van de randkromme \(\mathcal{C}\) is \(\mathbf{r}(t)=a\,\cos(t)\,\mathbf{i}+b\,\sin(t)\,\mathbf{j}\) met \(0\leq t\leq 2\pi\). Dus geldt bijvoorbeel dat

\[\text{opp}(D)=\oint\limits_{\mathcal{C}}x\,dy=\int_0^{2\pi}a\,\cos(t)\,d\,b\,\sin(t)=ab\int_0^{2\pi}\cos^2(t)\,dt =\frac{1}{2}ab\int_0^{2\pi}\left(1+\cos(2t)\right)\,dt=\frac{1}{2}ab\bigg[t+\frac{1}{2}\sin(2t)\bigg]_{t=0}^{\pi}=ab\pi.\]

Evenzo geldt dat:

\[\text{opp}(D)=-\oint\limits_{\mathcal{C}}y\,dx=-\int_0^{2\pi}b\,\sin(t)\,d\,a\,\cos(t)=ab\int_0^{2\pi}\sin^2(t)\,dt =\frac{1}{2}ab\int_0^{2\pi}\left(1-\cos(2t)\right)\,dt=\frac{1}{2}ab\bigg[t-\frac{1}{2}\sin(2t)\bigg]_{t=0}^{\pi}=ab\pi.\]

Het is wellicht nog eenvoudiger als we de derde fomule gebruiken:

\[\text{opp}(D)=\tfrac{1}{2}\oint\limits_{\mathcal{C}}x\,dy-y\,dx=\tfrac{1}{2}\int_0^{2\pi}\left(a\,\cos(t)\,d\,b\,\sin(t)-b\,\sin(t)\,d\,a\,\cos(t)\right) =\tfrac{1}{2}ab\int_0^{2\pi}\left(\cos^2(t)+\sin^2(t)\right)\,dt=ab\pi.\]

Meer algemene gebieden

We hebben de stelling van Green bewezen voor reguliere gebieden \(D\) die zowel van type I als van type II zijn. Het geldt echter ook voor meer algemene gebieden die geschreven kunnen worden als een eindige vereniging van reguliere gebieden:

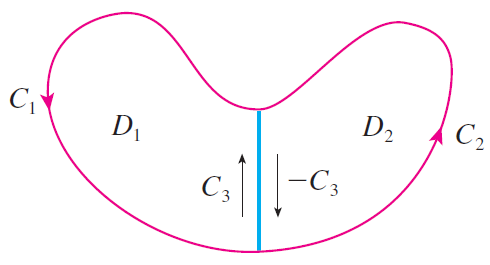Merk op dat de lijnintegralen over de blauwe lijnstukken in tegengestelde richtingen tegen elkaar wegvallen.

Stewart §16.4, Voorbeeld 4
Bereken \(\displaystyle\oint\limits_{\mathcal{C}}y^2\,dx+3xy\,dy\), waarbij \(\mathcal{C}\) de rand is van het halfringvormige gebied \(D\) in het bovenhalfvlak tussen de cirkels \(x^2+y^2=1\) en \(x^2+y^2=4\).

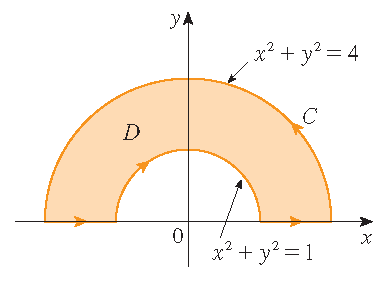
Oplossing: Merk op dat \(D\) van type I is, maar niet van type II. Echter, de \(y\)-as verdeelt het gebied \(D\) in twee delen die beide regulier zijn. Hieruit volgt dat de stelling van Green kan worden toegepast. Met behulp van poolcoördinaten volgt

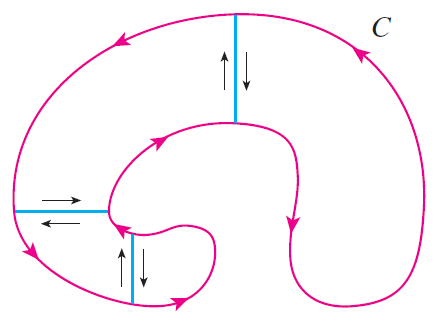
\begin{align*} \oint\limits_{\mathcal{C}}y^2\,dx+3xy\,dy&=\iint\limits_D\left(\frac{\partial}{\partial x}(3xy)-\frac{\partial}{\partial y}(y^2)\right)\,dA =\iint\limits_Dy\,dA=\int_0^{\pi}\int_1^2r\sin(\theta)\,r\,dr\,d\theta\\[2.5mm] &=\int_0^{\pi}\sin(\theta)\,d\theta\int_1^2r^2\,dr=\bigg[-\cos(\theta)\bigg]_{\theta=0}^{\pi}\cdot\bigg[\frac{1}{3}r^3\bigg]_{r=1}^2 =2\cdot\frac{7}{3}=\frac{14}{3}. \end{align*}

De stelling van Green kan worden uitgebreid naar gebieden met gaten, dat wil zeggen, gebieden die niet enkelvoudig samenhangend zijn. Merk op dat de rand \(\mathcal{C}\) van het gebied \(D\) in het plaatje bestaat uit twee enkelvoudig gesloten krommen \(\mathcal{C}_1\) en \(\mathcal{C}_2\). We nemen aan dat deze randkrommen beide zo georiënteerd zijn dat het gebied \(D\) steeds aan de linkerkant ligt als de kromme \(\mathcal{C}\) wordt doorlopen. Dan is de positieve richting van de buitenste kromme \(\mathcal{C}_1\) tegen de wijzers van de klok in en die van de binnenste kromme \(\mathcal{C}_2\) met de wijzers van de klok mee.

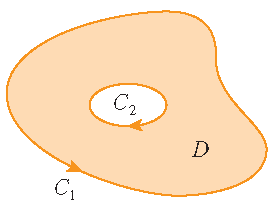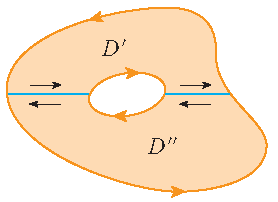Weer kunnen we het gebied \(D\) verdelen in twee gebieden \(D'\) en \(D''\) zoals in het plaatje, waarbij de lijnintegralen over de blauwe lijnstukken in tegengestelde richtingen tegen elkaar wegvallen als we de stelling van Green toepassen op beide gebieden \(D'\) en \(D''\).

Stewart §16.4, Voorbeeld 5
Als \(\mathbf{F}(x,y)=-\displaystyle\frac{y}{x^2+y^2}\,\mathbf{i}+\frac{x}{x^2+y^2}\,\mathbf{j}\), toon dan aan dat \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=2\pi\) voor elke postief georiënteerde enkelvoudig gesloten kromme \(\mathcal{C}\) die de oorsprong omsluit.

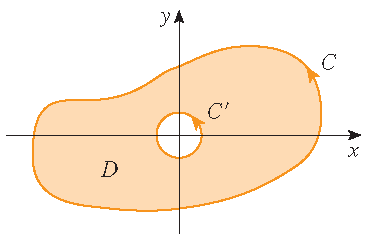
Oplossing: Omdat \(\mathcal{C}\) een willekeurige gesloten kromme is die de oorsprong omsluit, is het onmogelijk om de lijnintegraal rechtstreeks te berekenen. Echter, we kunnen een cirkel \(\mathcal{C}'\) kiezen met middelpunt de oorsprong en straal \(\delta\), waarbij \(\delta > 0\) voldoende klein is dat \(\mathcal{C}'\) binnen \(\mathcal{C}\) ligt, die tegen de wijzers van de klok in wordt doorlopen. Laat \(D\) het gebied zijn begrensd door \(\mathcal{C}\) en \(\mathcal{C}'\). Dan is de positief georiënteerde rand van \(D\) gelijk aan \(\mathcal{C}\cup\left(-\mathcal{C}'\right)\) en volgt uit de algemene versie van de stelling van Green dat

\[\oint\limits_{\mathcal{C}}P\,dx+Q\,dy+\oint\limits_{-\mathcal{C}'}P\,dx+Q\,dy =\iint\limits_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA =\iint\limits_D\left(\frac{y^2-x^2}{(x^2+y^2)^2}-\frac{y^2-x^2}{(x^2+y^2)^2}\right)\,dA=0.\]

Merk op dat \(D\) de oorsprong niet bevat. Dus geldt

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\oint\limits_{\mathcal{C}}P\,dx+Q\,dy=-\oint\limits_{-\mathcal{C}'}P\,dx+Q\,dy =\oint\limits_{\mathcal{C}'}P\,dx+Q\,dy=\oint\limits_{\mathcal{C}'}\mathbf{F}\cdot d\mathbf{r}.\]

De laatste lijnintegraal kan worden berekend met behulp van een parametrisering van \(\mathcal{C}'\) en dat is \(\mathbf{r}(t)=\delta\,\cos(t)\,\mathbf{i}+\delta\,\sin(t)\,\mathbf{j}\) met \(0\leq t\leq 2\pi\). Dan volgt

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\oint\limits_{\mathcal{C}'}\mathbf{F}\cdot d\mathbf{r} =\int_0^{2\pi}\langle -\frac{\delta\,\sin(t)}{\delta^2},\frac{\delta\,\cos(t)}{\delta^2} \rangle \cdot \langle -\delta\,\sin(t),\delta\,\cos(t) \rangle\,dt =\int_0^{2\pi}\left(\sin^2(t)+\cos^2(t)\right)\,dt=\int_0^{2\pi}dt=2\pi.\]

---

Laatst gewijzigd op 13 oktober 2021