Analyse – Vectoranalyse – De booglengte van een kromme

Parametriseringen van een kromme

Een (vlakke) kromme \(\mathcal{C}\) in \(\mathbb{R}^2\) is de verzameling van punten \((x,y)\), waarbij

\[x=f(t)\quad\textrm{en}\quad y=g(t)\quad\textrm{met}\quad a\leq t\leq b.\]

De vectorfunctie \(\mathbf{r}(t)=f(t)\,\mathbf{i}+g(t)\,\mathbf{j}\) met \(a\leq t\leq b\) heet een parametrisering van de kromme \(\mathcal{C}\).

Een (ruimte)kromme \(\mathcal{C}\) in \(\mathbb{R}^3\) is de verzameling van punten \((x,y,z)\), waarbij

\[x=f(t),\quad y=g(t)\quad\textrm{en}\quad z=h(t)\quad\textrm{met}\quad a\leq t\leq b.\]

De vectorfunctie \(\mathbf{r}(t)=f(t)\,\mathbf{i}+g(t)\,\mathbf{j}+h(t)\,\mathbf{k}\) met \(a\leq t\leq b\) heet een parametrisering van de kromme \(\mathcal{C}\).

Voorbeeld: Parametriseringen van de hlave cirkel \(x^2+y^2=1\) met \(y\geq0\) zijn:

1. \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) met \(0\leq t\leq\pi\);


2. \(\mathbf{r}(t)=t\,\mathbf{i}+\sqrt{1-t^2}\,\mathbf{j}\) met \(-1\leq t\leq1\);


3. \(\mathbf{r}(t)=-t\,\mathbf{i}+\sqrt{1-t^2}\,\mathbf{j}\) met \(-1\leq t\leq1\);


4. \(\mathbf{r}(t)=(1-t)\,\mathbf{i}+\sqrt{2t-t^2}\,\mathbf{j}\) met \(0\leq t\leq2\).

De booglengte van een kromme

Definitie: Laat \(\mathcal{C}\) een kromme zijn gedefinieerd door de vectorfunctie \(\mathbf{r}(t)\) met \(a\leq t\leq b\). Als de kromme \(\mathcal{C}\) precies één keer wordt doorlopen als \(t\) toeneemt van \(a\) tot \(b\), dan is

\[L=\int\limits_{\mathcal{C}}ds=\int_a^b|\mathbf{r}'(t)|\,dt\]

de booglengte van de kromme \(\mathcal{C}\).

Voorbeelden:

1) Bepaal de omtrek van een cirkel met straal \(1\), dat wil zeggen, de booglengte van de kromme \(\mathcal{C}:\;\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) met \(0\leq t\leq 2\pi\).

Oplossing: \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) en dus \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2}=1\). Dus:

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=\int_0^{2\pi}1\,dt=2\pi.\]

2) Bepaal de lengte van de boog van de cirkelvormige helix gegeven door \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+t\,\mathbf{k}\) met \(0\leq t\leq 2\pi\).

Oplossing: \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}+1\,\mathbf{k}\) en dus \(|\mathbf{r}'(t)=\sqrt{(-\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{2}\). Dus:

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=\int_0^{2\pi}\sqrt{2}\,dt=2\pi\sqrt{2}.\]

Definitie: Laat \(\mathcal{C}\) een kromme zijn gedefinieerd door de vectorfunctie \(\mathbf{r}(t)\) met \(a\leq t\leq b\). Als \(\mathbf{r}'\) continu is en \(\mathcal{C}\) wordt precies één keer doorlopen als \(t\) toeneemt van \(a\) tot \(b\), dan is

\[s(t)=\int_a^t|\mathbf{r}'(u)|\,du\]

de booglengtefunctie van de kromme \(\mathcal{C}\).

De functie \(s(t)=\displaystyle\int_a^t|\mathbf{r}'(u)|\,du\) is de booglengte van het deel van de kromme \(\mathcal{C}\) tussen \(\mathbf{r}(a)\) en \(\mathbf{r}(t)\). Merk op dat \(\displaystyle\frac{ds}{dt}=|\mathbf{r}'(t)|\).

Toepassingen: we beschouwen de booglengte van een kettinglijn, een cycloïde en een cardioïde.

1) De grafiek van een flexibele ketting heet een kettinglijn en wordt, bijvoorbeeld, gegeven door de parametrisering \(\mathbf{r}(t)=t\,\mathbf{i}+\cosh(t)\,\mathbf{j}\) met \(0\leq t\leq 2\).

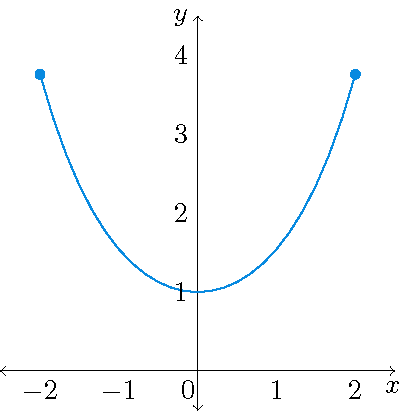
De functie \(\cosh\) heet cosinus hyperbolicus en wordt gedefinieerd als: \(\cosh(x)=\displaystyle\frac{e^x+e^{-x}}{2}\).

We hebben ook de sinus hyperbolicus en de tangens hyperbolicus gedefinieerd door

\[\sinh(x)=\frac{e^x-e^{-x}}{2}\quad\textrm{en}\quad\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}.\]

Zie ook: Stewart §3.11.

Merk op dat geldt:

\[\sinh(-x)=-\sinh(x),\quad\cosh(-x)=\cosh(x)\quad\textrm{en}\quad\tanh(-x)=-\tanh(x).\]

Verder geldt

\[\sinh'(x)=\cosh(x),\quad\cosh'(x)=\sinh(x)\quad\textrm{en}\quad\cosh^2(x)-\sinh^2(x)=1.\]

Voor de booglengte van de kettinglijn volgt nu:

\begin{align*} L&=\int_{-2}^2|\mathbf{r}'(t)|\,dt=\int_{-2}^2\sqrt{1+\sinh^2(t)}\,dt=\int_{-2}^2\sqrt{\cosh^2(t)}\,dt=\int_{-2}^2\cosh(t)\,dt\\[2.5mm] &=\sinh(t)\bigg|_{-2}^2=\sinh(2)-\sinh(-2)=2\sinh(2)=e^2-e^{-2}\approx7.254. \end{align*} 2) De kromme die wordt beschreven door een punt \(P\) op de rand van een cirkel als de cirkel rolt langs een rechte lijn heet een cycloïde (zie ook: Stewart §10.1 en §10.2). Als de cirkel straal \(r\) heeft, deze rolt langs de \(x\)-as en als het punt door de oorsprong gaat, dan is een parametrisering van deze cycloïde gelijk aan

\[\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j},\quad 0\leq t\leq 2\pi.\]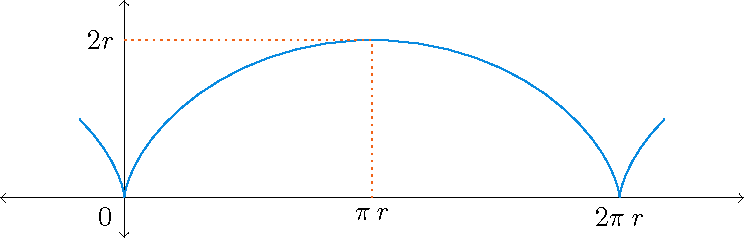

Merk op dat

\[\mathbf{r}'(t)=r(1-\cos(t))\,\mathbf{i}+r\sin(t)\,\mathbf{j},\]

hetgeen leidt tot de booglengte

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=r\int_0^{2\pi}\sqrt{(1-\cos(t))^2+(\sin(t))^2}\,dt=r\int_0^{2\pi}\sqrt{2-2\cos(t)}\,dt.\]

Nu gebruiken we

\[\cos(2x)=\cos^2(x)-\sin^2(x)=1-2\sin^2(x)\quad\Longrightarrow\quad2\sin^2(x)=1-\cos(2x)\]

en vinden dat

\[L=r\int_0^{2\pi}\sqrt{2-2\cos(t)}\,dt=r\int_0^{2\pi}\sqrt{4\sin^2\left(\tfrac{t}{2}\right)}\,dt =2r\int_0^{2\pi}\left|\sin\left(\tfrac{t}{2}\right)\right|\,dt=2r\int_0^{2\pi}\sin\left(\tfrac{t}{2}\right)\,dt =2r\bigg[-2\cos\left(\tfrac{t}{2}\right)\bigg]_{t=0}^{2\pi}=8r.\]

3) Beschouw de cardioïde die in poolcoördinaten wordt gegeven door \(r=2+2\cos(\theta)\):

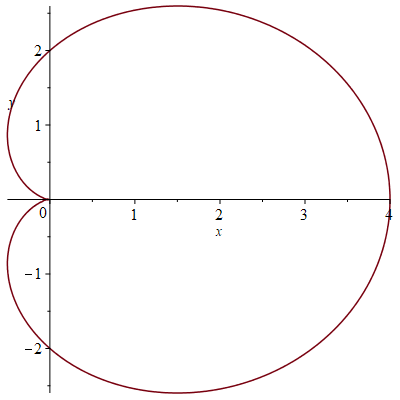
Hieruit volgt dat

\[\mathbf{r}(t)=(2+2\cos(t))\cos(t)\,\mathbf{i}+(2+2\cos(t))\sin(t)\,\mathbf{j},\quad 0\leq t\leq 2\pi\]

een parametrisering van deze cardioïde is. De booglengte is dus gelijk aan \(L=\displaystyle\int_0^{2\pi}|\mathbf{r}'(t)|\,dt\), waarbij

\[\mathbf{r}'(t)=\langle -(2+2\cos(t))\sin(t)-2\sin(t)\cos(t),(2+2\cos(t))\cos(t)-2\sin^2(t) \rangle.\]

Dus geldt

\begin{align*} \mathbf{r}'(t)|^2&=(2+2\cos(t))^2\sin^2(t)+4(2+2\cos(t))\sin^2(t)\cos(t)+4\sin^2(t)\cos^2(t)\\[2.5mm] &{}\hspace{25mm}+(2+2\cos(t))^2\cos^2(t)-4(2+2\cos(t))\sin^2(t)\cos(t)+4\sin^4(t)\\[2.5mm] &=(2+2\cos(t))^2(\sin^2(t)+\cos^2(t))+4\sin^2(t)(\cos^2(t)+\sin^2(t))\\[2.5mm] &=(2+2\cos(t))^2+4\sin^2(t)=4+8\cos(t)+4\cos^2(t)+4\sin^2(t)=8+8\cos(t) \end{align*}

en dus

\[L=\int_0^{2\pi}\sqrt{8+8\cos(t)}\,dt=2\int_0^{\pi}\sqrt{8+8\cos(t)}\,dt=4\sqrt{2}\int_0^{\pi}\sqrt{1+\cos(t)}\,dt.\]

Merk op dat voor \(0 < t \leq \pi\) geldt

\[\sqrt{1+\cos(t)}=\sqrt{1+\cos(t)}\cdot\frac{\sqrt{1-\cos(t)}}{\sqrt{1-\cos(t)}}=\frac{\sqrt{1-\cos^2(t)}}{\sqrt{1-\cos(t)}} =\frac{\sqrt{\sin^2(t)}}{\sqrt{1-\cos(t)}}=\frac{|\sin(t)|}{\sqrt{1-\cos(t)}}=\frac{\sin(t)}{\sqrt{1-\cos(t)}}.\]

Dus geldt

\[L=4\sqrt{2}\int_0^{\pi}\frac{\sin(t)}{\sqrt{1-\cos(t)}}\,dt=8\sqrt{2}\,\sqrt{1-\cos(t)}\bigg|_0^{\pi}=8\sqrt{2}\cdot\sqrt{2}=16.\]

---

Laatst gewijzigd op 9 oktober 2021