Analyse – Vectoranalyse – Oppervlakintegralen

De oppervlakintegraal van een scalaire functie

Neem aan dat \(f\) een functie is van drie variabelen waarvan het domein een oppervlak \(S\) bevat gegeven door de vectorfunctie

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D.\]

We nemen eerst aan dat \(D\) een rechthoek is en we verdelen het in deelrechthoeken \(R_{ij}\) met afmetingen \(\Delta u\) en \(\Delta v\). Dan wordt het oppervlak \(S\) verdeeld in corresponderende patches \(S_{ij}\). We berekenen \(f\) in het punt \(P_{ij}^*\) in elke patch, vermenigvuldigen met de oppervlakte \(\Delta S_{ij}\) van de patch en vormen de Riemannsom

\[\sum_{i=1}^m\sum_{j=1}^nf(P_{ij}^*)\Delta S_{ij}.\]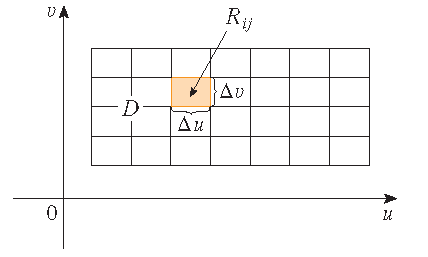

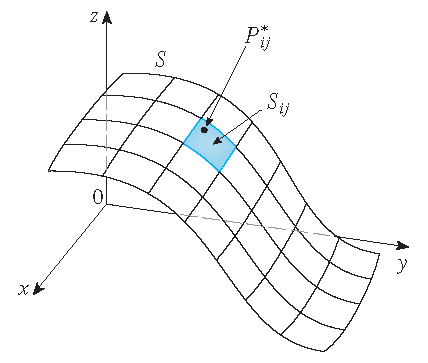Dan nemen we de limiet als het aantal patches toeneemt en definiëren de oppervlakintegraal van \(f\) over het oppervlak \(S\) als

\[\iint\limits_Sf(x,y,z)\,dS=\lim\limits_{m\to\infty}\lim\limits_{n\to\infty}\sum_{i=1}^m\sum_{j=1}^nf(P_{ij}^*)\Delta S_{ij}.\]

Merk op dat het speciale geval \(f(x,y,z)=1\) de oppervlakte van het oppervlak \(S\) definieert. We vervolgen daarom op dezelfde manier door de oppervlakte van de patch \(S_{ij}\) te benaderen door de oppervlakte van een benaderend parallellogram in het raakvlak.

Definitie: Als \(S\) een glad parameteroppervlak is gegeven door

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D\]

en \(S\) wordt precies één keer doorlopen als \((u,v)\) door het parameterdomein \(D\) loopt, dan is de oppervlakintegraal van \(f\) over het oppervlak \(S\) gelijk aan

\[\iint\limits_Sf(x,y,z)\,dS=\iint\limits_Df(\mathbf{r}(u,v))\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA,\]

waarbij \(\displaystyle\mathbf{r}_u=\frac{\partial x}{\partial u}\,\mathbf{i}+\frac{\partial y}{\partial u}\,\mathbf{j}+\frac{\partial z}{\partial u}\,\mathbf{k}\) en \(\displaystyle\mathbf{r}_v=\frac{\partial x}{\partial v}\,\mathbf{i}+\frac{\partial y}{\partial v}\,\mathbf{j}+\frac{\partial z}{\partial v}\,\mathbf{k}\).

Stewart §16.7, Voorbeeld 1
Bereken de oppervlakintegraal \(\displaystyle\iint\limits_Sx^2\,dS\), waarbij \(S\) is de eenheidsbol \(x^2+y^2+z^2=1\) is.

Oplossing: Een parametrisering van \(S\) is

\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq\pi,\quad 0\leq\theta\leq 2\pi.\]

Dan geldt als eerder

\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\quad\Longrightarrow\quad \left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|=\sin(\phi)\geq 0.\]

Dus volgt met \(D=\{(\phi,\theta)\,|\,0\leq\phi\leq\pi,\;0\leq\theta\leq2\pi\}\)

\begin{align*} \iint\limits_Sx^2\,dS&=\iint\limits_D\sin^2(\phi)\cos^2(\theta)\,\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|\,dA =\int_0^{2\pi}\int_0^{\pi}\sin^3(\phi)\cos^2(\theta)\,d\phi\,d\theta=\int_0^{2\pi}\cos^2(\theta)\,d\theta\,\int_0^{\pi}\sin^3(\phi)\,d\phi\\[2.5mm] &=\frac{1}{2}\int_0^{2\pi}\left(1+\cos(2\theta)\right)\,d\theta\,\int_0^{\pi}\sin(\phi)\left(1-\cos^2(\phi)\right)\,d\phi =\frac{1}{2}\bigg[\theta+\frac{1}{2}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}\,\bigg[-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\bigg]_{\phi=0}^{\pi}\\[2.5mm] &=\frac{1}{2}\cdot2\pi\cdot\frac{4}{3}=\frac{4}{3}\pi. \end{align*}

Toepassing: fysische interpretatie

Neem aan dat \(\rho(x,y,z)\geq 0\) een massadichtheidsfunctie is gedefinieerd in de punten \((x,y,z)\) van een dun vel (zeg, van aluminiumfolie) in de vorm van een oppervlak \(S\). Dan is

\[m=\iint\limits_S\rho(x,y,z)\,dS\]

de (totale) massa van het vel. Verder geldt: het massamiddelpunt \((\overline{x},\overline{y},\overline{z})\) wordt gegeven door

\[\overline{x}=\frac{1}{m}\iint\limits_Sx\,\rho(x,y,z)\,dS,\quad\overline{y}=\frac{1}{m}\iint\limits_Sy\,\rho(x,y,z)\,dS \quad\textrm{en}\quad\overline{z}=\frac{1}{m}\iint\limits_Sz\,\rho(x,y,z)\,ds.\]

Stewart §16.7, Voorbeeld 2
Bereken \(\displaystyle\iint\limits_Sy\,dS\), waarbij \(S\) het oppervlak \(z=x+y^2\) is met \(0\leq x\leq 1\) en \(0\leq y\leq 2\).

Oplossing: Merk op dat het oppervlak \(S\) de grafiek is van een functie van twee variabelen:

\[S:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x+y^2)\,\mathbf{k}\]

met domein \(D=[0,1]\times[0,2]=\{(x,y)\,|\,0\leq x\leq 1,\;0\leq y\leq 2\}\). Dus geldt

\[\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,1\rangle\times\langle 0,1,2y\rangle=\langle -1,-2y,1\rangle\quad\Longrightarrow\quad \left|\mathbf{r}_x\times\mathbf{r}_y\right|=\sqrt{(-1)^2+(-2y)^2+1}=\sqrt{2+4y^2}\]

en dus

\[\iint\limits_Sy\,dS=\iint\limits_Dy\sqrt{2+4y^2}\,dA=\int_0^1\,dx\,\int_0^2y\sqrt{2+4y^2}\,dy =1\cdot\bigg[\frac{1}{12}(2+4y^2)^{3/2}\bigg]_{y=0}^2=\frac{1}{12}\left(54\sqrt{2}-2\sqrt{2}\right)=\frac{13}{3}\sqrt{2}.\]

Stuksgewijs gladde oppervlakken

Als \(S\) een stuksgewijs glad oppervlak is, dat wil zeggen, een eindige vereniging van galdde oppervlakken \(S_1,S_2,\ldots,S_n\) die elkaar alleen snijden langs de randen, dan wordt de oppervlakintegraal van \(f\) over \(S\) gedefinieerd door

\[\iint\limits_Sf(x,y,z)\,dS=\iint\limits_{S_1}f(x,y,z)\,dS+\iint\limits_{S_2}f(x,y,z)\,dS+\cdots+\iint\limits_{S_n}f(x,y,z)\,dS.\]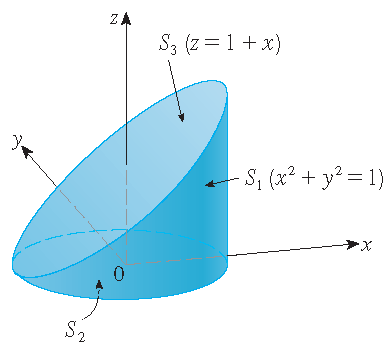

Stewart §16.7, Voorbeeld 3
Bereken \(\displaystyle\iint\limits_Sz\,dS\), waarbij \(S\) het oppervlak is waarvan de zijde \(S_1\) wordt bepaald door de cilinder \(x^2+y^2=1\), de bodem \(S_2\) de cirkelschijf \(x^2+y^2\leq 1\) in het vlak \(z=0\) is en waarvan de bovenkant \(S_3\) i het deel is van het vlak \(z=1+x\) dat boven \(S_2\) ligt.

Oplossing: Het oppervlak \(S\) wordt getoond in het plaatje. Voor \(S_1\) gebruiken we \(\theta\) en \(z\) als parameters:

\[S_1:\;\mathbf{r}(\theta,z)=\cos(\theta)\,\mathbf{i}+\sin(\theta)\,\mathbf{j}+z\,\mathbf{k},\]

waarbij \(0\leq\theta\leq2\pi\) en \(0\leq z\leq 1+x=1+\cos(\theta)\). Dus

\[\mathbf{r}_{\theta}\times\mathbf{r}_z=\langle -\sin(\theta),\cos(\theta),0 \rangle\times\langle 0,0,1\rangle =\langle \cos(\theta),\sin(\theta),0 \rangle\quad\Longrightarrow\quad\left|\mathbf{r}_{\theta}\times\mathbf{r}_z\right| =\sqrt{\cos^2(\theta)+\sin^2(\theta)+0}=1.\]

Dus volgt met \(D=\{(\theta,z)\,|\,0\leq\theta\leq2\pi,\;0\leq z\leq 1+\cos(\theta)\}\)

\begin{align*} \iint\limits_{S_1}z\,dS&=\iint\limits_Dz\,\left|\mathbf{r}_{\theta}\times\mathbf{r}_z\right|\,dA =\int_0^{2\pi}\int_0^{1+\cos(\theta)}z\,dz\,d\theta=\frac{1}{2}\int_0^{2\pi}\left(1+\cos(\theta)\right)^2\,d\theta\\[2.5mm] &=\frac{1}{2}\int_0^{2\pi}\left(1+2\cos(\theta)+\frac{1}{2}\left(1+\cos(2\theta)\right)\right)\,d\theta =\frac{1}{2}\bigg[\frac{3}{2}\theta+2\sin(\theta)+\frac{1}{4}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}=\frac{3}{2}\pi. \end{align*}

Omdat \(S_2\) in het vlak \(z=0\) ligt geldt: \(\displaystyle\iint\limits_{S_2}z\,dS=0\).

Het bovenste oppervlak \(S_3\) ligt boven de eenheidscirkelschijf \(x^2+y^2\leq 1\) en is deel van het vlak \(z=1+x\) dat de grafiek is van een functie van twee variabelen:

\[S_3:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(1+x)\,\mathbf{k},\quad x^2+y^2\leq 1.\]

Dan geldt

\[\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,1 \rangle\times\langle 0,1,0\rangle=\langle -1,0,1\rangle\quad\Longrightarrow\quad \left|\mathbf{r}_x\times\mathbf{r}_y\right|=\sqrt{(-1)^2+0+1}=\sqrt{2}\]

en dus volgt, met behulp van poolcoördinaten,

\begin{align*} \iint\limits_{S_3}z\,dS&=\iint\limits_{x^2+y^2\leq1}(1+x)\,\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA =\int_0^{2\pi}\int_0^1(1+r\,\cos(\theta))\,\sqrt{2}\,r\,dr\,d\theta=\sqrt{2}\int_0^{2\pi}\int_0^1\left(r+r^2\cos(\theta)\right)\,dr\,d\theta\\[2.5mm] &=\sqrt{2}\int_0^{2\pi}\bigg[\frac{1}{2}r^2+\frac{1}{3}r^3\cos(\theta)\bigg]_{r=0}^1\,d\theta =\sqrt{2}\int_0^{2\pi}\left(\frac{1}{2}+\frac{1}{3}\cos(\theta)\right)\,d\theta =\sqrt{2}\bigg[\frac{1}{2}\theta+\frac{1}{3}\sin(\theta)\bigg]_{\theta=0}^{2\pi}=\pi\sqrt{2}. \end{align*}

Ten slotte concluderen we dat

\[\iint\limits_Sz\,dS=\iint\limits_{S_1}z\,dS+\iint\limits_{S_2}z\,dS+\iint\limits_{S_3}z\,dS =\frac{3}{2}\pi+0+\pi\sqrt{2}=\left(\frac{3}{2}+\sqrt{2}\right)\pi.\]

Oriënteerbare oppervlakken

Een oriënteerbaar oppervlak heeft twee kanten. Een voorbeeld van een niet-oriënteerbaar oppervlak is de Möbius band, genoemd naar de Duitse wiskundige August Ferdinand Möbius (1790-1868):

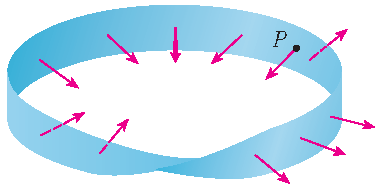
Men kan deze construeren door een lange strook papier te nemen,

deze een halve draai te geven en de korte uiteinden aan elkaar te plakken:

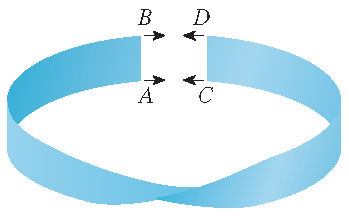
Zo'n Möbius band heeft echt maar één kant.

Georiënteerde oppervlakken

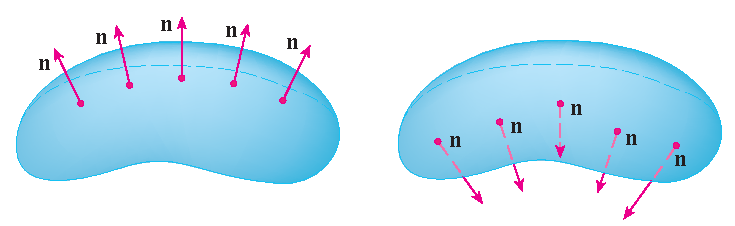
Vanaf nu beschouwen we alleen oriënteerbare (tweezijdige) oppervlakken. Zo mogelijk kiezen we een eenheidsnormaalvector \(\mathbf{n}\) in elk punt \((x,y,z)\) op zo'n oppervlak zodat \(\mathbf{n}\) continu varieert over \(S\), dan heet \(S\) een georiënteerd oppervlak en de bepaalde keuze van \(\mathbf{n}\) voorziet \(S\) van een oriëtatie. Er zijn twee mogelijke oriëntaties voor elk oriënteerbaar oppervlak:

Beschouw een oriënteerbaar parameteroppervlak

\[S:\;\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad(u,v)\in D\]

met raakvectoren \(\mathbf{r}_u\) en \(\mathbf{r}_v\). Dan induceert de parametrisering een oriëntatie bepaald door \(\displaystyle\mathbf{n}=\frac{\mathbf{r}_u\times\mathbf{r}_v}{\left|\mathbf{r}_u\times\mathbf{r}_v\right|}\) en de tegengestelde oriëntatie wordt bepaald door \(-\mathbf{n}\).

We hebben bijvoorbeeld gezien dat

\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k}\]

met domein \(0\leq\phi\leq\pi\) en \(0\leq\theta\leq2\pi\) een parametervoorstelling is voor de bol \(x^2+y^2+z^2=a^2\) met \(a\geq0\). Dan geldt

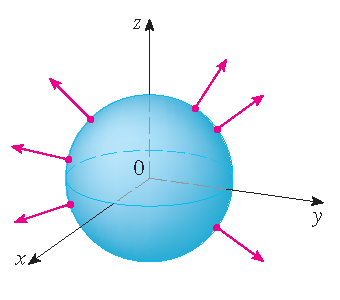
\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=a\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\quad\Longrightarrow\quad \mathbf{n}=\frac{\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}}{\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|} =\frac{1}{a}\cdot\mathbf{r}(\phi,\theta).\]

Merk op dat \(\mathbf{n}\) in dezelfde richting wijst als de plaatsvector \(\mathbf{r}(\phi,\theta)\), dat wil zeggen, naar buiten gericht vanuit de bol. De tegengestelde (naar binnen) gerichte oriëntatie zouden we krijgen als we de volgorde van de raakvectoren zouden verwisselen omdat \(\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}=-\left(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right)\).

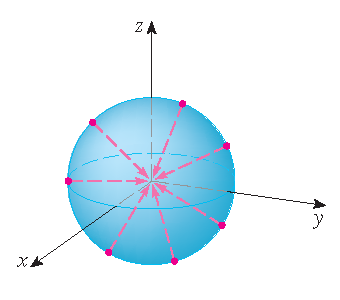positive orientation	negative orientation

Voor een gesloten oppervlak, dat wil zeggen, een oppervlak dat de rand is van een lichaam \(E\), is de conventie dat de positieve oriëntatie degene is waarvan de normaalvectoren naar buiten wijzen vanuit \(E\) en de naar binnen wijzende normalen geven de negatieve oriëntatie.

De oppervlakintegraal van een vectorveld

Definitie: Als \(\mathbf{F}\) een continu vectorveld is gedefinieerd op een georiënteerd oppervlak \(S\) met eenheidsnormaalvector \(\mathbf{n}\), dan is

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_S\mathbf{F}\cdot\mathbf{n}\,dS\]

de oppervlakintegraal van \(\mathbf{F}\) over het oopervlak \(S\). Deze integraal heet ook wel de flux van \(\mathbf{F}\) door \(S\).

De oppervlakintegraal van een vectorveld over \(S\) is gelijk aan de oppervlakintegraal van de normale component over \(S\). Als \(S\) wordt gegeven door de parametrisering

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad(u,v)\in D\]

waarbij \(D\) het parameterdomein is, dan geldt

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_D\mathbf{F}(\mathbf{r}(u,v))\cdot\left(\mathbf{r}_u\times\mathbf{r}_v\right)\,dA,\]

want \(\mathbf{n}=\displaystyle\frac{\mathbf{r}_u\times\mathbf{r}_v}{\left|\mathbf{r}_u\times\mathbf{r}_v\right|}\) en \(dS=\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA\).

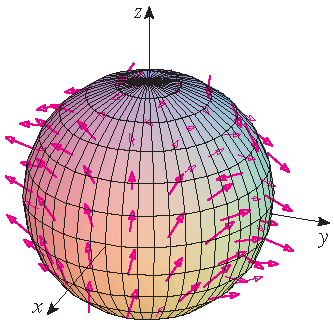
Stewart §16.7, Voorbeeld 4
Bepaal de flux van het vectorveld \(\mathbf{F}(x,y,z)=z\,\mathbf{i}+y\,\mathbf{j}+x\,\mathbf{k}\) door de eenheidsbol \(x^2+y^2+z^2=1\).

Oplossing: We gebruiken de parametrisering

\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k}\]

met domein \(0\leq\phi\leq\pi\) en \(0\leq\theta\leq2\pi\) voor de eenheidsbol. Dan geldt

\[\mathbf{r}_{\phi}\times\mathbf{\theta}=\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\]

en dus

\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\iint\limits_D\mathbf{F}(\mathbf{r}(\phi,\theta))\cdot\left(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right)\,dA =\int_0^{2\pi}\int_0^{\pi}\langle\cos(\phi),\sin(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\theta)\rangle\cdot\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(\sin^2(\phi)\cos(\phi)\cos(\theta)+\sin^3(\phi)\sin^2(\theta)+\sin^2(\phi)\cos(\phi)\cos(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\cos(\theta)\,d\theta\,\int_0^{\pi}2\sin^2(\phi)\cos(\phi)\,d\phi+\int_0^{2\pi}\sin^2(\theta)\,d\theta\,\int_0^{\pi}\sin^3(\phi)\,d\phi\\[2.5mm] &=\bigg[\sin(\theta)\bigg]_{\theta=0}^{2\pi}\bigg[\frac{1}{3}\sin^3(\phi)\bigg]_{\phi=0}^{\pi} +\bigg[\frac{1}{2}\theta-\frac{1}{2}\cos(2\theta)\bigg]_{\theta=0}^{2\pi}\bigg[-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\bigg]_{\phi=0}^{\pi} =0+\pi\cdot\frac{4}{3}=\frac{4}{3}\pi. \end{align*}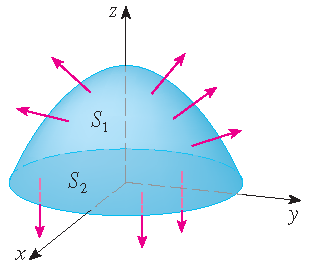

Voorbeeld (vergelijk met Stewart §16.7, Voorbeeld 5)
Bereken \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}\), waarbij \(\mathbf{F}(x,y,z)=y\,\mathbf{i}+x\,\mathbf{j}+(z+1)\,\mathbf{k}\) en \(S\) is de rand van het lichaam \(E\) ingesloten door de paraboloïde \(z=1-x^2-y^2\) en het vlak \(z=0\).

Oplossing: Het oppervlak \(S\) bestaat uit een parabolisch oppervlak \(S_1\) aan de bovenkant en een cirkelvormige bodem \(S_2\). Omdat \(S\) een gesloten oppervlak is, gebruiken we de conventie van positieve (naar buiten gerichte) oriëntatie. Dat betekent dat \(S_1\) naar boven georiënteerd is. Merk op dat \(S_1\) de garfiek is van een functie van twee variabelen:

\[S_1:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(1-x^2-y^2)\,\mathbf{k},\quad x^2+y^2\leq 1\]

met \(\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,-2x\rangle\times\langle 0,1,-2y\rangle=\langle 2x,2y,1\rangle\), die naar boven gericht is. Dus volgt met behulp van poolcoördinaten

\begin{align*} \iint\limits_{S_1}\mathbf{F}\cdot d\mathbf{S}&=\iint\limits_{x^2+y^2\leq1}\langle y,x,2-x^2-y^2\rangle\cdot\langle 2x,2y,1\rangle\,dA =\iint\limits_{x^2+y^2\leq1}\left(2xy+2xy+2-x^2-y^2\right)\,dA\\[2.5mm] &=\int_0^{2\pi}\int_0^1\left(4r^2\cos(\theta)\sin(\theta)+2-r^2\right)\,r\,dr\,d\theta =\int_0^{2\pi}\bigg[r^4\cos(\theta)\sin(\theta)+r^2-\frac{1}{4}r^4\bigg]_{r=0}^1\,d\theta\\[2.5mm] &=\int_0^{2\pi}\left(\cos(\theta)\sin(\theta)+\frac{3}{4}\right)\,d\theta =\bigg[\frac{1}{2}\sin^2(\theta)+\frac{3}{4}\theta\bigg]_{\theta=0}^{2\pi}=\frac{3}{2}\pi. \end{align*}

Een parametrisering van \(S_2\) is bijvoorbeeld

\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+0\,\mathbf{k},\quad x^2+y^2\leq 1\]

met \(\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,0\rangle\times\langle 0,1,0\rangle=\langle 0,0,1\rangle\), die naar boven gericht is. De positieve (naar buiten gerichte) oriëntatie zou naar beneden gericht moeten zijn op \(S_2\), dus volgt

\[\iint\limits_{S_2}\mathbf{F}\cdot d\mathbf{S}=-\iint\limits_{x^2+y^2\leq1}\langle y,x,1\rangle\cdot\langle 0,0,1\rangle\,dA =-\iint\limits_{x^2+y^2\leq1}1\,dA=-\pi.\]

We concluderen dat

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_{S_1}\mathbf{F}\cdot d\mathbf{S}+\iint\limits_{S_2}\mathbf{F}\cdot d\mathbf{S} =\frac{3}{2}\pi-\pi=\frac{1}{2}\pi.\]

---

Laatst gewijzigd op 18 oktober 2021