Analyse – Vectoranalyse – De divergentiestelling van Gauss
Definitie: Een gebied \(D\) in \(\mathbb{R}^3\) heet een regulier gebied als het van type 1, van type 2 en van type 3 is.
Stelling: Laat \(E\) een regulier gebied zijn en laat \(S\) het gesloten randoppervlak van \(E\) zijn met positieve (naar buiten gerichte) oriëntatie. Laat \(\mathbf{F}\) een vectorveld zijn waarvan de componentfuncties continue partiële afgeleiden hebben op een open gebied dat \(E\) bevat. Dan geldt
\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV.\]Bewijs: Stel dat \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\). Dan geldt
\[\textrm{div}\,\mathbf{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\]en dus
\[\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E\frac{\partial P}{\partial x}\,dV+\iiint\limits_E\frac{\partial Q}{\partial y}\,dV +\iiint\limits_E\frac{\partial R}{\partial z}\,dV.\]Als \(\mathbf{n}\) de eenheidsnormaal is van \(E\), dan is de oppervlakintegraal gelijk aan
\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_S\mathbf{F}\cdot\mathbf{n}\,dS =\iint\limits_S\left(P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\right)\cdot\mathbf{n}\,dS =\iint\limits_SP\,\mathbf{i}\cdot\mathbf{n}\,dS+\iint\limits_SQ\,\mathbf{j}\cdot\mathbf{n}\,dS+\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS\]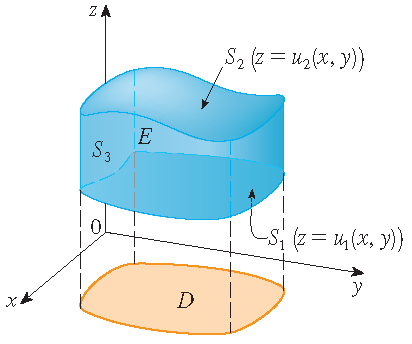
Merk op dat \(E\) een type 1 gebied is, dus \(E=\{(x,y,z)\,|\,(x,y)\in D,\;u_1(x,y)\leq z\leq u_2(x,y)\}\), waarbij \(D\) de projectie is van \(E\) op het \(xy\)-vlak. Dan geldt
\[\iiint\limits_E\frac{\partial R}{\partial z}\,dV=\iint\limits_D\left(\int_{u_1(x,y)}^{u_2(x,y)}\frac{\partial R}{\partial z}\,dz\right)\,dA =\iint\limits_D\left(R(x,y,u_2(x,y))-R(x,y,u_1(x,y))\right)\,dA.\]Het randoppervlak \(S\) bestaat uit drie delen; het oppervlak \(S_1\) aan de onderkant, het oppervlak \(S_2\) aan de bovenkant en eventueel een verticaal oppervlak \(S_3\), dat boven de randkromme van \(D\) ligt. Het zou kunnen dat er helemaal geen \(S_3\) is (zoals in het geval van een bol bijvoorbeeld). Merk op dat op \(S_3\) geldt dat \(\mathbf{k}\cdot\mathbf{n}=0\), want \(\mathbf{k}\) is verticaal en \(\mathbf{n}\) is horizontaal, dus
\[\iint\limits_{S_3}R\,\mathbf{k}\cdot\mathbf{n}\,dS=0.\]Dus, of er nu wel of niet een verticaal oppervlak is, geldt
\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS+\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS.\]Een parametrisering van \(S_2\) is \(\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+u_2(x,y)\,\mathbf{k}\) met \((x,y)\in D\) en de naar buiten gerichte normaal \(\mathbf{n}\) is naar boven gericht, dus volgt
\[\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_DR(x,y,u_2(x,y))\,dA.\]Evenzo; een parametrisering van \(S_1\) is \(\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+u_1(x,y)\,\mathbf{k}\) met \((x,y)\in D\), maar hier is de naar buiten gerichte normaal \(\mathbf{n}\) naar beneden gericht, dus volgt
\[\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS=-\iint\limits_DR(x,y,u_1(x,y))\,dA.\]Dus geldt dat
\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS+\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS =\iint\limits_D\left(R(x,y,u_2(x,y))-R(x,y,u_1(x,y))\right)\,dA.\]Dit bewijst dat
\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial R}{\partial z}\,dV.\]Evenzo kunnen we bewijzen dat \(\displaystyle\iint\limits_SP\,\mathbf{i}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial P}{\partial x}\,dV\) en \(\displaystyle\iint\limits_SQ\,\mathbf{j}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial Q}{\partial y}\,dV\) door te gebruiken dat \(E\) ook een gebied van type 2 en van type 3 is, respectievelijk.
Stewart §16.9, Voorbeeld 1
Bepaal de flux van het vectorveld \(\mathbf{F}(x,y,z)=z\,\mathbf{i}+y\,\mathbf{j}+x\,\mathbf{k}\) door de eenheidsbol \(x^2+y^2+z^2=1\).
Oplossing: Merk op dat \(\textrm{div}\,\mathbf{F}=0+1+0=1\). De eenheidsbol \(S\) is de gesloten rand van de eenheidsbol \(E\) gegeven door \(x^2+y^2+z^2\leq1\). Dus, toepassing van de divergentiestelling van Gauss leidt tot de flux
\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E1\,dV=\textrm{vol}(E)=\frac{4}{3}\pi.\]Voor een rechtstreekse berekening van de fluxintegraal zouden we de parametrisering
\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq\pi,\quad 0\leq\theta\leq2\pi\]met \(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=\sin(\phi)\,\mathbf{r}(\phi,\theta)\) kunnen gebruiken en vinden dan
\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\int_0^{2\pi}\int_0^{\pi}\langle\cos(\phi),\sin(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\theta)\rangle \cdot\langle\sin^2(\phi)\,\cos(\theta),\sin^2(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\phi)\rangle\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)+\sin^3(\phi)\,\sin^2(\theta)+\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(2\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)+\sin(\phi)\left(1-\cos^2(\phi)\right)\,\sin^2(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\bigg[\frac{2}{3}\sin^3(\phi)\,\cos(\theta)+\left(-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\right)\sin^2(\theta)\bigg]_{\phi=0}^{\pi}\,d\theta =\frac{4}{3}\int_0^{2\pi}\sin^2(\theta)\,d\theta\\[2.5mm] &=\frac{2}{3}\int_0^{2\pi}\left(1-\cos(2\theta)\right)\,d\theta=\frac{2}{3}\bigg[\theta-\frac{1}{2}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}=\frac{4}{3}\pi, \end{align*}hetgeen veel omslachtiger is.
 Stewart §16.9, Voorbeeld 2
Stewart §16.9, Voorbeeld 2
Bereken \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}\), waarbij
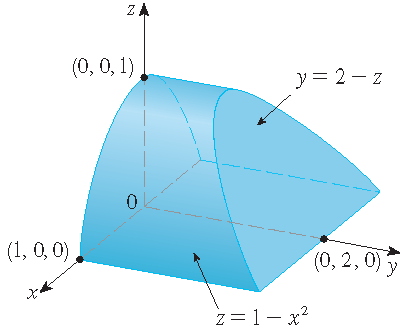
en \(S\) het randoppervlak is van het gebied \(E\) begrensd door de parabolische cilinder \(z=1-x^2\) en de vlakken \(z=0\), \(y=0\) en \(y+z=2\).
Oplossing: Het zou extreem lastig zijn om de gegeven oppervlakintegraal rechtstreeks te berekenen. Echter, er geldt
\[\textrm{div}\,\mathbf{F}=\frac{\partial}{\partial x}(xy)+\frac{\partial}{\partial y}\left(y^2+e^{xz^2}\right)+\frac{\partial}{\partial z}\sin(xy) =y+2y+0=3y.\]Nu leidt toepassing van de divergentiestelling van Gauss tot \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV\), waarbij
\[E=\{(x,y,z)\,|\,-1\leq x\leq 1,\;0\leq z\leq 1-x^2,\;0\leq y\leq 2-z\}.\]Dus geldt
\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E3y\,dS =3\int_{-1}^1\int_0^{1-x^2}\int_0^{2-z}y\,dy\,dz\,dx=\frac{3}{2}\int_{-1}^1\int_0^{1-x^2}(2-z)^2\,dz\,dx\\[2.5mm] &=\frac{3}{2}\int_{-1}^1\bigg[-\frac{1}{3}(2-z)^3\bigg]_{z=0}^{1-x^2}\,dx=\frac{1}{2}\int_{-1}^1\left(8-(1+x^2)^3\right)\,dx =\frac{1}{2}\int_{-1}^1\left(7-3x^2-3x^4-x^6\right)\,dx\\[2.5mm] &=\int_0^1\left(7-3x^2-3x^4-x^6\right)\,dx=\bigg[7x-x^3-\frac{3}{5}x^5-\frac{1}{7}x^7\bigg]_{x=0}^1 =7-1-\frac{3}{5}-\frac{1}{7}=\frac{210-21-5}{35}=\frac{184}{35}. \end{align*}Laatst gewijzigd op 20 oktober 2021
 Onderwijs
Onderwijs

