Calculus – Vector calculus – Gauss's divergence theorem

Definition: A region \(D\) in \(\mathbb{R}^3\) is called a regular region if it is of type 1, of type 2 and of type 3.

Theorem: Let \(E\) be a regular solid region and let \(S\) be the closed boundary surface of \(E\) with positive (outward) orientation. Let \(\mathbf{F}\) be a vector field whose component functions have continuous partial derivatives on an open region that contains \(E\). Then

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV.\]

Proof: Let \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\). Then we have

\[\textrm{div}\,\mathbf{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\]

and therefore

\[\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E\frac{\partial P}{\partial x}\,dV+\iiint\limits_E\frac{\partial Q}{\partial y}\,dV +\iiint\limits_E\frac{\partial R}{\partial z}\,dV.\]

If \(\mathbf{n}\) is the unit outward normal of \(E\), then the surface integral is

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_S\mathbf{F}\cdot\mathbf{n}\,dS =\iint\limits_S\left(P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\right)\cdot\mathbf{n}\,dS =\iint\limits_SP\,\mathbf{i}\cdot\mathbf{n}\,dS+\iint\limits_SQ\,\mathbf{j}\cdot\mathbf{n}\,dS+\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS\]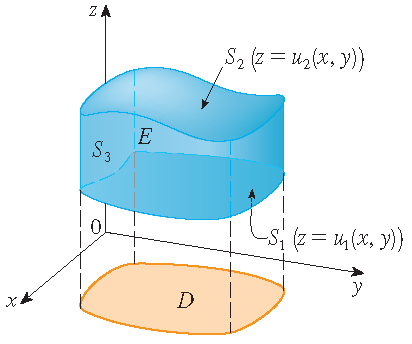

Note that \(E\) is a type 1 region, so \(E=\{(x,y,z)\,|\,(x,y)\in D,\;u_1(x,y)\leq z\leq u_2(x,y)\}\), where \(D\) is the projection of \(E\) onto the \(xy\)-plane. Then we have

\[\iiint\limits_E\frac{\partial R}{\partial z}\,dV=\iint\limits_D\left(\int_{u_1(x,y)}^{u_2(x,y)}\frac{\partial R}{\partial z}\,dz\right)\,dA =\iint\limits_D\left(R(x,y,u_2(x,y))-R(x,y,u_1(x,y))\right)\,dA.\]

The boundary surface \(S\) consists of three parts; the bottom surface \(S_1\), the top surface \(S_2\) and possibly a vertical surface \(S_3\), which lies above the boundary curve of \(D\). It might happen that \(S_3\) doesn't appear (as in the case of a sphere for instance). Note that on \(S_3\) we have \(\mathbf{k}\cdot\mathbf{n}=0\), because \(\mathbf{k}\) is vertical and \(\mathbf{n}\) is horizontal, so

\[\iint\limits_{S_3}R\,\mathbf{k}\cdot\mathbf{n}\,dS=0.\]

Hence, regardless of whether there is vertical surface, we have

\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS+\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS.\]

A parametrization of \(S_2\) is \(\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+u_2(x,y)\,\mathbf{k}\) with \((x,y)\in D\) and the outward normal \(\mathbf{n}\) points upward, so we have

\[\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_DR(x,y,u_2(x,y))\,dA.\]

Similarly, a parametrization of \(S_1\) is \(\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+u_1(x,y)\,\mathbf{k}\) with \((x,y)\in D\), but here the outward normal \(\mathbf{n}\) points downward, so we have

\[\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS=-\iint\limits_DR(x,y,u_1(x,y))\,dA.\]

Therefore we have

\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iint\limits_{S_1}R\,\mathbf{k}\cdot\mathbf{n}\,dS+\iint\limits_{S_2}R\,\mathbf{k}\cdot\mathbf{n}\,dS =\iint\limits_D\left(R(x,y,u_2(x,y))-R(x,y,u_1(x,y))\right)\,dA.\]

This shows that

\[\iint\limits_SR\,\mathbf{k}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial R}{\partial z}\,dV.\]

Similarly we can prove that \(\displaystyle\iint\limits_SP\,\mathbf{i}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial P}{\partial x}\,dV\) and \(\displaystyle\iint\limits_SQ\,\mathbf{j}\cdot\mathbf{n}\,dS=\iiint\limits_E\frac{\partial Q}{\partial y}\,dV\) using the fact that \(E\) is also a region of type 2 and of type 3, respectively.

Stewart §16.9, Example 1
Find the flux of the vector field \(\mathbf{F}(x,y,z)=z\,\mathbf{i}+y\,\mathbf{j}+x\,\mathbf{k}\) over the unit sphere \(x^2+y^2+z^2=1\).

Solution: Note that \(\textrm{div}\,\mathbf{F}=0+1+0=1\). The unit sphere \(S\) is the closed boundary of the unit ball \(E\) given by \(x^2+y^2+z^2\leq1\). So, application of Gauss's divergence theorem leads to the flux

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E1\,dV=\textrm{vol}(E)=\frac{4}{3}\pi.\]

For a direct evaluation of the flux integral we could use the parametrization

\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq\pi,\quad 0\leq\theta\leq2\pi\]

with \(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=\sin(\phi)\,\mathbf{r}(\phi,\theta)\) to obtain

\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\int_0^{2\pi}\int_0^{\pi}\langle\cos(\phi),\sin(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\theta)\rangle \cdot\langle\sin^2(\phi)\,\cos(\theta),\sin^2(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\phi)\rangle\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)+\sin^3(\phi)\,\sin^2(\theta)+\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(2\sin^2(\phi)\,\cos(\phi)\,\cos(\theta)+\sin(\phi)\left(1-\cos^2(\phi)\right)\,\sin^2(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\bigg[\frac{2}{3}\sin^3(\phi)\,\cos(\theta)+\left(-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\right)\sin^2(\theta)\bigg]_{\phi=0}^{\pi}\,d\theta =\frac{4}{3}\int_0^{2\pi}\sin^2(\theta)\,d\theta\\[2.5mm] &=\frac{2}{3}\int_0^{2\pi}\left(1-\cos(2\theta)\right)\,d\theta=\frac{2}{3}\bigg[\theta-\frac{1}{2}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}=\frac{4}{3}\pi, \end{align*}

which is much more tedious.

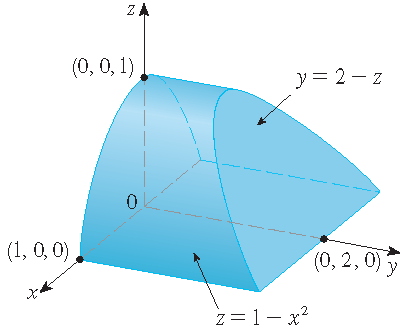Stewart §16.9, Example 2
Evaluate \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}\), where

\[\mathbf{F}(x,y,z)=xy\,\mathbf{i}+\left(y^2+e^{xz^2}\right)\,\mathbf{j}+\sin(xy)\,\mathbf{k}\]

and \(S\) is the boundary surface of the region \(E\) bounded by the parabolic cylinder \(z=1-x^2\) and the planes \(z=0\), \(y=0\) and \(y+z=2\).

Solution: It would be extremely difficult to evaluate the given surface integral directly. However, we have

\[\textrm{div}\,\mathbf{F}=\frac{\partial}{\partial x}(xy)+\frac{\partial}{\partial y}\left(y^2+e^{xz^2}\right)+\frac{\partial}{\partial z}\sin(xy) =y+2y+0=3y.\]

Now application of Gauss's divergence theorem leads to \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV\), where

\[E=\{(x,y,z)\,|\,-1\leq x\leq 1,\;0\leq z\leq 1-x^2,\;0\leq y\leq 2-z\}.\]

Hence we have

\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\iiint\limits_E\textrm{div}\,\mathbf{F}\,dV=\iiint\limits_E3y\,dS =3\int_{-1}^1\int_0^{1-x^2}\int_0^{2-z}y\,dy\,dz\,dx=\frac{3}{2}\int_{-1}^1\int_0^{1-x^2}(2-z)^2\,dz\,dx\\[2.5mm] &=\frac{3}{2}\int_{-1}^1\bigg[-\frac{1}{3}(2-z)^3\bigg]_{z=0}^{1-x^2}\,dx=\frac{1}{2}\int_{-1}^1\left(8-(1+x^2)^3\right)\,dx =\frac{1}{2}\int_{-1}^1\left(7-3x^2-3x^4-x^6\right)\,dx\\[2.5mm] &=\int_0^1\left(7-3x^2-3x^4-x^6\right)\,dx=\bigg[7x-x^3-\frac{3}{5}x^5-\frac{1}{7}x^7\bigg]_{x=0}^1 =7-1-\frac{3}{5}-\frac{1}{7}=\frac{210-21-5}{35}=\frac{184}{35}. \end{align*}

---

Last modified on October 20, 2021