Calculus – Vector calculus – The fundamental theorem for line integrals

Theorem: Let \(\mathcal{C}\) be a smooth curve given by the vector function \(\mathbf{r}(t)\) with \(a\leq t\leq b\). Let \(f\) be a differentiable function of two or three variables whose gradient vector \(\nabla f\) is continuous on \(\mathcal{C}\). Then

\[\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r}=f(\mathbf{r}(b))-f(\mathbf{r}(a)).\]

Proof: Note that we have

\[\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r}=\int_a^b\nabla f(\mathbf{r}(t))\cdot \mathbf{r}'(t)\,dt =\int_a^b\left(\frac{\partial f}{\partial x}\cdot\frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot\frac{dy}{dt}+\frac{\partial f}{\partial z}\cdot\frac{dz}{dt}\right)\,dt =\int_a^b\frac{d}{dt}f(\mathbf{r}(t))\,dt=f(\mathbf{r}(b))-f(\mathbf{r}(a)).\]

Independence of path

Definition: If \(\mathbf{F}\) is a continuous vector field with domain \(D\), then the line integral \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is called independent of path if

\[\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\]

for any two paths \(\mathcal{C}_1\) and \(\mathcal{C}_2\) in \(D\) that have the same initial point and the same terminal point.

Definition: A curve \(\mathcal{C}\) with parametrization \(\mathbf{r}(t)\) and \(a\leq t\leq b\) is called closed if its terminal point coincides with its initial point, that is, if \(\mathbf{r}(b)=\mathbf{r}(a)\).

Theorem: The line integral \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is independent of path in \(D\) if and only if \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) for every closed path \(\mathcal{C}\) in \(D\).

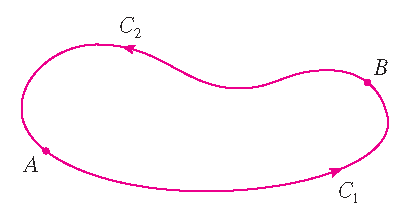Proof: If \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is independent of path in \(D\) and \(\mathcal{C}\) is any closed path in \(D\), we can choose any two points \(A\) and \(B\) on \(\mathcal{C}\) and regard the curve \(\mathcal{C}\) as being composed of the path \(\mathcal{C}_1\) from \(A\) to \(B\) followed by the path \(\mathcal{C}_2\) from \(B\) to \(A\). Then:

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} +\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} -\int\limits_{-\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=0\]

since \(\mathcal{C}_1\) and \(-\mathcal{C}_2\) have the same initial and terminal points.

Conversely, if \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) for every closed path \(\mathcal{C}\) in \(D\), then independence of path is demonstrated as follows. Take any two paths \(\mathcal{C}_1\) and \(\mathcal{C}_2\) from \(A\) to \(B\) in \(D\) and define \(\mathcal{C}\) to be the curve consisting of \(\mathcal{C}_1\) followed by \(-\mathcal{C}_2\). Then

\[0=\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} +\int\limits_{-\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} -\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\]

and so \(\displaystyle\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\), which shows that \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is independent of path in \(D\).

Definition: A region \(D\) is called open if for every point \(P\) in \(D\) there is a disk with center \(P\) (and positive radius) that lies entirely in \(D\).

Note: So \(D\) doesn't contain any of its boundary points.

Definition: A region \(D\) is called connected if any two points in \(D\) can be joined by a path that lies in \(D\).

Theorem: Suppose \(\mathbf{F}\) is a vector field that is continuous on an open connected region \(D\). If \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is independent of path in \(D\), then \(\mathbf{F}\) is a conservative vector field on \(D\), that is, there exists a (potential) function \(f\) such that \(\mathbf{F}=\nabla f\).

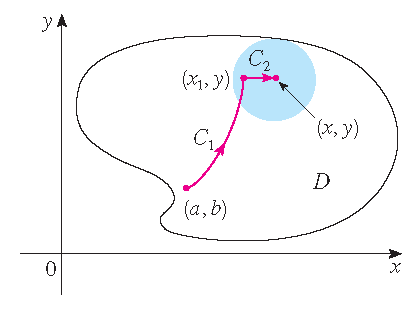Proof: Let \((a,b)\) be a fixed point in \(D\). We construct the desired potential function \(f\) by defining \(f(x,y)=\displaystyle\int_{(a,b)}^{(x,y)}\mathbf{F}\cdot d\mathbf{r}\) for any point \((x,y)\) in \(D\). Since \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is independent of path, is doesn't matter which path \(\mathcal{C}\) from \((a,b)\) to \((x,y)\) is used to evaluate \(f(x,y)\). Since \(D\) is open, there exists a disk contained in \(D\) with center \((x,y)\). Choose any point \((x_1,y)\) in the disk with \(x_1 < x\) and let \(\mathcal{C}\) consist of any path \(\mathcal{C}_1\) from \((a,b)\) to \((x_1,y)\) followed by the horizontal line segment \(\mathcal{C}_2\) from \((x_1,y)\) to \((x,y)\). Then

\[f(x,y)=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}+\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r} =\int_{(a,b)}^{(x_1,y)}\mathbf{F}\cdot d\mathbf{r}+\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}.\]

Note that the first integral does not depend on \(x\), so: \(\displaystyle\frac{\partial}{\partial x}f(x,y)=0+\frac{\partial}{\partial x}\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\). Let \(\mathbf{F}=\langle P,Q \rangle\), then \(\displaystyle\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r} =\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy\). On \(\mathcal{C}_2\) \(y\) is constant, so \(dy=0\). Using \(t\) as the parameter, where \(x_1\leq t\leq x\), we have

\[\frac{\partial}{\partial x}f(x,y)=\frac{\partial}{\partial x}\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy =\frac{\partial}{\partial x}\int_{x_1}^xP(t,y)\,dt=P(x,y).\]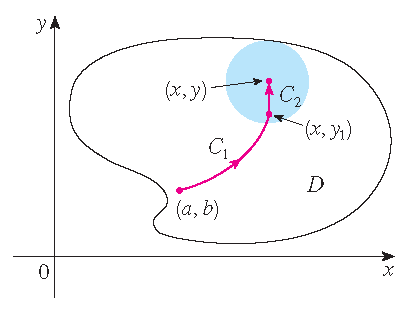

Similarly, we can choose any point \((x,y_1)\) in the disk with \(y_1 < y\) and let \(\mathcal{C}\) consist of any path \(\mathcal{C}_1\) from \((a,b)\) to \((x,y_1)\) followed by the vertical line segment \(\mathcal{C}_2\) from \((x,y_1)\) to \((x,y)\). Then

\[\frac{\partial}{\partial y}f(x,y)=\frac{\partial}{\partial y}\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy =\frac{\partial}{\partial y}\int_{y_1}^yQ(x,t)\,dt=Q(x,y).\]

Hence we have: \(\mathbf{F}=\langle P,Q \rangle =\displaystyle\frac{\partial f}{\partial x}\,\mathbf{i}+\frac{\partial f}{\partial y}\,\mathbf{j}=\nabla f\), which implies that \(\mathbf{F}\) is conservative.

Conservative vector fields

Theorem: If \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) is a conservative vector field, where \(P\) and \(Q\) have continuous first-order partial derivatives on a domain \(D\), then throughout \(D\) we have \[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.\]

Proof: Since \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) is a conservative vector field, there is a (potential) function \(f\) such that \(\mathbf{F}=\nabla f\) which implies that \(P=\displaystyle\frac{\partial f}{\partial x}\) and \(Q=\displaystyle\frac{\partial f}{\partial y}\). Therefore, by Clairaut's theorem, we have

\[\frac{\partial P}{\partial y}=\frac{\partial^2f}{\partial y\,\partial x}=\frac{\partial^2f}{\partial x\,\partial y}=\frac{\partial Q}{\partial x}.\]

Stewart §16.3, Example 3 and Example 4
Evaluate \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), where \(\mathbf{F}(x,y)=(3+2xy)\,\mathbf{i}+(x^2-3y^2)\,\mathbf{j}\) and \(\mathcal{C}\) is the curve given by \(\mathbf{r}(t)=e^t\sin(t)\,\mathbf{i}+e^t\cos(t)\,\mathbf{j}\) with \(0\leq t\leq\pi\).

Solution: Note that \(\mathbf{F}=\langle P,Q \rangle\) with \(P(x,y)=3+2xy\) and \(Q(x,y)=x^2-3y^2\). Then: \(\displaystyle\frac{\partial P}{\partial y}=2x=\frac{\partial Q}{\partial x}\), which implies that \(\mathbf{F}\) is conservative. Hence: there exists a (potential) function \(f\) such that \(\mathbf{F}=\nabla f\):

\[f_x(x,y)=3+2xy\quad\Longrightarrow\quad f(x,y)=3x+x^2y+g(y),\] which implies that \(f_y(x,y)=x^2+g'(y)\) which equals \(Q(x,y)=x^2-3y^2\) if \(g'(y)=-3y^2\). Hence: \(g(y)=-y^3+K\) for some constant \(K\). So \(f(x,y)=3x+x^2y-y^3+K\) is a potential function for any constant \(K\).

Since \(\mathbf{r}(0)=(0,1)\) and \(\mathbf{r}(\pi)=(0,-e^{\pi})\), we conclude that

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r} =f(\mathbf{r}(\pi))-f(\mathbf{r}(0))=f(0,-e^{\pi})-f(0,1)=e^{3\pi}-(-1)=e^{3\pi}+1.\]

Definition: A curve \(\mathcal{C}\) is called simple if it doesn't intersect itself anywhere.

simple, not closed	not simple, not closed	simple, closed	not simple, closed

Definition: A region \(D\) is called simply-connected if it is connected such that every simple closed curve in \(D\) encloses only points that are in \(D\).

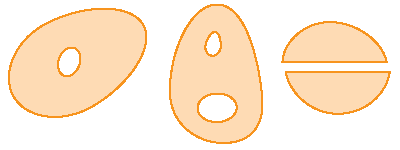simply connected	not simply connected

Theorem: Let \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) be a vector field on an open simply-connected region \(D\). Suppose that \(P\) and \(Q\) have continuous first-order partial derivatives and

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{throughout}\quad D.\]

Then \(\mathbf{F}\) is conservative.

Proof: This is a consequence of Green's theorem and will be proved later.

Stewart §16.3, Exercise 35
Let \(\mathbf{F}(x,y)=\displaystyle-\frac{y}{x^2+y^2}\,\mathbf{i}+\frac{x}{x^2+y^2}\,\mathbf{j}\). Show that \(\displaystyle\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\) and show that \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is not independence of path.

Solution: Let \(P(x,y)=-\displaystyle\frac{y}{x^2+y^2}\) and \(Q(x,y)=\displaystyle\frac{x}{x^2+y^2}\), then:

\[\frac{\partial P}{\partial y}=\frac{-(x^2+y^2)+2y^2}{(x^2+y^2)^2}=\frac{y^2-x^2}{(x^2+y^2)^2}\quad\textrm{and}\quad \frac{\partial Q}{\partial x}=\frac{x^2+y^2-2-x^2}{(x^2+y^2)^2}=\frac{y^2-x^2}{(x^2+y^2)^2}.\]

Note that this holds on the domain \(\mathbb{R}^2\setminus\{(0,0)\}\), which is not simply-connected because of the perforation. This implies that the theorem cannot be applied.

Let \(\mathcal{C}_1\) be the upper half of the unit circle \(x^2+y^2=1\) from \((1,0)\) to \((-1,0)\) with parametrization \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) and \(0\leq t\leq\pi\). Then we have

\[\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int_0^{\pi}\langle -\sin(t),\cos(t) \rangle\cdot\langle -\sin(t),\cos(t) \rangle\,dt =\int_0^{\pi}(\sin^2(t)+\cos^2(t))\,dt=\int_0^{\pi}dt=\pi.\]

However, let \(\mathcal{C}_2\) be the lower half of the unit circle \(x^2+y^2=1\) from \((1,0)\) to \((-1,0)\) with parametrization \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+-\sin(t)\,\mathbf{j}\) and \(0\leq t\leq\pi\). Then we have

\[\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int_0^{\pi}\langle \sin(t),\cos(t) \rangle\cdot\langle -\sin(t),-\cos(t) \rangle\,dt =\int_0^{\pi}(-\sin^2(t)-\cos^2(t))\,dt=-\int_0^{\pi}dt=-\pi.\]

Hence: \(\displaystyle\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}\neq\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\), which implies that \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is not independece of path.

---

Last modified on October 11, 2021