Calculus – Vector calculus – Line integrals

The line integral of a scalar function

Definition: If \(f\) is a (scalar) function defined on a smooth curve \(\mathcal{C}\) in \(\mathbb{R}^2\) or \(\mathbb{R}^3\) defined by the parametrization \(\mathbf{r}(t)\) with \(a\leq t\leq b\), then

\[\int\limits_{\mathcal{C}}f(x,y)\,ds=\int_a^bf(\mathbf{r}(t))|\mathbf{r}'(t)|\,dt\quad\textrm{or}\quad \int\limits_{\mathcal{C}}f(x,y,z)\,ds=\int_a^bf(\mathbf{r}(t))|\mathbf{r}'(t)|\,dt\]

is the line integral of \(f\) along the curve \(\mathcal{C}\).

Remark: If \(f\) is the constant \(1\), then we obtain the arc length of the curve: \(L=\displaystyle\int\limits_{\mathcal{C}}ds=\int_a^b|\mathbf{r}'(t)|\,dt\).

Stewart §16.2, Example 1
Evaluate \(\displaystyle\int\limits_{\mathcal{C}}(2+x^2y)\,ds\), where \(\mathcal{C}\) is the upper half of the unit circle \(x^2+y^2=1\).

Solution: Note that \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) with \(0\leq t\leq \pi\) is a (possible) parametrization of the curve \(\mathcal{C}\). Then we have \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) and therefore \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2}=1\). Hence:

\[\int\limits_{\mathcal{C}}(2+x^2y)\,ds=\int_0^{\pi}(2+\cos^2(t)\sin(t))\cdot1\,dt=\bigg[2t-\frac{1}{3}\cos^3(t)\bigg]_{t=0}^{\pi} =2\pi+\frac{2}{3}.\]

Stewart §16.2, Example 5
Evaluate \(\displaystyle\int\limits_{\mathcal{C}}y\,\sin(z)\,ds\), where \(\mathcal{C}\) is the circular helix given by \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+t\,\mathbf{k}\) with \(0\leq t\leq 2\pi\).

Solution: Note that \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}+1\,\mathbf{k}\) and therefore \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{2}\). Hence:

\[\int\limits_{\mathcal{C}}y\,\sin(z)\,ds=\int_0^{2\pi}\sin(t)\,\sin(t)\,\sqrt{2}\,dt=\sqrt{2}\int_0^{2\pi}\sin^2(t)\,dt =\frac{1}{2}\sqrt{2}\int_0^{2\pi}(1-\cos(2t))\,dt=\frac{1}{2}\sqrt{2}\bigg[t-\frac{1}{2}\sin(2t)\bigg]_{y=0}^{2\pi}=\pi\sqrt{2}.\]

Application: physical interpretation

Suppose that \(\rho(x,y)\geq 0\) is a mass density function defined at the points \((x,y)\) of a thin wire shaped like a curve \(\mathcal{C}\). Then

\[m=\int\limits_{\mathcal{C}}\rho(x,y)\,ds\]

denotes the (total) mass of the wire. Furthermore, the center of mass \((\overline{x},\overline{y})\) is given by

\[\overline{x}=\frac{1}{m}\int\limits_{\mathcal{C}}x\,\rho(x,y)\,ds\quad\textrm{and}\quad\overline{y}=\frac{1}{m}\int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds.\]

Stewart §16.2, Example 3
A wire takes the shape of the semicircle \(x^2+y^2=1\) with \(y\geq 0\). Find the center of mass of the wire if the mass density is \(\rho(x,y)=k(1-y)\) with \(k\) a constant.

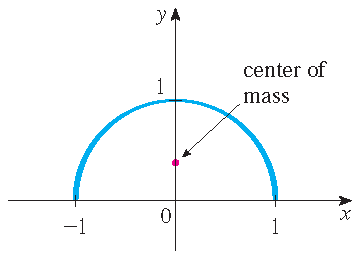
Solution: Note that \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) with \(0\leq t\leq \pi\) is a (possible) parametrization of the curve \(\mathcal{C}\). Then we have

\[m=\int\limits_{\mathcal{C}}\rho(x,y)\,ds=\int\limits_{\mathcal{C}}k(1-y)\,ds=k\int_0^{\pi}(1-\sin(t))\cdot1\,dt =k\bigg[t+\cos(t)\bigg]_{y=0}^{\pi}=k(\pi-2).\]

The symmetry of both the wire and the mass density function implies that \(\overline{x}=0\). Furthermore, we have

\begin{align*} \int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds&=\int\limits_{\mathcal{C}}k\,y(1-y)\,ds=k\int_0^{\pi}\sin(t)(1-\sin(t))\cdot1\,dt =k\int_0^{\pi}\left(\sin(t)-\frac{1}{2}+\frac{1}{2}\cos(2t)\right)\,dt\\[2.5mm] &=k\bigg[-\cos(t)-\frac{1}{2}t+\frac{1}{4}\sin(2t)\bigg]_{y=0}^{\pi}=k\left(2-\tfrac{1}{2}\pi\right). \end{align*}

This implies that \(\overline{y}=\displaystyle\frac{1}{m}\int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds=\frac{4-\pi}{2(\pi-2)}\approx0.376\).

Remark: Similarly (of course) for (space) curves in \(\mathbb{R}^3\).

The line integral of a vector field

Definition: Let \(\mathbf{F}\) be a continuous vector field defined on a smooth curve given by a vector function \(\mathbf{r}(t)\) with \(a\leq t\leq b\). Then

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int_a^b\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt\]

is the line integral of \(\mathbf{F}\) along the curve \(\mathcal{C}\).

This line integral defines the work done by the force field \(\mathbf{F}\) in moving a particle along the curve \(\mathcal{C}\) from \(\mathbf{r}(a)\) to \(\mathbf{r}(b)\).

Stewart §16.2, Example 7
Find the work done by the force field \(\mathbf{F}(x,y)=x^2\,\mathbf{i}-xy\,\mathbf{j}\) in moving a particle along the quarter-circle \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j},\; 0\leq t\leq\frac{1}{2}\pi\).

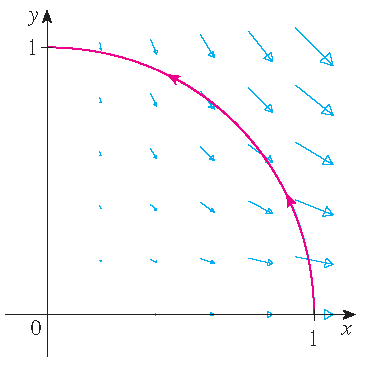
Solution: Note that \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) and therefore

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^{\frac{1}{2}\pi}\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^{\frac{1}{2}\pi}\langle \cos^2(t),-\cos(t)\sin(t) \rangle\cdot\langle -\sin(t),\cos(t) \rangle\,dt\\[2.5mm] &=\int_0^{\frac{1}{2}\pi}\left(-2\cos^2(t)\sin(t)\right)\,dt=\frac{2}{3}\cos^3(t)\bigg|_0^{\frac{1}{2}\pi}=-\frac{2}{3}. \end{align*}

Remark: The sign of a line integral of a vector field depends on the orientation of the curve: \(\displaystyle\int\limits_{\mathcal{-C}}\mathbf{F}\cdot d\mathbf{r}=-\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\).

Stewart §16.2, Example 8
Evaluate \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), where \(\mathbf{F}(x,y,z)=xy\,\mathbf{i}+yz\,\mathbf{j}+xz\,\mathbf{k}\) and \(\mathcal{C}\) is the twisted cubic given by \(\mathbf{r}(t)=t\,\mathbf{i}+t^2\,\mathbf{j}+t^3\,\mathbf{k}\) with \(0\leq t\leq 1\).

Solution: Note that \(\mathbf{r}'(t)=1\,\mathbf{i}+2t\,\mathbf{j}+3t^2\,\mathbf{k}\) and therefore

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^1\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^1\langle t^3,t^5,t^4 \rangle\cdot\langle 1,2t,3t^2 \rangle\,dt=\int_0^1\left(t^3+2t^6+3t^6\right)\,dt\\[2.5mm] &=\bigg[\frac{1}{4}t^4+\frac{5}{7}t^7\bigg]_{t=0}^1=\frac{1}{4}+\frac{5}{7}=\frac{7+20}{28}=\frac{27}{28}. \end{align*}

Notation: If \(\mathbf{F}=\langle P,Q \rangle\) in \(\mathbb{R}^2\), then: \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}P\,dx+Q\,dy\). If \(\mathbf{F}=\langle P,Q,R \rangle\) in \(\mathbb{R}^3\), then: \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}P\,dx+Q\,dy+R\,dz\).

---

Last modified on October 9, 2021