Calculus – Vector calculus – The area of a surface
Parametric surfaces
We consider a parametric surface \(S\) given by:
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D.\]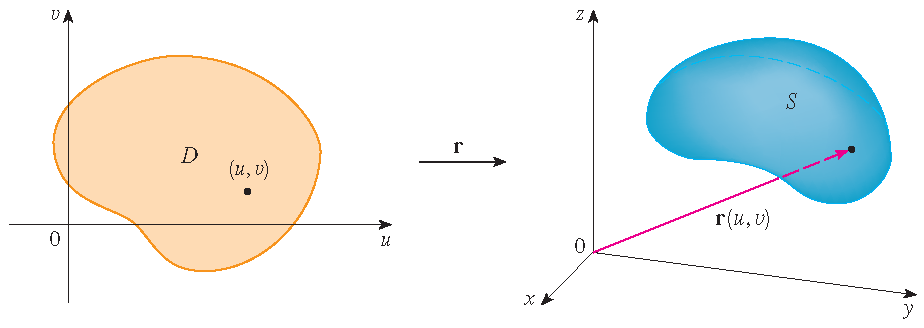
This is called a parametrization of the surface \(S\) with \(D\) the domain of the parametrization.
Note: Usually we assume that \(\mathbf{r}(u,v)\) is one-to-one on the interior of the parameter domain \(D\).
Stewart §16.6, Example 1
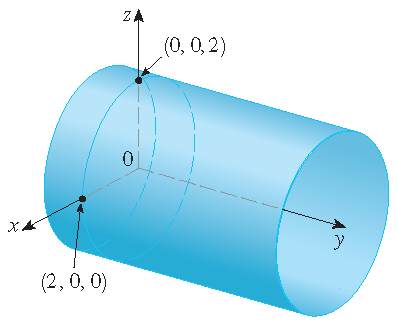
Identify and sketch the surface with parametrization \(\mathbf{r}(u,v)=2\cos(u)\,\mathbf{i}+v\,\mathbf{j}+2\sin(u)\,\mathbf{k}\).
Solution: Note that \(x=2\cos(u)\) and \(z=2\sin(u)\) which implies that \(x^2+z^2=4\). This leads to the circular cylinder with radius \(2\) whose axis is the \(y\)-axis:
Grid curves
If a parametric surface \(S\) is given by a vector function \(\mathbf{r}(u,v)\), then there are two useful families of curves that lie on \(S\), one family with \(u\) constant and the other with \(v\) constant. These families correspond to vertical and horizontal lines in the \(uv\)-plane.
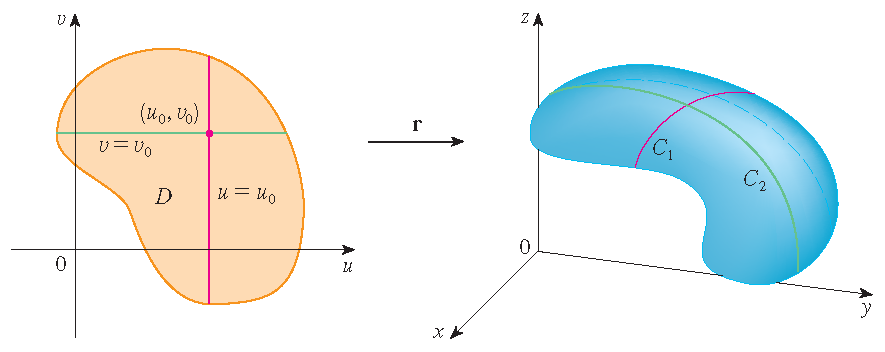
If we keep \(u\) constant by putting \(u=u_0\), then \(\mathbf{r}(u_0,v)\) becomes a vector function of the single parameter \(v\) and defines a curve \(\mathcal{C}_1\) lying on \(S\). Similarly, if we keep \(v\) constant by putting \(v=v_0\), we get a curve \(\mathcal{C}_2\) given by \(\mathbf{r}(u,v_0)\) that lies on \(S\). These curves are called grid curves.
Stewart §16.6, Example 4
Find a parametric representation of the sphere \(x^2+y^2+z^2=a^2\) with \(a > 0\).
Solution: The sphere has a simple representation \(\rho=a\) in spherical coordinates. So, we might use the angles \(\theta\) and \(\phi\) in spherical coordinates as the parameters:
\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k}, \quad 0\leq\phi\leq \pi,\quad 0\leq\theta\leq 2\pi.\]Stewart §16.6, Example 5
Find a parametric representation or parametrization for the cylinder \(x^2+y^2=4\) and \(0\leq z\leq 1\).
Solution: The cylinder has a simple representation \(r=2\) in cylindrical coordinates. So, if we choose as parameters \(\theta\) and \(z\) in cylindrical coordinates, we obtain:
\[\mathbf{r}(\theta,z)=2\cos(\theta)\,\mathbf{i}+2\sin(\theta)\,\mathbf{j}+z\,\mathbf{k},\quad 0\leq\theta\leq 2\pi,\quad 0\leq z\leq 1.\]Parametric representations or parametrizations of surfaces are not unique. In the next two examples we see two different ways to parametrize a surface.
Stewart §16.6, Example 6
Find a vector function that represents the elliptic paraboloid \(z=x^2+2y^2\).
Solution: Note that the surface is the graph of the function \(f(x,y)=x^2+2y^2\) of two variables \(x\) and \(y\). So if we choose \(x\) and \(y\) as parameters, we obtain
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x^2+2y^2)\,\mathbf{k}.\]Another parametrization might be
\[\mathbf{r}(r,\theta)=\sqrt{2}\,r\cos(\theta)\,\mathbf{i}+r\sin(\theta)\,\mathbf{j}+2r^2\,\mathbf{k},\quad r\geq0,\quad 0\leq\theta\leq 2\pi.\]Stewart §16.6, Example 7
Find a parametric representation for the surface \(z=2\sqrt{x^2+y^2}\), that is, the top half of the cone \(z^2=4x^2+4y^2\).
Solution: Again the surface can be seen as the graph of a function of two variables:
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+2\sqrt{x^2+y^2}\,\mathbf{k}.\]Another parametrizations is based on the polar coordinates \(r\) and \(\theta\):
\[\mathbf{r}(r,\theta)=r\cos(\theta)\,\mathbf{i}+r\sin(\theta)\,\mathbf{j}+2r\,\mathbf{k},\quad r\geq0,\quad 0\leq\theta\leq 2\pi.\]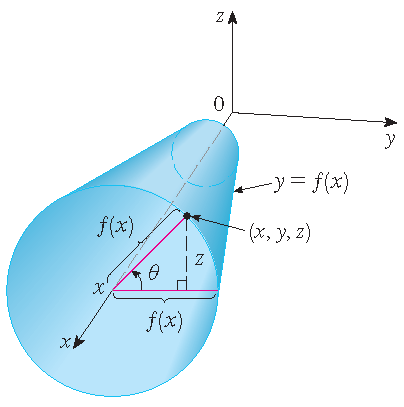
Surfaces of revolution
Consider the surface \(S\) obtained by rotating the curve \(y=f(x)\) with \(a\leq x\leq b\) about the \(x\)-axis, where \(f(x)\geq 0\). Let \(\theta\) be the angle of rotation, then
\[S:\;\mathbf{r}(x,\theta)=x\,\mathbf{i}+f(x)\cos(\theta)\,\mathbf{j}+f(x)\sin(\theta)\,\mathbf{k},\quad a\leq x\leq b,\quad 0\leq\theta\leq2\pi.\]See the picture on the right.
Stewart §16.6, Example 8
Find a parametrization for the surface generated by rotating the curve \(y=\sin(x)\) with \(0\leq x\leq 2\pi\) about the \(x\)-axis.
Solution: We have
\[\mathbf{r}(x,\theta)=x\,\mathbf{i}+\sin(x)\cos(\theta)\,\mathbf{j}+\sin(x)\sin(\theta)\,\mathbf{k},\quad 0\leq x\leq 2\pi,\quad 0\leq\theta\leq 2\pi.\]The surface of revolution looks like this:

Tangent planes
We want to find the tangent plane to a parametric surface \(S\) traced out by a vector function
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k}\]at a point \(P_0\) with position vector \(\mathbf{r}(u_0,v_0)\). If we keep \(u\) constant by putting \(u=u_0\), then \(\mathbf{r}(u_0,v)\) becomes a vector function of the single variable \(v\) and defines a grid curve \(\mathcal{C}_1\) lying on \(S\). The tangent vector to \(\mathcal{C}_1\) at \(P_0\) is obtained by taking the partial derivative of \(\mathbf{r}\) with respect to \(v\):
\[\mathbf{r}_v=x_v(u_0,v_0)\,\mathbf{i}+y_v(u_0,v_0)\,\mathbf{j}+z_v(u_0,v_0)\,\mathbf{k}.\]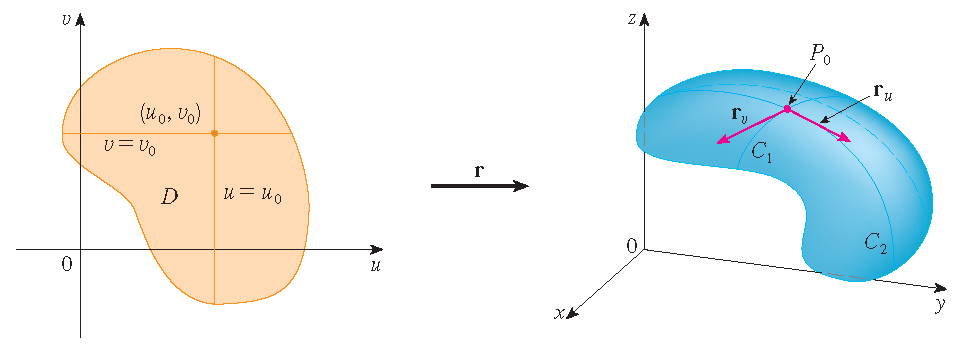
Similarly, if we keep \(v\) constant by putting \(v=v_0\), we get a grid curve \(\mathcal{C}_2\) given by \(\mathbf{r}(u,v_0)\) that lies on \(S\) and its tangent vector at \(P_0\) is
\[\mathbf{r}_u=x_u(u_0,v_0)\,\mathbf{i}+y_u(u_0,v_0)\,\mathbf{j}+z_u(u_0,v_0)\,\mathbf{k}.\]If \(\mathbf{r}_u\times\mathbf{r}_v\) is not \(\mathbf{0}\), then the surface \(S\) is called smooth. For a smooth surface, the tangent plane is the plane that contains the tangent vectors \(\mathbf{r}_u\) and \(\mathbf{r}_v\) and the vector \(\mathbf{r}_u\times\mathbf{r}_v\) is a normal vector to the tangent plane.
Surface area
We want to find the area of a parametric surface. For simplicity we start by considering a surface whose parameter domain \(D\) is a rectangle and divide it into subrectangles \(R_{ij}\). We choose \((u_i^*,v_j^*)\) to be the lower left corner of \(R_{ij}\):
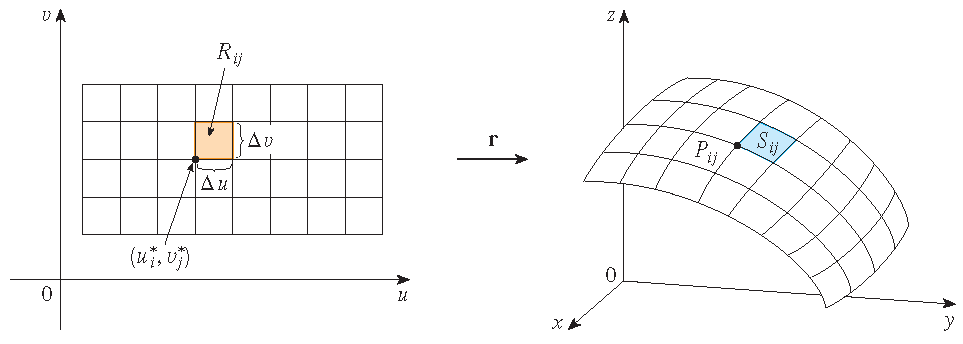
The part \(S_{ij}\) of the surface \(S\) that corresponds to \(R_{ij}\) is called a patch and has the point \(P_{ij}\) with position vector \(\mathbf{r}(u_i^*,v_j^*)\) as one of its corners. Let
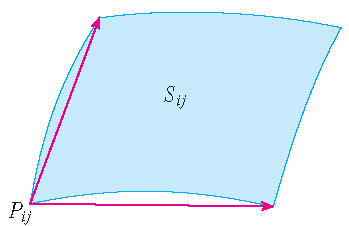
\[\mathbf{r}_u^*=\mathbf{r}_u(u_i^*,v_j^*)\quad\textrm{and}\quad\mathbf{r}_v^*=\mathbf{r}_v(u_i^*,v_j^*)\]be the tangent vectors at \(P_{ij}\).
 |
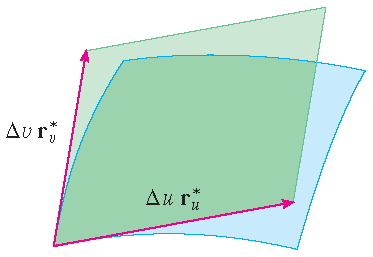 |
The picture shows that how the two edges of the patch that meet at \(P_{ij}\) can be approximated by vectors. These vectors, in turn, can be approximated by the vectors \(\Delta u\,\mathbf{R}_u^*\) and \(\Delta v\,\mathbf{r}_v^*\) because partial derivatives can be approximated by difference quotients. So we approximate \(S_{ij}\) by the parallelogram determined by the vectors \(\Delta u\,\mathbf{r}_u^*\) and \(\Delta v\,\mathbf{r}_v^*\). This parallelogram is shown in the picture and lies in the tangent plane to \(S\) at \(P_{ij}\). The area of this parallelogram is
\[\left|\left(\Delta u\,\mathbf{r}_u^*\right)\times\left(\Delta v\,\mathbf{r}_v^*\right)\right| =\left|\mathbf{r}_u^*\times\mathbf{r}_v^*\right|\,\Delta u\,\Delta v.\]Therefore, an approximation of the area of \(S\) is
\[\sum_{i=1}^m\sum_{j=1}^n\left|\mathbf{r}_u^*\times\mathbf{r}_v^*\right|\,\Delta u\,\Delta v.\]This approximation gets better if we increase the number of subrectangles and we recognize the double sum as a Riemann sum for a double integral. This motivates the following definition.
Definition: If a smooth parametric surface \(S\) is given by
\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D\]and \(S\) is covered just once as \((u,v)\) ranges throughout the parameter domain \(D\), then the surface area of \(S\) is
\[\textrm{area}(S)=\iint\limits_D\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA,\]where \(\displaystyle\mathbf{r}_u=\frac{\partial x}{\partial u}\,\mathbf{i}+\frac{\partial y}{\partial u}\,\mathbf{j}+\frac{\partial z}{\partial u}\,\mathbf{k}\) and \(\displaystyle\mathbf{r}_v=\frac{\partial x}{\partial v}\,\mathbf{i}+\frac{\partial y}{\partial v}\,\mathbf{j}+\frac{\partial z}{\partial v}\,\mathbf{k}\).
Stewart §16.6, Example 10
Find the surface area of a sphere with radius \(a > 0\).
Solution: A parametrization of the sphere is
\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq \pi,\quad 0\leq\theta\leq 2\pi.\]The cross product of the tangent vectors
\[\mathbf{r}_{\phi}=a\,\cos(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\cos(\phi)\,\sin(\theta)\,\mathbf{j}-a\,\sin(\phi)\,\mathbf{k}\quad\textrm{and}\quad \mathbf{r}_{\theta}=-a\,\sin(\phi)\,\sin(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\cos(\theta)\,\mathbf{j}+0\,\mathbf{k}\]is
\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=a^2\,\sin^2(\phi)\,\cos(\theta)\,\mathbf{i}+a^2\,\sin^2(\phi)\,\sin(\theta)\,\mathbf{j} +a^2\,\sin(\phi)\,\cos(\phi)\,\mathbf{k}=a\,\sin(\phi)\cdot\mathbf{r}(\phi,\theta).\]Hence we have
\[\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|=a\,|\sin(\phi)|\cdot a=a^2\,\sin(\phi),\]since \(\sin(\phi)\geq0\) for \(0\leq\phi\leq\pi\). Therefore, using the definition, the area of the sphere is
\[\iint\limits_D\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA=\int_0^{2\pi}\int_0^{\pi}a^2\,\sin(\phi)\,d\phi\,d\theta =a^2\int_0^{2\pi}\,d\theta\,\int_0^{\pi}\sin(\phi)\,d\phi=a^2\cdot2\pi\cdot2=4]pi a^2.\]Stewart §16.6, Example 11
Find the area of the part of the paraboloid \(z=x^2+y^2\) that lies under the plane \(z=9\).
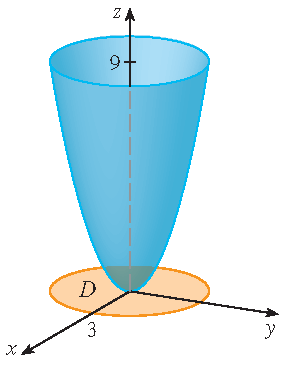
Solution: The plane \(z=9\) intersects the paraboloid in the circle \(x^2+y^2=9\). Therefore the given surface lies above the disk \(D\) with center the origin and radius \(3\). A parametrization of the surface is
\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x^2+y^2)\,\mathbf{k},\quad (x,y)\in D=\{(x,y)\,|\,x^2+y^2\leq 9\}.\]Hence the surface area equals \(\displaystyle\iint\limits_D\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA\) with \(\mathbf{r}_x=\mathbf{i}+2x\,\mathbf{k}\) and \(\mathbf{r}_y=\mathbf{j}+2y\,\mathbf{k}\). Now we have
\[\left|\mathbf{r}_x\times\mathbf{r}_y\right|=\left|-2x\,\mathbf{i}-2y\,\mathbf{j}+\mathbf{k}\right|=\sqrt{(-2x)^2+(-2y)^2+1} =\sqrt{4x^2+4y^2+1}.\]Using polar coordinates we find that the surface area equals
\begin{align*} \iint\limits_D\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA&=\iint\limits_D\sqrt{4x^2+4y^2+1}\,dA =\int_0^{2\pi}\int_0^3\sqrt{4r^2+1}\,r\,dr\,d\theta=\int_0^{2\pi}\,d\theta\,\int_0^3r\sqrt{4r^2+1}\,dr\\[2.5mm] &=2\pi\bigg[\frac{1}{12}(4r^2+1)^{3/2}\bigg]_{r=0}^3=\frac{1}{6}\pi\left(37\sqrt{37}-1\right). \end{align*}The area of a torus
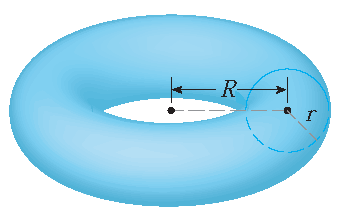 A parametrization of a torus that is obtained by rotating a vertical circle with radius \(r\) around the \(z\)-axis with the center of the
circle at a distance \(R\) from the \(z\)-axis with \(0 < r < R\) is
A parametrization of a torus that is obtained by rotating a vertical circle with radius \(r\) around the \(z\)-axis with the center of the
circle at a distance \(R\) from the \(z\)-axis with \(0 < r < R\) is
with \(0\leq\theta\leq2\pi\) and \(0\leq\phi\leq2\pi\).
Note that the volume equals \(2\pi\,R\cdot\pi\,r^2=2\pi^2\,r^2\,R\) being the product of the circumference of a circle with radius \(R\) and the area of a circle with radius \(r\).
In order to find the surface area of the torus we obtain
\begin{align*} \mathbf{r}_{\theta}\times\mathbf{r}_{\phi}&=\langle-(R+r\,\cos(\phi))\sin(\theta),(R+r\,\cos(\phi)\cos(\theta),0\rangle\times \langle -r\,\sin(\phi)\,\cos(\theta),-r\,\sin(\phi)\,\sin(\theta),r\,\cos(\phi)\rangle\\[2.5mm] &=\langle r\,\cos(\phi)(R+r\,\cos(\phi))\cos(\theta),r\,\cos(\phi)(R+r\,\cos(\phi))\sin(\theta), r\,\sin(\phi)(R+r\,\cos(\phi))(\cos^2(\theta)+\sin^2(\theta))\rangle\\[2.5mm] &=\langle r\,\cos(\phi)(R+r\,\cos(\phi))\cos(\theta),r\,\cos(\phi)(R+r\,\cos(\phi))\sin(\theta), r\,\sin(\phi)(R+r\,\cos(\phi))\rangle\\[2.5mm] &=r\,(R+r\,\cos(\phi))\langle \cos(\phi)\,\cos(\theta),\cos(\phi)\,\sin(\theta),\sin(\phi)\rangle \end{align*}and therefore
\[\left|\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}\right|=r\,(R+r\,\cos(\phi))\sqrt{\cos^2(\phi)\left(\cos^2(\theta)+\sin^2(\theta)\right)+\sin^2(\phi)} =r\,(R+r\,\cos(\phi))\sqrt{\cos^2(\phi)+\sin^2(\phi)}=r\,(R+r\,\cos(\phi)).\]Hence the surface area of the torus is
\begin{align*} \int_0^{2\pi}\int_0^{2\pi}\left|\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}\right|\,d\phi\,d\theta &=\int_0^{2\pi}\int_0^{2\pi}r\,(R+r\,\cos(\phi))\,d\phi\,d\theta=2\pi\,r\,\int_0^{2\pi}(R+r\,\cos(\phi))\,d\phi =2\pi\,r\,\bigg[R\phi+r\,\sin(\phi)\bigg]_{\phi=0}^{2\pi}\\[2.5mm] &=2\pi\,r\cdot2\pi\,R=4\pi^2\,r\,R, \end{align*}which equals the product of the circumference of a circle with radius \(r\) and the circumference of a circle with radius \(R\).
Last modified on October 16, 2021
 Teaching
Teaching

