Calculus – Vector calculus – The arc length of a curve

Parametrizations of a curve

A (plane) curve \(\mathcal{C}\) in \(\mathbb{R}^2\) is the set of points \((x,y)\), where

\[x=f(t)\quad\textrm{and}\quad y=g(t)\quad\textrm{with}\quad a\leq t\leq b.\]

The vector function \(\mathbf{r}(t)=f(t)\,\mathbf{i}+g(t)\,\mathbf{j}\) with \(a\leq t\leq b\) is called a parametrization of the curve \(\mathcal{C}\).

A (space) curve \(\mathcal{C}\) in \(\mathbb{R}^3\) is the set of points \((x,y,z)\), where

\[x=f(t),\quad y=g(t)\quad\textrm{and}\quad z=h(t)\quad\textrm{with}\quad a\leq t\leq b.\]

The vector function \(\mathbf{r}(t)=f(t)\,\mathbf{i}+g(t)\,\mathbf{j}+h(t)\,\mathbf{k}\) with \(a\leq t\leq b\) is called a parametrization of the curve \(\mathcal{C}\).

Example: Parametrizations of the semicircle \(x^2+y^2=1\) with \(y\geq0\) are:

1. \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) with \(0\leq t\leq\pi\);


2. \(\mathbf{r}(t)=t\,\mathbf{i}+\sqrt{1-t^2}\,\mathbf{j}\) with \(-1\leq t\leq1\);


3. \(\mathbf{r}(t)=-t\,\mathbf{i}+\sqrt{1-t^2}\,\mathbf{j}\) with \(-1\leq t\leq1\);


4. \(\mathbf{r}(t)=(1-t)\,\mathbf{i}+\sqrt{2t-t^2}\,\mathbf{j}\) with \(0\leq t\leq2\).

The arc length of a curve

Definition: Let \(\mathcal{C}\) be a curve defined by the vector function \(\mathbf{r}(t)\) with \(a\leq t\leq b\). If the curve \(\mathcal{C}\) is traversed exactly once as \(t\) increases from \(a\) to \(b\), then

\[L=\int_a^b|\mathbf{r}'(t)|\,dt\]

denotes the arc length of the curve \(\mathcal{C}\).

Examples:

1) Find the circumference of a circle with radius \(1\), that is, the arc length of the curve \(\mathcal{C}:\;\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) with \(0\leq t\leq 2\pi\).

Solution: \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) and therefore \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2}=1\). Hence:

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=\int_0^{2\pi}1\,dt=2\pi.\]

2) Find the length of the arc of the circular helix given by \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+t\,\mathbf{k}\) with \(0\leq t\leq 2\pi\).

Solution: \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}+1\,\mathbf{k}\) and therefore \(|\mathbf{r}'(t)=\sqrt{(-\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{2}\). Hence:

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=\int_0^{2\pi}\sqrt{2}\,dt=2\pi\sqrt{2}.\]

Definition: Let \(\mathcal{C}\) be a curve defined by the vector function \(\mathbf{r}(t)\) with \(a\leq t\leq b\). If \(\mathbf{r}'\) is continuous and \(\mathcal{C}\) is traversed exactly once as \(t\) increases from \(a\) to \(b\), then

\[s(t)=\int_a^t|\mathbf{r}'(u)|\,du\]

denotes the arc length function of the curve \(\mathcal{C}\).

The function \(s(t)=\displaystyle\int_a^t|\mathbf{r}'(u)|\,du\) denotes the arc length of the part of the curve \(\mathcal{C}\) between \(\mathbf{r}(a)\) and \(\mathbf{r}(t)\). Note that \(\displaystyle\frac{ds}{dt}=|\mathbf{r}'(t)|\).

Applications: we consider the arc length of a catenary, a cycloid and a cardioid.

1) The graph of a flexible chain is called a catenary and is, for instance, given by the parametrization \(\mathbf{r}(t)=t\,\mathbf{i}+\cosh(t)\,\mathbf{j}\) with \(0\leq t\leq 2\).

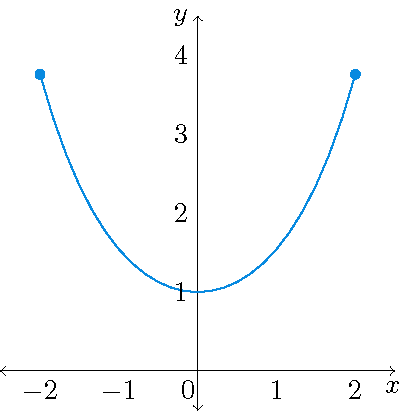
The function \(\cosh\) is called cosine hyperbolic and is defined as: \(\cosh(x)=\displaystyle\frac{e^x+e^{-x}}{2}\).

We also have the sine hyperbolic and the tangent hyperbolic defined by

\[\sinh(x)=\frac{e^x-e^{-x}}{2}\quad\textrm{and}\quad\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}.\]

See also: Stewart §3.11.

Note that we have:

\[\sinh(-x)=-\sinh(x),\quad\cosh(-x)=\cosh(x)\quad\textrm{and}\quad\tanh(-x)=-\tanh(x).\]

Furthermore we have

\[\sinh'(x)=\cosh(x),\quad\cosh'(x)=\sinh(x)\quad\textrm{and}\quad\cosh^2(x)-\sinh^2(x)=1.\]

For the arc length of the catenary we now obtain:

\begin{align*} L&=\int_{-2}^2|\mathbf{r}'(t)|\,dt=\int_{-2}^2\sqrt{1+\sinh^2(t)}\,dt=\int_{-2}^2\sqrt{\cosh^2(t)}\,dt=\int_{-2}^2\cosh(t)\,dt\\[2.5mm] &=\sinh(t)\bigg|_{-2}^2=\sinh(2)-\sinh(-2)=2\sinh(2)=e^2-e^{-2}\approx7.254. \end{align*} 2) The curve traced out by a point \(P\) on the circumference of a circle as the circle rolls along a straight line is called a cycloid (see also: Stewart §10.1 and §10.2). If the circle has radius \(r\) and rolls along the \(x\)-axis and if one position of it is the origin, then a parametrization of this cycloid is

\[\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j},\quad 0\leq t\leq 2\pi.\]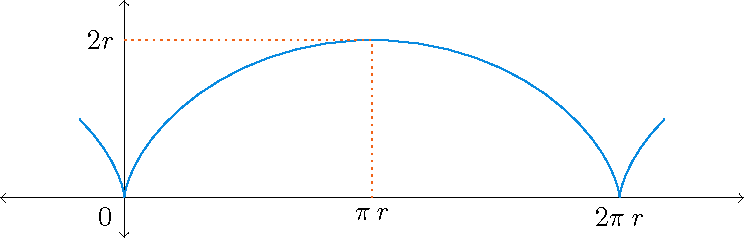

Note that

\[\mathbf{r}'(t)=r(1-\cos(t))\,\mathbf{i}+r\sin(t)\,\mathbf{j},\]

which leads to the arc length

\[L=\int_0^{2\pi}|\mathbf{r}'(t)|\,dt=r\int_0^{2\pi}\sqrt{(1-\cos(t))^2+(\sin(t))^2}\,dt=r\int_0^{2\pi}\sqrt{2-2\cos(t)}\,dt.\]

Now we use

\[\cos(2x)=\cos^2(x)-\sin^2(x)=1-2\sin^2(x)\quad\Longrightarrow\quad2\sin^2(x)=1-\cos(2x)\]

to obtain

\[L=r\int_0^{2\pi}\sqrt{2-2\cos(t)}\,dt=r\int_0^{2\pi}\sqrt{4\sin^2\left(\tfrac{t}{2}\right)}\,dt =2r\int_0^{2\pi}\left|\sin\left(\tfrac{t}{2}\right)\right|\,dt=2r\int_0^{2\pi}\sin\left(\tfrac{t}{2}\right)\,dt =2r\bigg[-2\cos\left(\tfrac{t}{2}\right)\bigg]_{t=0}^{2\pi}=8r.\]

3) Recall the cardioid in polar coordinates given by \(r=2+2\cos(\theta)\):

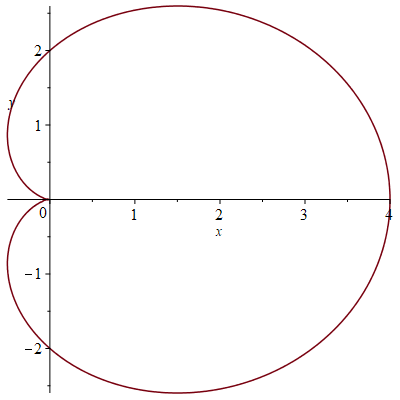
This implies that

\[\mathbf{r}(t)=(2+2\cos(t))\cos(t)\,\mathbf{i}+(2+2\cos(t))\sin(t)\,\mathbf{j},\quad 0\leq t\leq 2\pi\]

is a parametrization of this cardioid. So the arc length equals \(L=\displaystyle\int_0^{2\pi}|\mathbf{r}'(t)|\,dt\), where

\[\mathbf{r}'(t)=\langle -(2+2\cos(t))\sin(t)-2\sin(t)\cos(t),(2+2\cos(t))\cos(t)-2\sin^2(t) \rangle.\]

Hence we have

\begin{align*} \mathbf{r}'(t)|^2&=(2+2\cos(t))^2\sin^2(t)+4(2+2\cos(t))\sin^2(t)\cos(t)+4\sin^2(t)\cos^2(t)\\[2.5mm] &{}\hspace{25mm}+(2+2\cos(t))^2\cos^2(t)-4(2+2\cos(t))\sin^2(t)\cos(t)+4\sin^4(t)\\[2.5mm] &=(2+2\cos(t))^2(\sin^2(t)+\cos^2(t))+4\sin^2(t)(\cos^2(t)+\sin^2(t))\\[2.5mm] &=(2+2\cos(t))^2+4\sin^2(t)=4+8\cos(t)+4\cos^2(t)+4\sin^2(t)=8+8\cos(t) \end{align*}

and therefore

\[L=\int_0^{2\pi}\sqrt{8+8\cos(t)}\,dt=2\int_0^{\pi}\sqrt{8+8\cos(t)}\,dt=4\sqrt{2}\int_0^{\pi}\sqrt{1+\cos(t)}\,dt.\]

Note that we have for \(0 < t \leq \pi\)

\[\sqrt{1+\cos(t)}=\sqrt{1+\cos(t)}\cdot\frac{\sqrt{1-\cos(t)}}{\sqrt{1-\cos(t)}}=\frac{\sqrt{1-\cos^2(t)}}{\sqrt{1-\cos(t)}} =\frac{\sqrt{\sin^2(t)}}{\sqrt{1-\cos(t)}}=\frac{|\sin(t)|}{\sqrt{1-\cos(t)}}=\frac{\sin(t)}{\sqrt{1-\cos(t)}}.\]

Hence we have

\[L=4\sqrt{2}\int_0^{\pi}\frac{\sin(t)}{\sqrt{1-\cos(t)}}\,dt=8\sqrt{2}\,\sqrt{1-\cos(t)}\bigg|_0^{\pi}=8\sqrt{2}\cdot\sqrt{2}=16.\]

---

Last modified on October 10, 2021