Analyse – Vectoranalyse – Lijnintegralen

De lijnintegraal van een scalaire functie

Definitie: Als \(f\) een (scalaire) functie is gedefinieerd op een gladde kromme \(\mathcal{C}\) in \(\mathbb{R}^2\) of \(\mathbb{R}^3\) gedefinieerd door de parametrisering \(\mathbf{r}(t)\) met \(a\leq t\leq b\), dan is

\[\int\limits_{\mathcal{C}}f(x,y)\,ds=\int_a^bf(\mathbf{r}(t))|\mathbf{r}'(t)|\,dt\quad\textrm{of}\quad \int\limits_{\mathcal{C}}f(x,y,z)\,ds=\int_a^bf(\mathbf{r}(t))|\mathbf{r}'(t)|\,dt\]

de lijnintegraal van \(f\) langs de kromme \(\mathcal{C}\).

Opmerking: Als \(f\) de constante \(1\) is, dan krijgen we de booglengte: \(L=\displaystyle\int\limits_{\mathcal{C}}ds=\int_a^b|\mathbf{r}'(t)|\,dt\).

Stewart §16.2, Voorbeeld 1
Bereken \(\displaystyle\int\limits_{\mathcal{C}}(2+x^2y)\,ds\), waarbij \(\mathcal{C}\) de bovenste helft is van de eenheidscirkel \(x^2+y^2=1\).

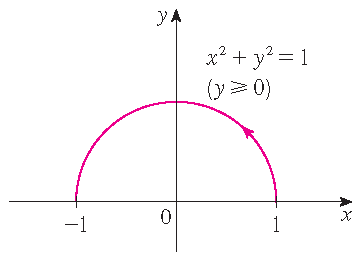
Oplossing: Merk op dat \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) met \(0\leq t\leq \pi\) een (mogelijke) parametrisering is van de kromme \(\mathcal{C}\). Dan geldt \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) en dus \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2}=1\). Dus:

\[\int\limits_{\mathcal{C}}(2+x^2y)\,ds=\int_0^{\pi}(2+\cos^2(t)\sin(t))\cdot1\,dt=\bigg[2t-\frac{1}{3}\cos^3(t)\bigg]_{t=0}^{\pi} =2\pi+\frac{2}{3}.\]

Stewart §16.2, Voorbeeld 5
Bereken \(\displaystyle\int\limits_{\mathcal{C}}y\,\sin(z)\,ds\), waarbij \(\mathcal{C}\) de cirkelvormige helix is gegeven door \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+t\,\mathbf{k}\) met \(0\leq t\leq 2\pi\).

Oplossing: Merk op dat \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}+1\,\mathbf{k}\) en dus \(|\mathbf{r}'(t)|=\sqrt{(-\sin(t))^2+(\cos(t))^2+1^2}=\sqrt{2}\). Dus:

\[\int\limits_{\mathcal{C}}y\,\sin(z)\,ds=\int_0^{2\pi}\sin(t)\,\sin(t)\,\sqrt{2}\,dt=\sqrt{2}\int_0^{2\pi}\sin^2(t)\,dt =\frac{1}{2}\sqrt{2}\int_0^{2\pi}(1-\cos(2t))\,dt=\frac{1}{2}\sqrt{2}\bigg[t-\frac{1}{2}\sin(2t)\bigg]_{y=0}^{2\pi}=\pi\sqrt{2}.\]

Toepassing: fysische interpretatie

Stel dat \(\rho(x,y)\geq 0\) een massadichtheidsfunctie is gedefinieerd in de punten \((x,y)\) van een dunne draad gebogen in de vorm van een kromme \(\mathcal{C}\). Dan is

\[m=\int\limits_{\mathcal{C}}\rho(x,y)\,ds\]

de (totale) massa van de draad. Verder geldt: het massamiddelpunt \((\overline{x},\overline{y})\) wordt gegeven door

\[\overline{x}=\frac{1}{m}\int\limits_{\mathcal{C}}x\,\rho(x,y)\,ds\quad\textrm{en}\quad\overline{y}=\frac{1}{m}\int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds.\]

Stewart §16.2, Voorbeeld 3
Een draad heeft de vorm van de halve cirkel \(x^2+y^2=1\) met \(y\geq 0\). Bepaal het massamiddelpunt van de draad als de massadichtheid gelijk is aan \(\rho(x,y)=k(1-y)\) met \(k\) een constante.

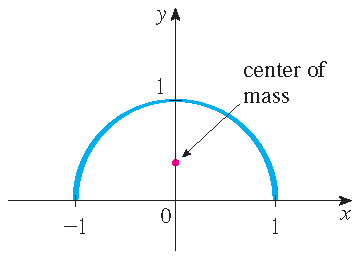
Oplossing: Merk op dat \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) met \(0\leq t\leq \pi\) een (mogelijke) parametrisering is van de kromme \(\mathcal{C}\). Dan geldt

\[m=\int\limits_{\mathcal{C}}\rho(x,y)\,ds=\int\limits_{\mathcal{C}}k(1-y)\,ds=k\int_0^{\pi}(1-\sin(t))\cdot1\,dt =k\bigg[t+\cos(t)\bigg]_{y=0}^{\pi}=k(\pi-2).\]

Uit de symmetrie van zowel de draad als de massadichtheidsfunctie volgt dat \(\overline{x}=0\). Verder geldt dat

\begin{align*} \int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds&=\int\limits_{\mathcal{C}}k\,y(1-y)\,ds=k\int_0^{\pi}\sin(t)(1-\sin(t))\cdot1\,dt =k\int_0^{\pi}\left(\sin(t)-\frac{1}{2}+\frac{1}{2}\cos(2t)\right)\,dt\\[2.5mm] &=k\bigg[-\cos(t)-\frac{1}{2}t+\frac{1}{4}\sin(2t)\bigg]_{y=0}^{\pi}=k\left(2-\tfrac{1}{2}\pi\right). \end{align*}

Hieruit volgt dat \(\overline{y}=\displaystyle\frac{1}{m}\int\limits_{\mathcal{C}}y\,\rho(x,y)\,ds=\frac{4-\pi}{2(\pi-2)}\approx0.376\).

Opmerking: Evenzo (uiteraard) voor (ruimte)krommen in \(\mathbb{R}^3\).

De lijnintegraal van een vectorveld

Definitie: Laat \(\mathbf{F}\) een continu vectorveld zijn gedefinieerd op een gladde kromme gegeven door een vectorfunctie \(\mathbf{r}(t)\) met \(a\leq t\leq b\). Dan is

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int_a^b\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt\]

de lijnintegraal van \(\mathbf{F}\) langs de kromme \(\mathcal{C}\).

Deze lijnintegraal definieert de arbeid verricht door het krachtveld \(\mathbf{F}\) bij de verplaasting van een deeltje langs de kromme \(\mathcal{C}\) van \(\mathbf{r}(a)\) tot \(\mathbf{r}(b)\).

Stewart §16.2, Voorbeeld 7
Bepaal de arbeid verricht door het krachtveld \(\mathbf{F}(x,y)=x^2\,\mathbf{i}-xy\,\mathbf{j}\) bij de verplaasting van een deeltje langs de kwart cirkel \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j},\; 0\leq t\leq\frac{1}{2}\pi\).

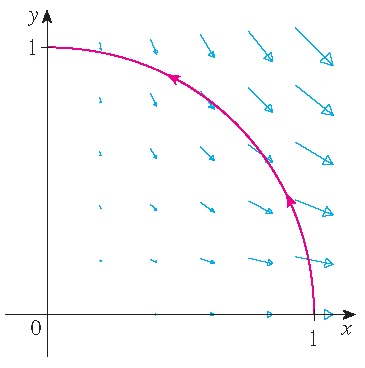
Oplossing: Merk op dat \(\mathbf{r}'(t)=-\sin(t)\,\mathbf{i}+\cos(t)\,\mathbf{j}\) en dus

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^{\frac{1}{2}\pi}\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^{\frac{1}{2}\pi}\langle \cos^2(t),-\cos(t)\sin(t) \rangle\cdot\langle -\sin(t),\cos(t) \rangle\,dt\\[2.5mm] &=\int_0^{\frac{1}{2}\pi}\left(-2\cos^2(t)\sin(t)\right)\,dt=\frac{2}{3}\cos^3(t)\bigg|_0^{\frac{1}{2}\pi}=-\frac{2}{3}. \end{align*}

Opmerking: Het teken van een lijnintegraal van een vectorveld hangt af van de oriëntatie van de kromme: \(\displaystyle\int\limits_{\mathcal{-C}}\mathbf{F}\cdot d\mathbf{r}=-\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\).

Stewart §16.2, Voorbeeld 8
Bereken \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), waarbij \(\mathbf{F}(x,y,z)=xy\,\mathbf{i}+yz\,\mathbf{j}+xz\,\mathbf{k}\) en \(\mathcal{C}\) is de kromme gegeven door \(\mathbf{r}(t)=t\,\mathbf{i}+t^2\,\mathbf{j}+t^3\,\mathbf{k}\) met \(0\leq t\leq 1\).

Oplossing: Merk op dat \(\mathbf{r}'(t)=1\,\mathbf{i}+2t\,\mathbf{j}+3t^2\,\mathbf{k}\) en dus

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^1\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^1\langle t^3,t^5,t^4 \rangle\cdot\langle 1,2t,3t^2 \rangle\,dt=\int_0^1\left(t^3+2t^6+3t^6\right)\,dt\\[2.5mm] &=\bigg[\frac{1}{4}t^4+\frac{5}{7}t^7\bigg]_{t=0}^1=\frac{1}{4}+\frac{5}{7}=\frac{7+20}{28}=\frac{27}{28}. \end{align*}

Notatie: Als \(\mathbf{F}=\langle P,Q \rangle\) in \(\mathbb{R}^2\), dan: \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}P\,dx+Q\,dy\). Als \(\mathbf{F}=\langle P,Q,R \rangle\) in \(\mathbb{R}^3\), dan: \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}P\,dx+Q\,dy+R\,dz\).

---

Laatst gewijzigd op 9 oktober 2021