Analyse – Vectoranalyse – De stelling van Stokes

De stelling van Stokes kan worden gezien als een hogerdimensionale versie van de stelling van Green. Waar de stelling van Green een tweevoudige integraal over een gebied \(D\) in het platte vlak relateert aan een lijnintegraal over de vlakke randkromme van \(D\), daar relateert de stelling van Stokes een oppervlakintegraal over een oppervlak \(S\) aan een lijnintegraal over de rand(ruimte)kromme van \(S\).

Oriëntatie

Beschouw een georiënteerd oppervlak \(S\) met eenheidsnormaalvector \(\mathbf{n}\).

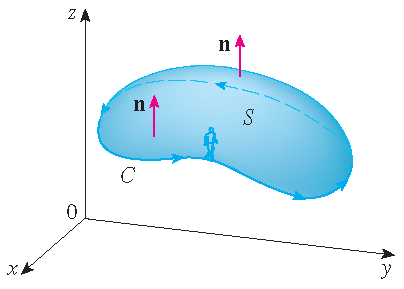
De oriëntatie van \(S\) induceert de positieve oriëntatie van de randkromme \(\mathcal{C}\).

Stelling: Laat \(S\) een georiënteerd stuksgewijs glas oppervlak zijn dat begrensd wordy door een enkelvoudig gesloten stuksgewijs gladde randkromme \(\mathcal{C}\) met positieve oriëntatie. Laat \(\mathbf{F}\) een vecterveld zijn waarvan de componenten continue partiële afgeleiden hebben op een open gebied in \(\mathbb{R}^3\) dat \(S\) bevat. Dan geldt

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\iint\limits_S\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}.\]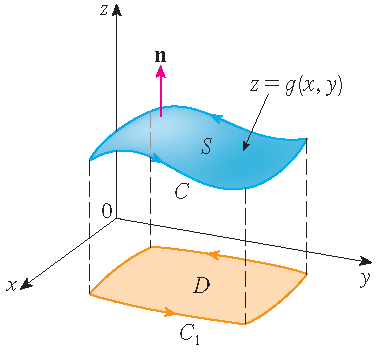

Bewijs (alleen voor de grafiek van een functie): We nemen aan dat \(S\) de grafiek is van een functie \(g(x,y)\) met domein \(D\), waarbij \(g\) continue tweede-orde partiële afgeleiden heeft en \(D\) een regulier vlak gebied is waarvan de randkromme \(\mathcal{C}_1\) correspondeert met \(\mathcal{C}\). Als de oriëntatie van \(S\) naar boven gericht is, dan correspondeert de positieve oriëntatie van \(\mathcal{C}\) met de positieve oriëntatie van \(\mathcal{C}_1\). We gaan er tevens uit dat \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\), waarbij de partiële afgeleiden van \(P\), \(Q\) en \(R\) continu zijn. Omdat

\[\textrm{rot}\,\mathbf{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\,\mathbf{i} +\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\,\mathbf{j} +\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,\mathbf{k}\]

en

\[S:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+g(x,y)\,\mathbf{k}\quad\Longrightarrow\quad \mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,\frac{\partial g}{\partial x}\rangle\times\langle 0,1,\frac{\partial g}{\partial y}\rangle =\langle-\frac{\partial g}{\partial x},-\frac{\partial g}{\partial y},1\rangle,\]

geldt dat (merk op dat deze normaalvector naar boven gericht is)

\[\iint\limits_S\textrm{rotl}\,\mathbf{F}\cdot d\mathbf{S} =\iint\limits_D\left(-\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\frac{\partial z}{\partial x} -\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\frac{\partial z}{\partial y} +\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA,\]

waarbij de partiële afgeleiden van \(P\), \(Q\) en \(R\) genomen worden in \((x,y,g(x,y))\).

Als \(\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}\) met \(a\leq t\leq b\) een parametrisering van \(\mathcal{C}_1\) is, dan is een parametervoorstelling van \(\mathcal{C}\) gelijk aan

\[\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}+g(x(t),y(t))\,\mathbf{k},\quad a\leq t\leq b.\]

Dus volgt met behulp van de kettingregel en de stelling van Green

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_a^b\left(P\frac{dx}{dt}+Q\frac{dy}{dt}+R\frac{dz}{dt}\right)\,dt =\int_a^b\left(P\,\frac{dx}{dt}+Q\,\frac{dy}{dt}+R\,\left(\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}\right)\right)\,dt\\[2.5mm] &=\int_a^b\left(\left(P+R\frac{\partial z}{\partial x}\right)\frac{dx}{dt}+\left(Q+R\frac{\partial z}{\partial y}\right)\frac{dy}{dt}\right)\,dt =\int\limits_{\mathcal{C}_1}\left(P+R\,\frac{\partial z}{\partial x}\right)\,dx+\left(Q+R\,\frac{\partial z}{\partial y}\right)\,dy\\[2.5mm] &=\iint\limits_D\left(\frac{\partial}{\partial x}\left(Q+R\frac{\partial z}{\partial y}\right) -\frac{\partial}{\partial y}\left(P+R\frac{\partial z}{\partial x}\right)\right)\,dA. \end{align*}

Merk op dat \(P\), \(Q\) en \(R\) functies zijn van \(x\), \(y\) en \(z\) en dat \(z=g(x,y)\) zelf een functie van \(x\) en \(y\) is. Dus volgt, met behulp van de kettingregel, dat

\[\frac{\partial}{\partial x}\left(Q+R\,\frac{\partial z}{\partial y}\right) =\frac{\partial Q}{\partial x}+\frac{\partial Q}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial R}{\partial x}\frac{\partial z}{\partial y} +\frac{\partial R}{\partial z}\frac{\partial z}{\partial x}\frac{\partial z}{\partial y}+R\frac{\partial^2z}{\partial x\,\partial y}\]

en

\[\frac{\partial}{\partial y}\left(P+R\,\frac{\partial z}{\partial x}\right) =\frac{\partial P}{\partial y}+\frac{\partial P}{\partial z}\frac{\partial z}{\partial y}+\frac{\partial R}{\partial y}\frac{\partial z}{\partial x} +\frac{\partial R}{\partial z}\frac{\partial z}{\partial y}\frac{\partial z}{\partial x}+R\frac{\partial^2z}{\partial y\,\partial x}.\]

Dus volgt, met behulp van de stelling van Clairaut, dat

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\iint\limits_D\left(-\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\frac{\partial z}{\partial x} -\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\frac{\partial z}{\partial y} +\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA.\]

Dit bewijst de stelling.

Stewart §16.8, Voorbeeld 1
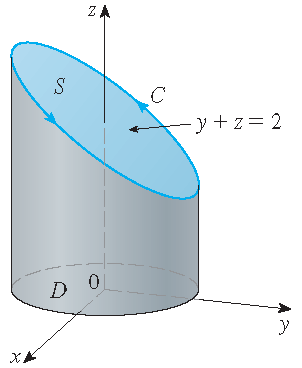
Bereken \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), waarbij \(\mathbf{F}(x,y,z)=-y^2\,\mathbf{i}+x\,\mathbf{j}+z^2\,\mathbf{k}\) en \(\mathcal{C}\) de snijkromme is van het vlak \(y+z=2\) en de cilinder \(x^2+y^2=1\) die van boven af gezien tegen de wijzers van de klok in wordt doorlopen.

Oplossing: De kromme \(\mathcal{C}\) is de ellips die getoond wordt in het plaatje. Een parametrisering is

\[\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+\left(2-\sin(t)\right)\,\mathbf{k},\quad 0\leq t\leq 2\pi.\]

Een directe berekening zou dus zijn

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^{2\pi}\langle -\sin^2(t),\cos(t),\left(2-\sin(t)\right)^2\rangle\cdot \langle -\sin(t),\cos(t),-\cos(t)\rangle\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\sin^3(t)+\cos^2(t)-\cos(t)\left(2-\sin(t)\right)^2\right)\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\sin(t)\left(1-\cos^2(t)\right)+\frac{1}{2}+\frac{1}{2}\cos(2t)-\cos(t)\left(2-\sin(t)\right)^2\right)\,dt\\[2.5mm] &=\bigg[-\cos(t)+\frac{1}{3}\cos^3(t)+\frac{1}{2}t+\frac{1}{4}\sin(2t)+\frac{1}{3}\left(2-\sin(t)\right)^3\bigg]_{t=0}^{2\pi}=\pi. \end{align*}

Met behulp van

\[\textrm{rot}\,\mathbf{F}=(0-0)\,\mathbf{i}+(0-0)\,\mathbf{j}+(1+2y)\,\mathbf{k}=(1+2y)\,\mathbf{k}\]

volgt uit de stelling van Stokes, met behulp van poolcoördinaten, dat

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\iint\limits_S\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S} =\iint\limits_D(1+2y)\,dA=\int_0^{2\pi}\int_0^1\left(1+2r\sin(\theta)\right)\,r\,dr\,d\theta =\int_0^{2\pi}\bigg[\frac{1}{2}r^2+\frac{2}{3}r^3\sin(\theta)\bigg]_{r=0}^1\,d\theta\\[2.5mm] &=\int_0^{2\pi}\left(\frac{1}{2}+\frac{2}{3}\sin(\theta)\right)\,d\theta =\bigg[\frac{1}{2}\theta-\frac{2}{3}\cos(\theta)\bigg]_{\theta=0}^{2\pi}=\pi. \end{align*}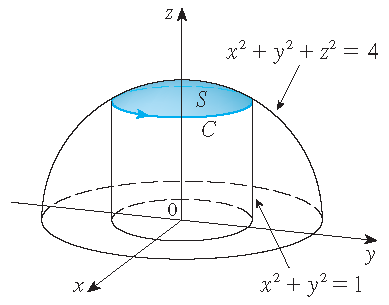

Stewart §16.8, Voorbeeld 2
Gebruik de stelling van Stokes om de integraal \(\displaystyle\iint\limits_S\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}\) te berekenen, waarbij \(\mathbf{F}(x,y,z)=xz\,\mathbf{i}+yz\,\mathbf{j}+xy\,\mathbf{k}\) en \(S\) het deel is van de bol \(x^2+y^2+z^2=4\) dat binnen de cilinder \(x^2+y^2=1\) ligt en boven het \(xy\)-vlak.

Oplossing: Om de randkromme \(\mathcal{C}\) te vinden lossen we de vergelijkingen \(x^2+y^2+z^2=4\) en \(x^2+y^2=1\). Aftrekken geeft \(z^2=3\) en dus \(z=\sqrt{3}\) (want \(z>0\)). Dus: \(\mathcal{C}\) is de cirkel gegeven door \(x^2+y^2=1\) en \(z=\sqrt{3}\). Een parametrisering van \(\mathcal{C}\) is dus

\[\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+\sqrt{3}\,\mathbf{k},\quad 0\leq t\leq 2\pi.\]

Dus volgt uit de stelling van Stokes dat

\begin{align*} \iint\limits_S\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}&=\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\int_0^{2\pi}\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^{2\pi}\langle \sqrt{3}\cos(t),\sqrt{3}\sin(t),\cos(t)\sin(t)\rangle\cdot\langle -\sin(t),\cos(t),0\rangle\,dt\\[2.5mm] &=\int_0^{2\pi}\left(-\sqrt{3}\sin(t)\cos(t)+\sqrt{3}\sin(t)\cos(t)+0\right)\,dt=0. \end{align*}

Voorbeeld: vergelijk met Stewart §16.8, Opgave 1
Laat \(H\) de halve bol \(x^2+y^2+z^2=4\) met \(z\geq 0\) zijn en \(P\) het deel van de paraboloïde \(z=4-x^2-y^2\) met \(z\geq 0\). Als \(\mathbf{F}\) een vectorveld is op \(\mathbb{R}^3\) waarvan de componenten continue partiële afgeleiden hebben, toon dan aan dat

\[\iint\limits_H\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}=\iint\limits_P\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}.\]

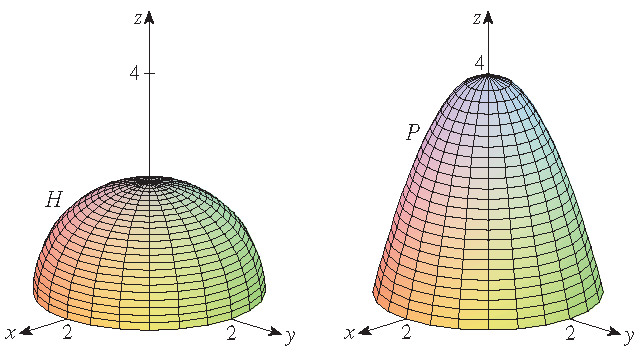
Oplossing: Merk op dat de cirkel \(\mathcal{C}\) gegeven door \(x^2+y^2=4\) en \(z=0\) de randkromme is van beide oppervlakken \(H\) en \(P\). Nemen we de oriëntatie geïnduceerd door die van beide oppervlakken, dan volgt uit de stelling van Stokes dat

\[\iint\limits_H\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}=\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\iint\limits_P\textrm{rot}\,\mathbf{F}\cdot d\mathbf{S}.\]

---

Laatst gewijzigd op 19 oktober 2021