Analyse – Vectoranalyse – Toepassingen

Als een gevolg van de stelling van Green kunnen we nu bewijzen:

Stelling: Laat \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) een vectorveld zijn op een open enkelvoudig samenhangend gebied \(D\). Neem aan dat \(P\) en \(Q\) continue eerste-orde partiële afgeleiden hebben en dat

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{overal op}\quad D.\]

Dan is \(\mathbf{F}\) conservatief.

Bewijs: Als \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) een vectorveld is op een open enkelvoudig samenhangend gebied \(D\), \(P\) en \(Q\) hebben continue eerste-orde partiële afgeleiden en

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{overal op}\quad D,\]

dan geldt dat

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\oint\limits_{\mathcal{C}}P\,dx+Q\,dy =\iint\limits_R\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA=\iint\limits_R0\,dA=0\]

voor elke enkelvoudig gesloten kromme \(\mathcal{C}\) in \(D\) dat het gebied \(R\) omsluit. Een kromme die niet enkelvoudig is, snijdt zichzelf in één of meer punten en kan worden opgedeeld in meerdere enkelvoudig gesloten krommen. De lijnintegralen van \(\mathbf{F}\) over al deze enkelvoudig gesloten krommen zijn gelijk aan nul, waaruit volgt dat \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) voor elke gesloten kromme \(\mathcal{C}\) in \(D\). Dit bewijst dat \(\mathbf{F}\) conservatief is.

Als een toepassing hebben we al gezien hoe we de oppervlakte kunnen berekenen van het gebied ingesloten door een ellips. Nu kunnen we ook de oppervlakte onder een boog van een cycloïde bepalen en de oppervlakte van een gebied ingesloten door een cardioïde.

1) Beschouw de cycloïde gegeven door de parametrisering \(\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j}\) met \(0\leq t\leq 2\pi\).

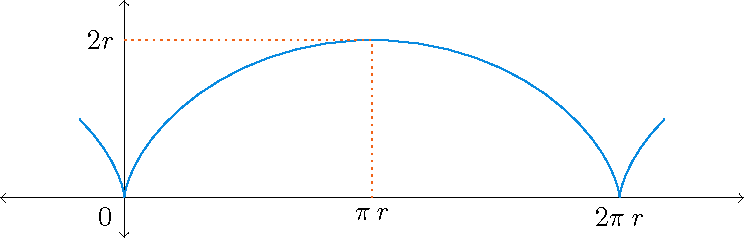
We hebben gezien dat de booglengte van deze enkele boog van de cycloïde gelijk is aan \(8r\).

Nu kan de stelling van Green worden gebruikt om de oppervlakte onder deze enkele boog van de cycloïde (boven de \(x\)-as) te bepalen. Deze oppervlakte is gelijk aan \(\displaystyle\int\limits_{\mathcal{C}}x\,dy\), waarbij \(\mathcal{C}\) de randkromme \(\mathcal{C}=\mathcal{C}_1\cup\mathcal{C}_2\) is met

\[\mathcal{C}_1:\quad\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j},\quad 0\leq t\leq 2\pi\]

en

\[\mathcal{C}_2:\quad\mathbf{r}(t)=2\pi r(1-t)\,\mathbf{i},\quad 0\leq t\leq 1.\]

Merk op dat de oriëntatie van deze randkromme negatief is. Hieruit volgt dat de oppervlakte onder een boog van de cycloïde gelijk is aan

\[-\int\limits_{\mathcal{C}}x\,dy=-\int\limits_{\mathcal{C}_1}x\,dy-\int\limits_{\mathcal{C}_2}x\,dy =-\int\limits_{\mathcal{C}_1}x\,dy-0=-\int\limits_{\mathcal{C}_1}x\,dy\]

en dus

\[\int\limits_{\mathcal{C}}x\,dy=\int\limits_{\mathcal{C}_1}x\,dy=\int_0^{2\pi}r(t-\sin(t))\,d\,r(1-\cos(t)) =r^2\int_0^{2\pi}(t-\sin(t))\cdot\sin(t)\,dt=r^2\int_0^{2\pi}t\sin(t)\,dt-r^2\int_0^{2\pi}\sin^2(t)\,dt.\]

Nu geldt

\[\int_0^{2\pi}t\sin(t)\,dt=-\int_0^{2\pi}t\,d\cos(t)=-t\cos(t)\bigg|_{t=0}^{2\pi}+\int_0^{2\pi}\cos(t)\,dt =-2\pi+\sin(t)\bigg|_{t=0}^{2\pi}=-2\pi+0=-2\pi\]

en

\[\int_0^{2\pi}\sin^2(t)\,dt=\frac{1}{2}\int_0^{2\pi}\left(1-\cos(2t)\right)\,dt =\frac{1}{2}\bigg[t-\frac{1}{2}\sin(2t)\bigg]_{t=0}^{2\pi}=\pi.\]

Hieruit volgt dat de oppervlakte gelijk is aan

\[-\int\limits_{\mathcal{C}}x\,dy=-r^2\int_0^{2\pi}t\sin(t)\,dt+r^2\int_0^{2\pi}\sin^2(t)\,dt=2\pi\,r^2+\pi\,r^2=3\pi\,r^2.\]

2) Beschouw de cardioïde die in poolcoördinaten wordt gegeven door \(r=2+2\cos(\theta)\):

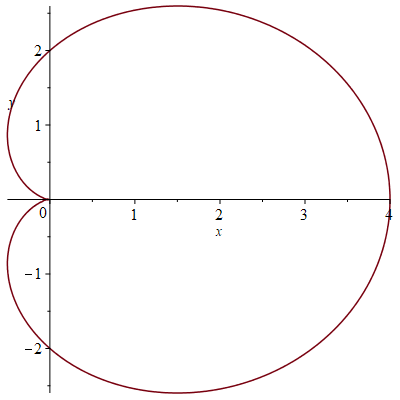
Een parametrisering is: \(\mathbf{r}(t)=(2+2\cos(t))\cos(t)\,\mathbf{i}+(2+2\cos(t))\sin(t)\,\mathbf{j}\) met \(0\leq t\leq 2\pi\).

We hebben gezien dat de booglengte van deze kromme \(16\) is. Nu kan de stelling van Green worden gebruikt om de oppervlakte te vinden van het gebied ingesloten door deze cardioïde. Omdat de oriëntatie positief is, is deze oppervlakte gelijk aan

\begin{align*} \oint\limits_{\mathcal{C}}x\,dy&=\int_0^{2\pi}(2+2\cos(t))\cos(t)\,d(2+2\cos(t))\sin(t) =\int_0^{2\pi}(2+2\cos(t))\cos(t)\cdot\left((2+2\cos(t))\cos(t)-2\sin^2(t)\right)\,dt\\[2,5mm] &=\ldots=\int_0^{2\pi}\left(8\cos^4(t)+12\cos^3(t)-\cos(t)\right)\,dt. \end{align*}

Nu geldt

\[\int_0^{2\pi}\cos(t)\,dt=\bigg[\sin(t)\bigg]_{t=0}^{\pi}=0,\quad\int_0^{2\pi}\cos^3(t)\,dt=\int_0^{2\pi}\cos(t)\left(1-\sin^2(t)\right)\,dt =\bigg[\sin(t)-\frac{1}{3}\sin^3(t)\bigg]_{t=0}^{\pi}=0\]

en

\begin{align*} \int_0^{2\pi}\cos^4(t)\,dt&=\int_0^{2\pi}\left(\frac{1}{2}+\frac{1}{2}\cos(2t)\right)^2\,dt =\int_0^{2\pi}\left(\frac{1}{4}+\frac{1}{2}\cos(2t)+\frac{1}{4}\cos^2(2t)\right)\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\frac{1}{4}+\frac{1}{2}\cos(2t)+\frac{1}{4}\left(\frac{1}{2}+\frac{1}{2}\cos(4t)\right)\right)\,dt =\int_0^{2\pi}\left(\frac{3}{8}+\frac{1}{2}\cos(2t)+\frac{1}{8}\cos(4t)\right)\,dt\\[2.5mm] &=\bigg[\frac{3}{8}t+\frac{1}{4}\sin(2t)+\frac{1}{32}\sin(4t)\bigg]_{t=0}^{\pi}=\frac{3}{4}\pi, \end{align*}

waaruit volgt dat de oppervlakte gelijk is aan

\[\oint\limits_{\mathcal{C}}x\,dy=8\cdot\frac{3}{4}\pi=6\pi.\]

---

Laatst gewijzigd op 13 oktober 2021