Calculus – Vector calculus – Applications

As a consequence of Green's theorem we can now prove:

Theorem: Let \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) be a vector field on an open simply-connected region \(D\). Suppose that \(P\) and \(Q\) have continuous first-order partial derivatives and

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{throughout}\quad D.\]

Then \(\mathbf{F}\) is conservative.

Proof: If \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) is a vector field on an open simply-connected region \(D\), \(P\) and \(Q\) have continuous first-order partial derivatives and

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{throughout}\quad D,\]

then

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\oint\limits_{\mathcal{C}}P\,dx+Q\,dy =\iint\limits_R\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA=\iint\limits_R0\,dA=0\]

for every simple closed curve \(\mathcal{C}\) in \(D\) that encloses the region \(R\). A curve that is not simple crosses itself at one or more points and can be broken up into a number of simple closed curves. The line integrals of \(\mathbf{F}\) over all these simple closed curves equal zero, which shows that \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) for every closed curve \(\mathcal{C}\) in \(D\). This proves that \(\mathbf{F}\) is conservative.

As an application we have already seen that we can find the area of the region enclosed by an ellipse. Now we can also find the area under one arch of a cycloid and the area of a region enclosed by a cardioid.

1) Recall the cycloid given by the parametrization \(\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j}\) with \(0\leq t\leq 2\pi\).

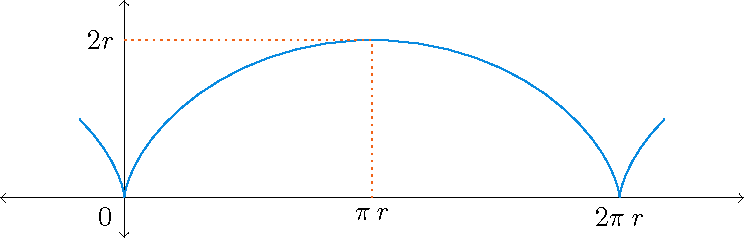
We have seen that the arc length of this single arch of the cycloid is \(8r\).

Now Green's theorem can be used to find the area under this single arch of the cycloid (above the \(x\)-axis). This area equals \(\displaystyle\int\limits_{\mathcal{C}}x\,dy\), where \(\mathcal{C}\) denotes the boundary curve \(\mathcal{C}=\mathcal{C}_1\cup\mathcal{C}_2\) with

\[\mathcal{C}_1:\quad\mathbf{r}(t)=r(t-\sin(t))\,\mathbf{i}+r(1-\cos(t))\,\mathbf{j},\quad 0\leq t\leq 2\pi\]

and

\[\mathcal{C}_2:\quad\mathbf{r}(t)=2\pi r(1-t)\,\mathbf{i},\quad 0\leq t\leq 1.\]

Note that the orientation of this boundary curve is negative. This implies that the area under the arch of the cycloid is

\[-\int\limits_{\mathcal{C}}x\,dy=-\int\limits_{\mathcal{C}_1}x\,dy-\int\limits_{\mathcal{C}_2}x\,dy =-\int\limits_{\mathcal{C}_1}x\,dy-0=-\int\limits_{\mathcal{C}_1}x\,dy\]

and therefore

\[\int\limits_{\mathcal{C}}x\,dy=\int\limits_{\mathcal{C}_1}x\,dy=\int_0^{2\pi}r(t-\sin(t))\,d\,r(1-\cos(t)) =r^2\int_0^{2\pi}(t-\sin(t))\cdot\sin(t)\,dt=r^2\int_0^{2\pi}t\sin(t)\,dt-r^2\int_0^{2\pi}\sin^2(t)\,dt.\]

Now we have

\[\int_0^{2\pi}t\sin(t)\,dt=-\int_0^{2\pi}t\,d\cos(t)=-t\cos(t)\bigg|_{t=0}^{2\pi}+\int_0^{2\pi}\cos(t)\,dt =-2\pi+\sin(t)\bigg|_{t=0}^{2\pi}=-2\pi+0=-2\pi\]

and

\[\int_0^{2\pi}\sin^2(t)\,dt=\frac{1}{2}\int_0^{2\pi}\left(1-\cos(2t)\right)\,dt =\frac{1}{2}\bigg[t-\frac{1}{2}\sin(2t)\bigg]_{t=0}^{2\pi}=\pi.\]

This implies that the area equals

\[-\int\limits_{\mathcal{C}}x\,dy=-r^2\int_0^{2\pi}t\sin(t)\,dt+r^2\int_0^{2\pi}\sin^2(t)\,dt=2\pi\,r^2+\pi\,r^2=3\pi\,r^2.\]

2) Recall the cardioid in polar coordinates given by \(r=2+2\cos(\theta)\):

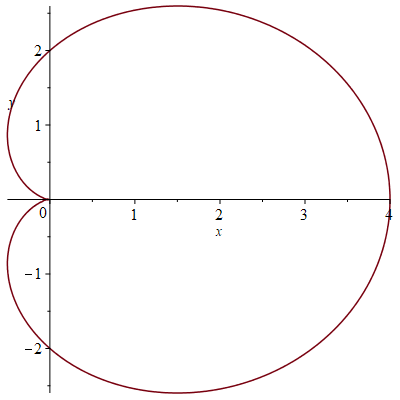
A parametrization is: \(\mathbf{r}(t)=(2+2\cos(t))\cos(t)\,\mathbf{i}+(2+2\cos(t))\sin(t)\,\mathbf{j}\) with \(0\leq t\leq 2\pi\).

We have seen that the arc length of this curve is \(16\). Now Green's theorem can be used to find the area of the region enclosed by this cardioid. Because of the positive orientation, this area equals

\begin{align*} \oint\limits_{\mathcal{C}}x\,dy&=\int_0^{2\pi}(2+2\cos(t))\cos(t)\,d(2+2\cos(t))\sin(t) =\int_0^{2\pi}(2+2\cos(t))\cos(t)\cdot\left((2+2\cos(t))\cos(t)-2\sin^2(t)\right)\,dt\\[2,5mm] &=\ldots=\int_0^{2\pi}\left(8\cos^4(t)+12\cos^3(t)-\cos(t)\right)\,dt. \end{align*}

Now we have

\[\int_0^{2\pi}\cos(t)\,dt=\bigg[\sin(t)\bigg]_{t=0}^{\pi}=0,\quad\int_0^{2\pi}\cos^3(t)\,dt=\int_0^{2\pi}\cos(t)\left(1-\sin^2(t)\right)\,dt =\bigg[\sin(t)-\frac{1}{3}\sin^3(t)\bigg]_{t=0}^{\pi}=0\]

and

\begin{align*} \int_0^{2\pi}\cos^4(t)\,dt&=\int_0^{2\pi}\left(\frac{1}{2}+\frac{1}{2}\cos(2t)\right)^2\,dt =\int_0^{2\pi}\left(\frac{1}{4}+\frac{1}{2}\cos(2t)+\frac{1}{4}\cos^2(2t)\right)\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\frac{1}{4}+\frac{1}{2}\cos(2t)+\frac{1}{4}\left(\frac{1}{2}+\frac{1}{2}\cos(4t)\right)\right)\,dt =\int_0^{2\pi}\left(\frac{3}{8}+\frac{1}{2}\cos(2t)+\frac{1}{8}\cos(4t)\right)\,dt\\[2.5mm] &=\bigg[\frac{3}{8}t+\frac{1}{4}\sin(2t)+\frac{1}{32}\sin(4t)\bigg]_{t=0}^{\pi}=\frac{3}{4}\pi, \end{align*}

which implies that the area equals

\[\oint\limits_{\mathcal{C}}x\,dy=8\cdot\frac{3}{4}\pi=6\pi.\]

---

Last modified on October 13, 2021