Calculus – Vector calculus – Vector fields

Definition: Let \(D\) be a set in \(\mathbb{R}^2\). A vector field on \(\mathbb{R}^2\) is a function \(\mathbf{F}\) that assigns to each point \((x,y)\) in \(D\) a two-dimensional vector \(\mathbf{F}(x,y)\).

Notation: \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}=\langle P,Q \rangle\).

The functions \(P(x,y)\) and \(Q(x,y)\) are called the component functions of the vector field \(\mathbf{F}(x,y)\).

Stewart §16.1, Example 1
A vector field on \(\mathbb{R}^2\) is defined by \(\mathbf{F}(x,y)=-y\,\mathbf{i}+x\,\mathbf{j}\). Describe \(\mathbf{F}\) by sketching some of the vectors \(\mathbf{F}(x,y)\).

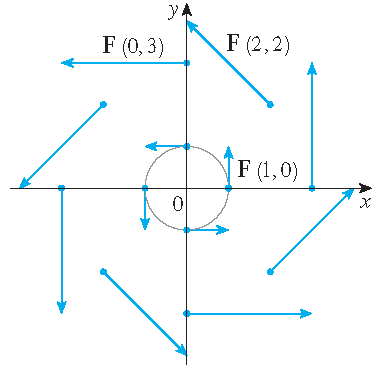
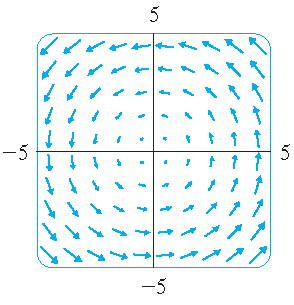
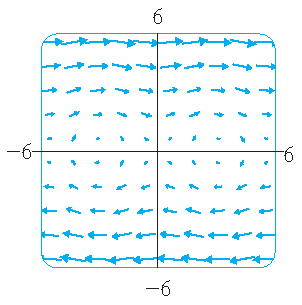
More examples:

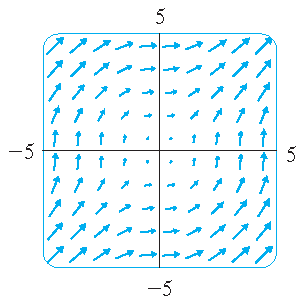\(\mathbf{F}(x,y)=\langle -y,x \rangle\)	\(\mathbf{F}(x,y)=\langle y,\sin(x) \rangle\)	\(\mathbf{F}(x,y)=\langle \ln(1+y^2),\ln(1+x^2) \rangle\)

Definition: Let \(E\) be a subset of \(\mathbb{R}^3\). A vector field on \(\mathbb{R}^3\) is a function \(\mathbf{F}\) that assigns to each point \((x,y,z)\) in \(E\) a three-dimensional vector \(\mathbf{F}(x,y,z)\).

Notation: \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}=\langle P,Q,R \rangle\).

The functions \(P(x,y,z)\), \(Q(x,y,z)\) and \(R(x,y,z)\) are called the component functions of the vector field \(\mathbf{F}(x,y,z)\).

Examples:

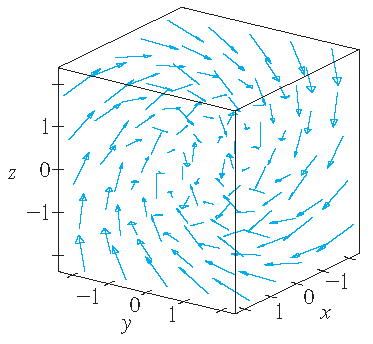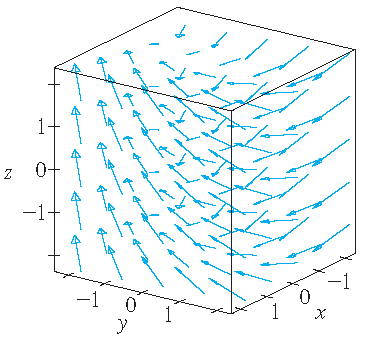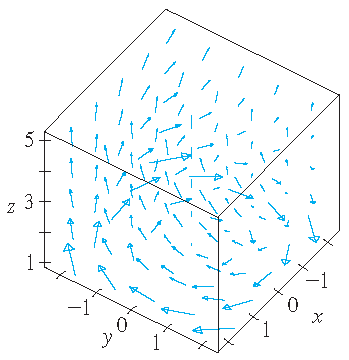\(\mathbf{F}(x,y,z)=\langle y,z,x \rangle\)	\(\mathbf{F}(x,y,z)=\langle y,-2,x \rangle\)	\(\mathbf{F}(x,y,z)=\langle \frac{y}{z},-\frac{x}{z},\frac{z}{4} \rangle\)

Examples of a vector field:

• velocity field (of a fluid or a gas);


• gravitational field;


• force field;


• electric field;


• gradient vector field.

See also these examples of vector fields from daily life.

Gradient (vector) field

Definition: If \(f\) is a scalar function of two variables, then

\[\nabla f(x,y)=f_x(x,y)\,\mathbf{i}+f_y(x,y)\,\mathbf{j}\]

is a gradient (vector) field on \(\mathbb{R}^2\).

Likewise, if \(f\) is a scalar function of three variables, then

\[\nabla f(x,y,z)=f_x(x,y,z)\,\mathbf{i}+f_y(x,y,z)\,\mathbf{j}+f_z(x,y,z)\,\mathbf{k}\]

is a gradient (vector) field on \(\mathbb{R}^3\).

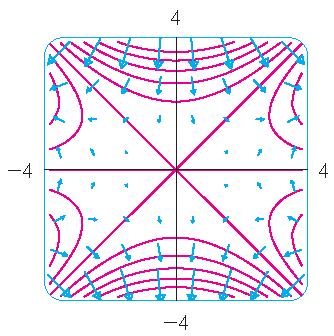Stewart §16.1, Example 6
Find the gradient vector field of \(f(x,y)=x^2y-y^3\). Plot the gradient vector field together with a contour map of \(f\). How are they related?

Solution: The gradient vector field is given by

\[\nabla f(x,y)=\langle f_x(x,y),f_y(x,y) \rangle=\langle 2xy,x^2-3y^2 \rangle.\]

The picture shows a contour map of \(f\) with the gradient vector field. The gradient vectors are perpendicular to the level curves. Moreover, the gradient vectors are long where the level curves are close to each other and short where the curves are farther apart. That's because the length of the gradient vector is the value of the directional derivative of \(f\) and closely spaced level curves indicate a steep graph.

Conservative vector fields

Definition: A vector field \(\mathbf{F}\) is called a conservative vector field if it is the gradient of some scalar function, that is, if there exists a function \(f\) such that \(\mathbf{F}=\nabla f\). Such a function \(f\) is called a potential function for \(\mathbf{F}\).

---

Last modified on October 7, 2021