Calculus – Vector calculus – Surface integrals

The surface integral of a scalar function

Suppose that \(f\) is a function of three variables whose domain includes a surface \(S\) given by the vector function

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D.\]

We first assume that \(D\) is a rectangle and we divide it into subrectangles \(R_{ij}\) with dimensions \(\Delta u\) and \(\Delta v\). Then the surface \(S\) is divided into corresponding patches \(S_{ij}\). We evaluate \(f\) at a point \(P_{ij}^*\) in each patch, multiply by the area \(\Delta S_{ij}\) of the patch and form the Riemann sum

\[\sum_{i=1}^m\sum_{j=1}^nf(P_{ij}^*)\Delta S_{ij}.\]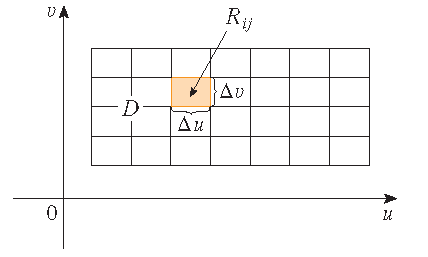

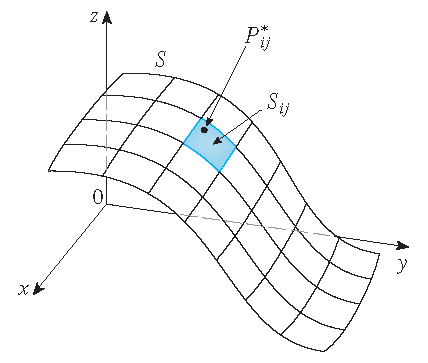Then we take the limit as the number of patches increases and define the surface integral of \(f\) over the suraface \(S\) as

\[\iint\limits_Sf(x,y,z)\,dS=\lim\limits_{m\to\infty}\lim\limits_{n\to\infty}\sum_{i=1}^m\sum_{j=1}^nf(P_{ij}^*)\Delta S_{ij}.\]

Note that the special case \(f(x,y,z)=1\) defines the area of the surface \(S\). So we proceed in the same way by approximating the area of the patch \(S_{ij}\) by the area of an approximating parallelogram in the tangent plane.

Definition: If a smooth parametric surface \(S\) is given by

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad (u,v)\in D\]

and \(S\) is covered just once as \((u,v)\) ranges throughout \(D\), then the surface integral of \(f\) over the surface \(S\) is

\[\iint\limits_Sf(x,y,z)\,dS=\iint\limits_Df(\mathbf{r}(u,v))\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA,\]

where \(\displaystyle\mathbf{r}_u=\frac{\partial x}{\partial u}\,\mathbf{i}+\frac{\partial y}{\partial u}\,\mathbf{j}+\frac{\partial z}{\partial u}\,\mathbf{k}\) and \(\displaystyle\mathbf{r}_v=\frac{\partial x}{\partial v}\,\mathbf{i}+\frac{\partial y}{\partial v}\,\mathbf{j}+\frac{\partial z}{\partial v}\,\mathbf{k}\).

Stewart §16.7, Example 1
Evaluate the surface integral \(\displaystyle\iint\limits_Sx^2\,dS\), where \(S\) is the unit sphere \(x^2+y^2+z^2=1\).

Solution: A parametrization of \(S\) is

\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k},\quad 0\leq\phi\leq\pi,\quad 0\leq\theta\leq 2\pi.\]

Then we have as before

\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\quad\Longrightarrow\quad \left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|=\sin(\phi)\geq 0.\]

Hence we have with \(D=\{(\phi,\theta)\,|\,0\leq\phi\leq\pi,\;0\leq\theta\leq2\pi\}\)

\begin{align*} \iint\limits_Sx^2\,dS&=\iint\limits_D\sin^2(\phi)\cos^2(\theta)\,\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|\,dA =\int_0^{2\pi}\int_0^{\pi}\sin^3(\phi)\cos^2(\theta)\,d\phi\,d\theta=\int_0^{2\pi}\cos^2(\theta)\,d\theta\,\int_0^{\pi}\sin^3(\phi)\,d\phi\\[2.5mm] &=\frac{1}{2}\int_0^{2\pi}\left(1+\cos(2\theta)\right)\,d\theta\,\int_0^{\pi}\sin(\phi)\left(1-\cos^2(\phi)\right)\,d\phi =\frac{1}{2}\bigg[\theta+\frac{1}{2}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}\,\bigg[-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\bigg]_{\phi=0}^{\pi}\\[2.5mm] &=\frac{1}{2}\cdot2\pi\cdot\frac{4}{3}=\frac{4}{3}\pi. \end{align*}

Application: physical interpretation

Suppose that \(\rho(x,y,z)\geq 0\) is a mass density function defined at the points \((x,y,z)\) of a thin sheet (say, of aluminum foil) that has the shape of a surface \(S\). Then

\[m=\iint\limits_S\rho(x,y,z)\,dS\]

denotes the (total) mass of the sheet. Furthermore, the center of mass \((\overline{x},\overline{y},\overline{z})\) is given by

\[\overline{x}=\frac{1}{m}\iint\limits_Sx\,\rho(x,y,z)\,dS,\quad\overline{y}=\frac{1}{m}\iint\limits_Sy\,\rho(x,y,z)\,dS \quad\textrm{and}\quad\overline{z}=\frac{1}{m}\iint\limits_Sz\,\rho(x,y,z)\,ds.\]

Stewart §16.7, Example 2
Evaluate \(\displaystyle\iint\limits_Sy\,dS\), where \(S\) is the surface \(z=x+y^2\) with \(0\leq x\leq 1\) and \(0\leq y\leq 2\).

Solution: Note that the surface \(S\) is the graph of a function of two variables:

\[S:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(x+y^2)\,\mathbf{k}\]

with domain \(D=[0,1]\times[0,2]=\{(x,y)\,|\,0\leq x\leq 1,\;0\leq y\leq 2\}\). Hence we have

\[\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,1\rangle\times\langle 0,1,2y\rangle=\langle -1,-2y,1\rangle\quad\Longrightarrow\quad \left|\mathbf{r}_x\times\mathbf{r}_y\right|=\sqrt{(-1)^2+(-2y)^2+1}=\sqrt{2+4y^2}\]

and therefore

\[\iint\limits_Sy\,dS=\iint\limits_Dy\sqrt{2+4y^2}\,dA=\int_0^1\,dx\,\int_0^2y\sqrt{2+4y^2}\,dy =1\cdot\bigg[\frac{1}{12}(2+4y^2)^{3/2}\bigg]_{y=0}^2=\frac{1}{12}\left(54\sqrt{2}-2\sqrt{2}\right)=\frac{13}{3}\sqrt{2}.\]

Piecewise-smooth surfaces

If \(S\) is a piecewise-smooth surface, that is, a finite union of smooth surfaces \(S_1,S_2,\ldots,S_n\) that intersect only along their boundaries, then the surface integral of \(f\) over \(S\) is defined by

\[\iint\limits_Sf(x,y,z)\,dS=\iint\limits_{S_1}f(x,y,z)\,dS+\iint\limits_{S_2}f(x,y,z)\,dS+\cdots+\iint\limits_{S_n}f(x,y,z)\,dS.\]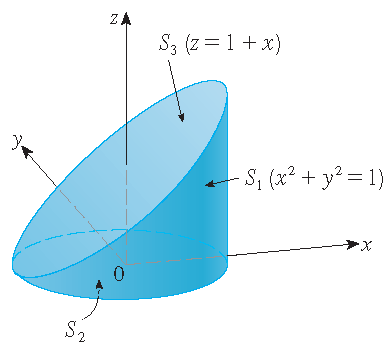

Stewart §16.7, Example 3
Evaluate \(\displaystyle\iint\limits_Sz\,dS\), where \(S\) is the surface whose sides \(S_1\) are given by the cylinder \(x^2+y^2=1\), whose bottom \(S_2\) is the disk \(x^2+y^2\leq 1\) in the plane \(z=0\) and whose top \(S_3\) is the part of the plane \(z=1+x\) that lies above \(S_2\).

Solution: The surface \(S\) is shown in the picture. For \(S_1\) we use \(\theta\) and \(z\) as parameters:

\[S_1:\;\mathbf{r}(\theta,z)=\cos(\theta)\,\mathbf{i}+\sin(\theta)\,\mathbf{j}+z\,\mathbf{k},\]

where \(0\leq\theta\leq2\pi\) and \(0\leq z\leq 1+x=1+\cos(\theta)\). Therefore

\[\mathbf{r}_{\theta}\times\mathbf{r}_z=\langle -\sin(\theta),\cos(\theta),0 \rangle\times\langle 0,0,1\rangle =\langle \cos(\theta),\sin(\theta),0 \rangle\quad\Longrightarrow\quad\left|\mathbf{r}_{\theta}\times\mathbf{r}_z\right| =\sqrt{\cos^2(\theta)+\sin^2(\theta)+0}=1.\]

Hence we have with \(D=\{(\theta,z)\,|\,0\leq\theta\leq2\pi,\;0\leq z\leq 1+\cos(\theta)\}\)

\begin{align*} \iint\limits_{S_1}z\,dS&=\iint\limits_Dz\,\left|\mathbf{r}_{\theta}\times\mathbf{r}_z\right|\,dA =\int_0^{2\pi}\int_0^{1+\cos(\theta)}z\,dz\,d\theta=\frac{1}{2}\int_0^{2\pi}\left(1+\cos(\theta)\right)^2\,d\theta\\[2.5mm] &=\frac{1}{2}\int_0^{2\pi}\left(1+2\cos(\theta)+\frac{1}{2}\left(1+\cos(2\theta)\right)\right)\,d\theta =\frac{1}{2}\bigg[\frac{3}{2}\theta+2\sin(\theta)+\frac{1}{4}\sin(2\theta)\bigg]_{\theta=0}^{2\pi}=\frac{3}{2}\pi. \end{align*}

Since \(S_2\) lies in the plane \(z=0\) we have: \(\displaystyle\iint\limits_{S_2}z\,dS=0\).

The top surface \(S_3\) lies above the unit disk \(x^2+y^2\leq 1\) and is part of the plane \(z=1+x\) which is the graph of a function of two variables:

\[S_3:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(1+x)\,\mathbf{k},\quad x^2+y^2\leq 1.\]

Then we have

\[\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,1 \rangle\times\langle 0,1,0\rangle=\langle -1,0,1\rangle\quad\Longrightarrow\quad \left|\mathbf{r}_x\times\mathbf{r}_y\right|=\sqrt{(-1)^2+0+1}=\sqrt{2}\]

and therefore, using polar coordinates, we obtain

\begin{align*} \iint\limits_{S_3}z\,dS&=\iint\limits_{x^2+y^2\leq1}(1+x)\,\left|\mathbf{r}_x\times\mathbf{r}_y\right|\,dA =\int_0^{2\pi}\int_0^1(1+r\,\cos(\theta))\,\sqrt{2}\,r\,dr\,d\theta=\sqrt{2}\int_0^{2\pi}\int_0^1\left(r+r^2\cos(\theta)\right)\,dr\,d\theta\\[2.5mm] &=\sqrt{2}\int_0^{2\pi}\bigg[\frac{1}{2}r^2+\frac{1}{3}r^3\cos(\theta)\bigg]_{r=0}^1\,d\theta =\sqrt{2}\int_0^{2\pi}\left(\frac{1}{2}+\frac{1}{3}\cos(\theta)\right)\,d\theta =\sqrt{2}\bigg[\frac{1}{2}\theta+\frac{1}{3}\sin(\theta)\bigg]_{\theta=0}^{2\pi}=\pi\sqrt{2}. \end{align*}

Finally, we conclude that

\[\iint\limits_Sz\,dS=\iint\limits_{S_1}z\,dS+\iint\limits_{S_2}z\,dS+\iint\limits_{S_3}z\,dS =\frac{3}{2}\pi+0+\pi\sqrt{2}=\left(\frac{3}{2}+\sqrt{2}\right)\pi.\]

Orientable surfaces

An orientable surface has two sides. An example of a nonorientable surface is the Möbius strip, named after the German mathematician August Ferdinand Möbius (1790-1868):

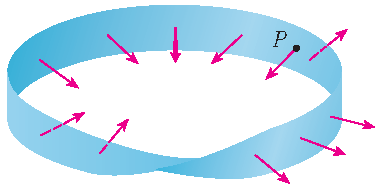
One can construct this by taking a long rectangular strip of paper,

giving it a half twist and taping the short edges together:

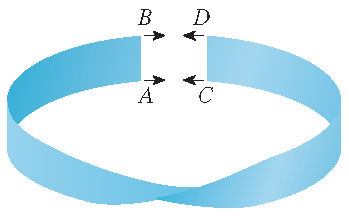
Such a Möbius strip really has only one side.

Oriented surfaces

From now on we only consider orientable (two-sided) surfaces. If it is possible to choose a unit normal vector \(\mathbf{n}\) at every point \((x,y,z)\) on such a surface such that \(\mathbf{n}\) varies continuously over \(S\), then \(S\) is called an oriented surface and the given choice of \(\mathbf{n}\) provides \(S\) with an orientation. There are two possible orientations for any orientable surface:

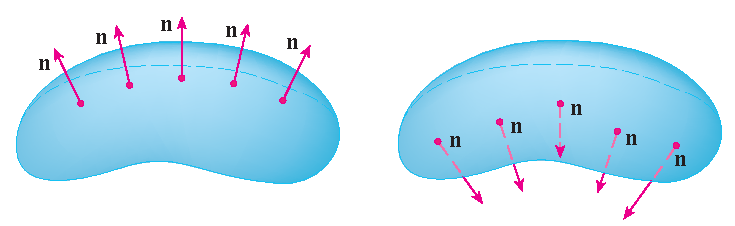
Consider an orientable parametric surface

\[S:\;\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad(u,v)\in D\]

with tangent vectors \(\mathbf{r}_u\) and \(\mathbf{r}_v\). Then the parametrization induces an orientation given by \(\displaystyle\mathbf{n}=\frac{\mathbf{r}_u\times\mathbf{r}_v}{\left|\mathbf{r}_u\times\mathbf{r}_v\right|}\) and the opposite orientation is given by \(-\mathbf{n}\).

For instance, we have seen that

\[\mathbf{r}(\phi,\theta)=a\,\sin(\phi)\,\cos(\theta)\,\mathbf{i}+a\,\sin(\phi)\,\sin(\theta)\,\mathbf{j}+a\,\cos(\phi)\,\mathbf{k}\]

with domain \(0\leq\phi\leq\pi\) and \(0\leq\theta\leq2\pi\) is a parametric representation for the sphere \(x^2+y^2+z^2=a^2\) with \(a\geq0\). Then we have

\[\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}=a\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\quad\Longrightarrow\quad \mathbf{n}=\frac{\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}}{\left|\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right|} =\frac{1}{a}\cdot\mathbf{r}(\phi,\theta).\]

Observe that \(\mathbf{n}\) points in the same direction as the position vector \(\mathbf{r}(\phi,\theta)\), that is, outward from the sphere. The opposite (inward) orientation would have been obtained if we had reversed the order of the tangent vectors beacause \(\mathbf{r}_{\theta}\times\mathbf{r}_{\phi}=-\left(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right)\).

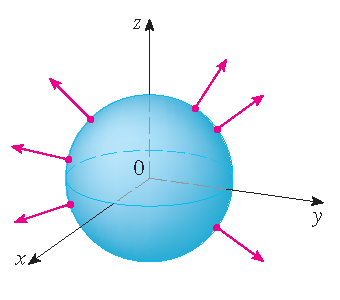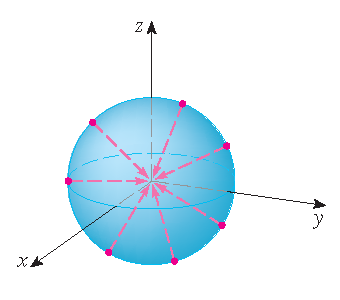positive orientation	negative orientation

For a closed surface, that is, a surface that is the boundary of a solid region \(E\), the convention is that the positive orientation is the one for which the normal vectors point outward from \(E\) and inward-pointing normals give the negative orientation.

The surface integral of a vector field

Definition: If \(\mathbf{F}\) is a continuous vector field defined on an oriented surface \(S\) with unit normal vector \(\mathbf{n}\), then

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_S\mathbf{F}\cdot\mathbf{n}\,dS\]

is the surface integral of \(\mathbf{F}\) over the surface \(S\). This integral is also called the flux of \(\mathbf{F}\) across \(S\).

The surface integral of a vector field over \(S\) is equal to the surface integral of its normal component over \(S\). If \(S\) is given by the parametrization

\[\mathbf{r}(u,v)=x(u,v)\,\mathbf{i}+y(u,v)\,\mathbf{j}+z(u,v)\,\mathbf{k},\quad(u,v)\in D\]

where \(D\) is the parameter domain, then

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_D\mathbf{F}(\mathbf{r}(u,v))\cdot\left(\mathbf{r}_u\times\mathbf{r}_v\right)\,dA,\]

since \(\mathbf{n}=\displaystyle\frac{\mathbf{r}_u\times\mathbf{r}_v}{\left|\mathbf{r}_u\times\mathbf{r}_v\right|}\) and \(dS=\left|\mathbf{r}_u\times\mathbf{r}_v\right|\,dA\).

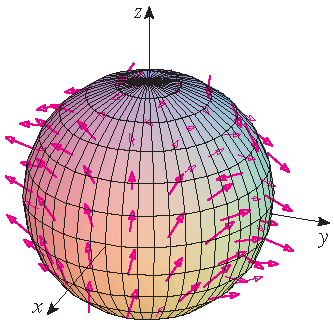
Stewart §16.7, Example 4
Find the flux of the vector field \(\mathbf{F}(x,y,z)=z\,\mathbf{i}+y\,\mathbf{j}+x\,\mathbf{k}\) across the unit sphere \(x^2+y^2+z^2=1\).

Solution: We use the parametrization

\[\mathbf{r}(\phi,\theta)=\sin(\phi)\,\cos(\theta)\,\mathbf{i}+\sin(\phi)\,\sin(\theta)\,\mathbf{j}+\cos(\phi)\,\mathbf{k}\]

with domain \(0\leq\phi\leq\pi\) and \(0\leq\theta\leq2\pi\) for the unit sphere. Then we have

\[\mathbf{r}_{\phi}\times\mathbf{\theta}=\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\]

and therefore

\begin{align*} \iint\limits_S\mathbf{F}\cdot d\mathbf{S}&=\iint\limits_D\mathbf{F}(\mathbf{r}(\phi,\theta))\cdot\left(\mathbf{r}_{\phi}\times\mathbf{r}_{\theta}\right)\,dA =\int_0^{2\pi}\int_0^{\pi}\langle\cos(\phi),\sin(\phi)\,\sin(\theta),\sin(\phi)\,\cos(\theta)\rangle\cdot\sin(\phi)\cdot\mathbf{r}(\phi,\theta)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\int_0^{\pi}\left(\sin^2(\phi)\cos(\phi)\cos(\theta)+\sin^3(\phi)\sin^2(\theta)+\sin^2(\phi)\cos(\phi)\cos(\theta)\right)\,d\phi\,d\theta\\[2.5mm] &=\int_0^{2\pi}\cos(\theta)\,d\theta\,\int_0^{\pi}2\sin^2(\phi)\cos(\phi)\,d\phi+\int_0^{2\pi}\sin^2(\theta)\,d\theta\,\int_0^{\pi}\sin^3(\phi)\,d\phi\\[2.5mm] &=\bigg[\sin(\theta)\bigg]_{\theta=0}^{2\pi}\bigg[\frac{1}{3}\sin^3(\phi)\bigg]_{\phi=0}^{\pi} +\bigg[\frac{1}{2}\theta-\frac{1}{2}\cos(2\theta)\bigg]_{\theta=0}^{2\pi}\bigg[-\cos(\phi)+\frac{1}{3}\cos^3(\phi)\bigg]_{\phi=0}^{\pi} =0+\pi\cdot\frac{4}{3}=\frac{4}{3}\pi. \end{align*}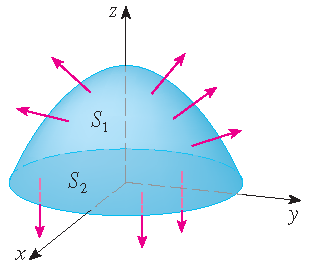

Example (compare with Stewart §16.7, Example 5)
Evaluate \(\displaystyle\iint\limits_S\mathbf{F}\cdot d\mathbf{S}\), where \(\mathbf{F}(x,y,z)=y\,\mathbf{i}+x\,\mathbf{j}+(z+1)\,\mathbf{k}\) and \(S\) is the boundary of the solid region \(E\) enclosed by the paraboloid \(z=1-x^2-y^2\) and the plane \(z=0\).

Solution: The surface \(S\) consists of a parabolic top surface \(S_1\) and a circular bottom surface \(S_2\). Since \(S\) is a closed surface, we use the convention of positive (outward) orientation. This means that \(S_1\) is oriented upward. Note that \(S_1\) is the graph of a function of two variables:

\[S_1:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+(1-x^2-y^2)\,\mathbf{k},\quad x^2+y^2\leq 1\]

with \(\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,-2x\rangle\times\langle 0,1,-2y\rangle=\langle 2x,2y,1\rangle\), which points upward. Hence we have using polar coordinates

\begin{align*} \iint\limits_{S_1}\mathbf{F}\cdot d\mathbf{S}&=\iint\limits_{x^2+y^2\leq1}\langle y,x,2-x^2-y^2\rangle\cdot\langle 2x,2y,1\rangle\,dA =\iint\limits_{x^2+y^2\leq1}\left(2xy+2xy+2-x^2-y^2\right)\,dA\\[2.5mm] &=\int_0^{2\pi}\int_0^1\left(4r^2\cos(\theta)\sin(\theta)+2-r^2\right)\,r\,dr\,d\theta =\int_0^{2\pi}\bigg[r^4\cos(\theta)\sin(\theta)+r^2-\frac{1}{4}r^4\bigg]_{r=0}^1\,d\theta\\[2.5mm] &=\int_0^{2\pi}\left(\cos(\theta)\sin(\theta)+\frac{3}{4}\right)\,d\theta =\bigg[\frac{1}{2}\sin^2(\theta)+\frac{3}{4}\theta\bigg]_{\theta=0}^{2\pi}=\frac{3}{2}\pi. \end{align*}

A parametrization of \(S_2\) is for instance

\[\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+0\,\mathbf{k},\quad x^2+y^2\leq 1\]

with \(\mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,0\rangle\times\langle 0,1,0\rangle=\langle 0,0,1\rangle\), which points upward. The positive (outward) orientation should be downward on \(S_2\), hence we have

\[\iint\limits_{S_2}\mathbf{F}\cdot d\mathbf{S}=-\iint\limits_{x^2+y^2\leq1}\langle y,x,1\rangle\cdot\langle 0,0,1\rangle\,dA =-\iint\limits_{x^2+y^2\leq1}1\,dA=-\pi.\]

We conclude that

\[\iint\limits_S\mathbf{F}\cdot d\mathbf{S}=\iint\limits_{S_1}\mathbf{F}\cdot d\mathbf{S}+\iint\limits_{S_2}\mathbf{F}\cdot d\mathbf{S} =\frac{3}{2}\pi-\pi=\frac{1}{2}\pi.\]

---

Last modified on October 18, 2021