Calculus – Vector calculus – Stokes' theorem

Stokes' theorem can be regarded as a higher-dimensional version of Green's theorem. Whereas Green's theorem relates a double integral over a plane region \(D\) to a line integral around its plane boundary curve of \(D\), Stokes' theorem relates a surface integral over a surface \(S\) to a line integral around the boundary (space) curve of \(S\).

Orientation

Consider an oriented surface \(S\) with unit normal vector \(\mathbf{n}\).

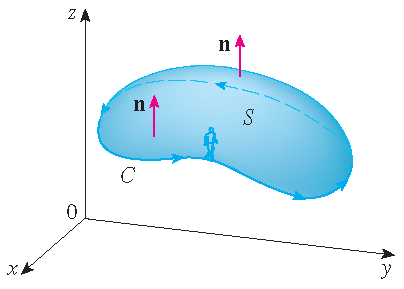
The orientation of \(S\) induces the positive orientation of the boundary curve \(\mathcal{C}\).

Theorem: Let \(S\) be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve \(\mathcal{C}\) with positive orientation. Let \(\mathbf{F}\) be a vector field whose components have continuous partial derivatives on an open region in \(\mathbb{R}^3\) that contains \(S\). Then

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\iint\limits_S\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}.\]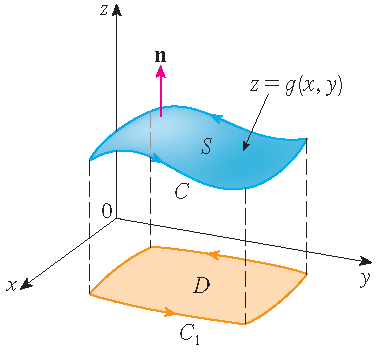

Proof (only for the graph of a function): We assume that \(S\) is the graph of a function \(g(x,y)\) with domain \(D\), where \(g\) has continuous second-order partial derivatives and \(D\) is a regular plane region whose boundary curve \(\mathcal{C}_1\) corresponds to \(\mathcal{C}\). If the orientation of \(S\) is upward, then the positive orientation of \(\mathcal{C}\) corresponds to the positive orientation of \(\mathcal{C}_1\). We are also given that \(\mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j}+R\,\mathbf{k}\), where the partial derivatives of \(P\), \(Q\) and \(R\) are continuous. Since

\[\textrm{curl}\,\mathbf{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\,\mathbf{i} +\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\,\mathbf{j} +\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,\mathbf{k}\]

and

\[S:\;\mathbf{r}(x,y)=x\,\mathbf{i}+y\,\mathbf{j}+g(x,y)\,\mathbf{k}\quad\Longrightarrow\quad \mathbf{r}_x\times\mathbf{r}_y=\langle 1,0,\frac{\partial g}{\partial x}\rangle\times\langle 0,1,\frac{\partial g}{\partial y}\rangle =\langle-\frac{\partial g}{\partial x},-\frac{\partial g}{\partial y},1\rangle,\]

we have (note that this normal vector points upward)

\[\iint\limits_S\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S} =\iint\limits_D\left(-\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\frac{\partial z}{\partial x} -\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\frac{\partial z}{\partial y} +\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA,\]

where the partial derivatives of \(P\), \(Q\) and \(R\) are evaluated at \((x,y,g(x,y))\).

If \(\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}\) with \(a\leq t\leq b\) is a parametrization of \(\mathcal{C}_1\), then a parametric representation of \(\mathcal{C}\) is

\[\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}+g(x(t),y(t))\,\mathbf{k},\quad a\leq t\leq b.\]

Hence we have using the chain rule and Green's theorem

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_a^b\left(P\frac{dx}{dt}+Q\frac{dy}{dt}+R\frac{dz}{dt}\right)\,dt =\int_a^b\left(P\,\frac{dx}{dt}+Q\,\frac{dy}{dt}+R\,\left(\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}\right)\right)\,dt\\[2.5mm] &=\int_a^b\left(\left(P+R\frac{\partial z}{\partial x}\right)\frac{dx}{dt}+\left(Q+R\frac{\partial z}{\partial y}\right)\frac{dy}{dt}\right)\,dt =\int\limits_{\mathcal{C}_1}\left(P+R\,\frac{\partial z}{\partial x}\right)\,dx+\left(Q+R\,\frac{\partial z}{\partial y}\right)\,dy\\[2.5mm] &=\iint\limits_D\left(\frac{\partial}{\partial x}\left(Q+R\frac{\partial z}{\partial y}\right) -\frac{\partial}{\partial y}\left(P+R\frac{\partial z}{\partial x}\right)\right)\,dA. \end{align*}

Note that \(P\), \(Q\) and \(R\) are functions of \(x\), \(y\) and \(z\) and that \(z=g(x,y)\) is itself a function of \(x\) and \(y\). Hence, using the chain rule, we obtain

\[\frac{\partial}{\partial x}\left(Q+R\,\frac{\partial z}{\partial y}\right) =\frac{\partial Q}{\partial x}+\frac{\partial Q}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial R}{\partial x}\frac{\partial z}{\partial y} +\frac{\partial R}{\partial z}\frac{\partial z}{\partial x}\frac{\partial z}{\partial y}+R\frac{\partial^2z}{\partial x\,\partial y}\]

and

\[\frac{\partial}{\partial y}\left(P+R\,\frac{\partial z}{\partial x}\right) =\frac{\partial P}{\partial y}+\frac{\partial P}{\partial z}\frac{\partial z}{\partial y}+\frac{\partial R}{\partial y}\frac{\partial z}{\partial x} +\frac{\partial R}{\partial z}\frac{\partial z}{\partial y}\frac{\partial z}{\partial x}+R\frac{\partial^2z}{\partial y\,\partial x}.\]

Hence, using Clairaut's theorem, we obtain

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\iint\limits_D\left(-\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\frac{\partial z}{\partial x} -\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\frac{\partial z}{\partial y} +\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dA.\]

This completes the proof.

Stewart §16.8, Example 1
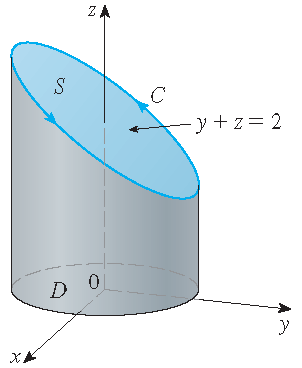
Evaluate \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), where \(\mathbf{F}(x,y,z)=-y^2\,\mathbf{i}+x\,\mathbf{j}+z^2\,\mathbf{k}\) and \(\mathcal{C}\) is the curve of intersection of the plane \(y+z=2\) and the cylinder \(x^2+y^2=1\) which is traversed counterclockwise when viewed from above.

Solution: The curve \(\mathcal{C}\) is the ellipse shown in the picture. A parametrization is

\[\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+\left(2-\sin(t)\right)\,\mathbf{k},\quad 0\leq t\leq 2\pi.\]

So a direct evaluation would be

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\int_0^{2\pi}\langle -\sin^2(t),\cos(t),\left(2-\sin(t)\right)^2\rangle\cdot \langle -\sin(t),\cos(t),-\cos(t)\rangle\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\sin^3(t)+\cos^2(t)-\cos(t)\left(2-\sin(t)\right)^2\right)\,dt\\[2.5mm] &=\int_0^{2\pi}\left(\sin(t)\left(1-\cos^2(t)\right)+\frac{1}{2}+\frac{1}{2}\cos(2t)-\cos(t)\left(2-\sin(t)\right)^2\right)\,dt\\[2.5mm] &=\bigg[-\cos(t)+\frac{1}{3}\cos^3(t)+\frac{1}{2}t+\frac{1}{4}\sin(2t)+\frac{1}{3}\left(2-\sin(t)\right)^3\bigg]_{t=0}^{2\pi}=\pi. \end{align*}

Using

\[\textrm{curl}\,\mathbf{F}=(0-0)\,\mathbf{i}+(0-0)\,\mathbf{j}+(1+2y)\,\mathbf{k}=(1+2y)\,\mathbf{k}\]

Stokes' theorem implies, using polar coordinates, that

\begin{align*} \int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}&=\iint\limits_S\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S} =\iint\limits_D(1+2y)\,dA=\int_0^{2\pi}\int_0^1\left(1+2r\sin(\theta)\right)\,r\,dr\,d\theta =\int_0^{2\pi}\bigg[\frac{1}{2}r^2+\frac{2}{3}r^3\sin(\theta)\bigg]_{r=0}^1\,d\theta\\[2.5mm] &=\int_0^{2\pi}\left(\frac{1}{2}+\frac{2}{3}\sin(\theta)\right)\,d\theta =\bigg[\frac{1}{2}\theta-\frac{2}{3}\cos(\theta)\bigg]_{\theta=0}^{2\pi}=\pi. \end{align*}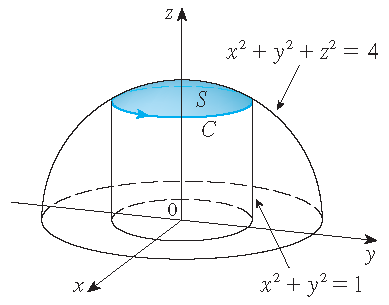

Stewart §16.8, Example 2
Use Stokes' theorem to evaluate the integral \(\displaystyle\iint\limits_S\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}\), where \(\mathbf{F}(x,y,z)=xz\,\mathbf{i}+yz\,\mathbf{j}+xy\,\mathbf{k}\) and \(S\) is the part of the sphere \(x^2+y^2+z^2=4\) that lies inside the cylinder \(x^2+y^2=1\) and above the \(xy\)-plane.

Solution: To find the boundary curve \(\mathcal{C}\) we solve the equations \(x^2+y^2+z^2=4\) and \(x^2+y^2=1\). Subtracting, we get \(z^2=3\) and so \(z=\sqrt{3}\) (since \(z>0\)). Hence \(\mathcal{C}\) is the circle given by \(x^2+y^2=1\) and \(z=\sqrt{3}\). So, a parametrization of \(\mathcal{C}\) is

\[\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}+\sqrt{3}\,\mathbf{k},\quad 0\leq t\leq 2\pi.\]

Hence, Stokes' theorem implies that

\begin{align*} \iint\limits_S\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}&=\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\int_0^{2\pi}\mathbf{F}(\mathbf{r}(t))\cdot\mathbf{r}'(t)\,dt =\int_0^{2\pi}\langle \sqrt{3}\cos(t),\sqrt{3}\sin(t),\cos(t)\sin(t)\rangle\cdot\langle -\sin(t),\cos(t),0\rangle\,dt\\[2.5mm] &=\int_0^{2\pi}\left(-\sqrt{3}\sin(t)\cos(t)+\sqrt{3}\sin(t)\cos(t)+0\right)\,dt=0. \end{align*}

Example: compare with Stewart §16.8, Exercise 1
Let \(H\) be the hemisphere \(x^2+y^2+z^2=4\) with \(z\geq 0\) and \(P\) the part of the paraboloid \(z=4-x^2-y^2\) with \(z\geq 0\). If \(\mathbf{F}\) is a vector field on \(\mathbb{R}^3\) whose components have continuous partial derivatives, then show that

\[\iint\limits_H\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}=\iint\limits_P\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}.\]

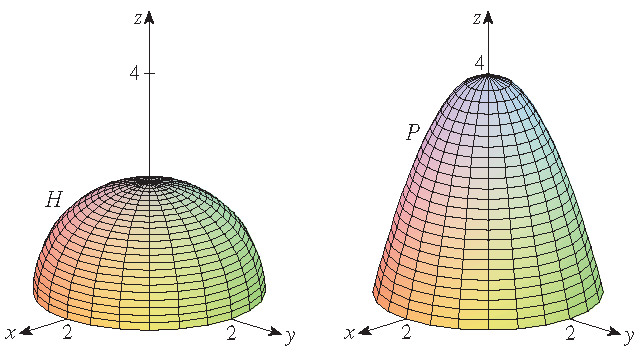
Solution: Note that the circle \(\mathcal{C}\) given by \(x^2+y^2=4\) and \(z=0\) is the boundary curve of both the surfaces \(H\) and \(P\). Taking the orientation induced by that of both surfaces, Stokes' theorem implies that

\[\iint\limits_H\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}=\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r} =\iint\limits_P\textrm{curl}\,\mathbf{F}\cdot d\mathbf{S}.\]

---

Last modified on October 19, 2021