Analyse – Vectoranalyse – De hoofdstelling voor lijnintegralen

Stelling: Laat \(\mathcal{C}\) een gladde kromme zijn gegeven door de vectorfunctie \(\mathbf{r}(t)\) met \(a\leq t\leq b\). Laat \(f\) een differentieerbare functie zijn van twee of drie variabelen waarvan de gradiëntvector \(\nabla f\) continu is op \(\mathcal{C}\). Dan is

\[\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r}=f(\mathbf{r}(b))-f(\mathbf{r}(a)).\]

Bewijs: Merk op dat geldt

\[\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r}=\int_a^b\nabla f(\mathbf{r}(t))\cdot \mathbf{r}'(t)\,dt =\int_a^b\left(\frac{\partial f}{\partial x}\cdot\frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot\frac{dy}{dt}+\frac{\partial f}{\partial z}\cdot\frac{dz}{dt}\right)\,dt =\int_a^b\frac{d}{dt}f(\mathbf{r}(t))\,dt=f(\mathbf{r}(b))-f(\mathbf{r}(a)).\]

Padonafhankelijkheid

Definitie: Als \(\mathbf{F}\) een continu vectorveld is met domein \(D\), dan heet de lijnintegraal \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) padonafhankelijk als

\[\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\]

voor elk tweetal paden \(\mathcal{C}_1\) en \(\mathcal{C}_2\) in \(D\) die dezelfde begin- en eindpunten hebben.

Definitie: Een kromme \(\mathcal{C}\) met parametrisering \(\mathbf{r}(t)\) en \(a\leq t\leq b\) heet gesloten als het eindpunt samenvalt met het beginpunt, dat wil zeggen, als \(\mathbf{r}(b)=\mathbf{r}(a)\).

Stelling: De lijnintegraal \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) is padonafhankelijk in \(D\) dan en slechts dan als \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) voor elke gesloten kromme \(\mathcal{C}\) in \(D\).

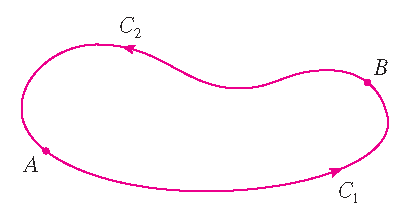Bewijs: Als \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) padonafhankelijk is in \(D\) en \(\mathcal{C}\) is een willekeurige kromme in \(D\), dan kunnen we twee willekeurige punten \(A\) en \(B\) op \(\mathcal{C}\) kiezen en de kromme \(\mathcal{C}\) zien als samengesteld uit de kromme \(\mathcal{C}_1\) van \(A\) tot \(B\) gevolgd door de kromme \(\mathcal{C}_2\) van \(B\) tot \(A\). Dan geldt:

\[\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} +\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} -\int\limits_{-\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=0\]

omdat \(\mathcal{C}_1\) and \(-\mathcal{C}_2\) hetzelfde begin- en eindpunt hebben.

Omgekeerd, als \(\displaystyle\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=0\) voor elke gesloten kromme \(\mathcal{C}\) in \(D\), dan volgt de padonafhankelijkheid als volgt. Neem twee krommen \(\mathcal{C}_1\) en \(\mathcal{C}_2\) van \(A\) tot \(B\) in \(D\) en definieer \(\mathcal{C}\) als de kromme bestaande uit \(\mathcal{C}_1\) gevolgd door \(-\mathcal{C}_2\). Dan geldt

\[0=\oint\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} +\int\limits_{-\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r} -\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\]

en dus \(\displaystyle\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\), waaruit volgt dat \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) padonafhankelijk is in \(D\).

Definitie: Een gebied \(D\) heet open als voor elk punt \(P\) in \(D\) er een cirkelschijf met middelpunt \(P\) (en positieve straal) bestaat die geheel in \(D\) ligt.

Opmerking: Dus: \(D\) bevat geen van z'n randpunten.

Definitie: Een gebied \(D\) heet samenhangend als elk tweetal punten in \(D\) verbonden kan worden door een kromme die in \(D\) ligt.

Stelling: Neem aan dat \(\mathbf{F}\) een vectorveld is dat continu is op een open samenhangend gebied \(D\). Als \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) padonafhankelijk is in \(D\), dan is \(\mathbf{F}\) een conservatief vectorveld op \(D\), dat wil zeggen, er bestaat een (potentiaal)functie \(f\) zodat \(\mathbf{F}=\nabla f\).

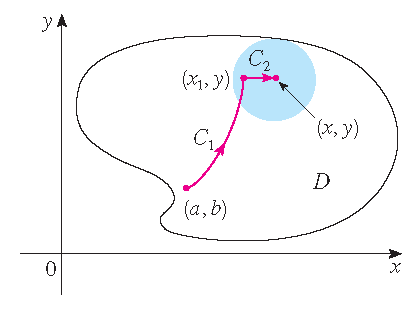Bewijs: Laat \((a,b)\) een vast punt zijn in \(D\). We construeren dan de gewenste potentiaalfunctie \(f\) door het definiëren van \(f(x,y)=\displaystyle\int_{(a,b)}^{(x,y)}\mathbf{F}\cdot d\mathbf{r}\) voor elk punt \((x,y)\) in \(D\). Omdat \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) padonafhankleijk is, maakt het niet uit welk pad \(\mathcal{C}\) we kiezen van \((a,b)\) tot \((x,y)\) om \(f(x,y)\) te berekenen. Omdat \(D\) open is, bestaat er een cirkelschijf in \(D\) met middelpunt \((x,y)\). Kies een punt \((x_1,y)\) in die cirkelschijf met \(x_1 < x\) en laat \(\mathcal{C}\) bestaan uit een willekeurig pad \(\mathcal{C}_1\) van \((a,b)\) tot \((x_1,y)\) gevolgd door het horizontale lijnstuk \(\mathcal{C}_2\) van \((x_1,y)\) tot \((x,y)\). Dan geldt

\[f(x,y)=\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}+\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r} =\int_{(a,b)}^{(x_1,y)}\mathbf{F}\cdot d\mathbf{r}+\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}.\]

Merk op dat de eerste integraal niet van \(x\) afhangt, dus: \(\displaystyle\frac{\partial}{\partial x}f(x,y)=0+\frac{\partial}{\partial x}\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\). Laat \(\mathbf{F}=\langle P,Q \rangle\), dan is \(\displaystyle\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r} =\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy\). Op \(\mathcal{C}_2\) is \(y\) constant, dus \(dy=0\). Met \(t\) als de parameter, waarbij \(x_1\leq t\leq x\), volgt

\[\frac{\partial}{\partial x}f(x,y)=\frac{\partial}{\partial x}\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy =\frac{\partial}{\partial x}\int_{x_1}^xP(t,y)\,dt=P(x,y).\]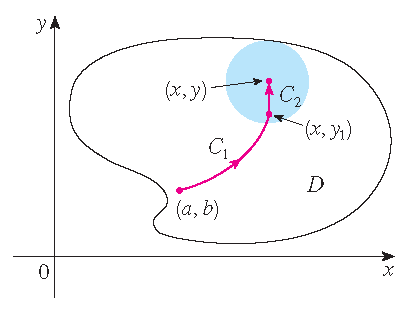

Evenzo kunnen we een punt \((x,y_1)\) in de cirkelschijf kiezen met \(y_1 < y\) en laat dan \(\mathcal{C}\) bestaan uit een willekeurig pad \(\mathcal{C}_1\) van \((a,b)\) tot \((x,y_1)\) gevolgd door het verticale lijnstuk \(\mathcal{C}_2\) van \((x,y_1)\) tot \((x,y)\). Dan geldt

\[\frac{\partial}{\partial y}f(x,y)=\frac{\partial}{\partial y}\int\limits_{\mathcal{C}_2}P\,dx+Q\,dy =\frac{\partial}{\partial y}\int_{y_1}^yQ(x,t)\,dt=Q(x,y).\]

Dus geldt: \(\mathbf{F}=\langle P,Q \rangle =\displaystyle\frac{\partial f}{\partial x}\,\mathbf{i}+\frac{\partial f}{\partial y}\,\mathbf{j}=\nabla f\), waaruit volgt dat \(\mathbf{F}\) conservatief is.

Conservatieve vectorvelden

Stelling: Als \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) een conservatief vectorveld is, waarbij \(P\) en \(Q\) continue eerste-orde partiële afgeleiden hebben op een domein \(D\), dan geldt overal in \(D\) dat \[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.\]

Bewijs: Omdat \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) een conservatief vectorveld is, bestaat er een (potentiaal)functie \(f\) zodat \(\mathbf{F}=\nabla f\) waaruit volgt dat \(P=\displaystyle\frac{\partial f}{\partial x}\) en \(Q=\displaystyle\frac{\partial f}{\partial y}\). Met behulp van de stelling van Clairaut volgt dan:

\[\frac{\partial P}{\partial y}=\frac{\partial^2f}{\partial y\,\partial x}=\frac{\partial^2f}{\partial x\,\partial y}=\frac{\partial Q}{\partial x}.\]

Stewart §16.3, Voorbeeld 3 en Voorbeeld 4
Bereken \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\), waarbij \(\mathbf{F}(x,y)=(3+2xy)\,\mathbf{i}+(x^2-3y^2)\,\mathbf{j}\) en \(\mathcal{C}\) is de kromme gegeven door \(\mathbf{r}(t)=e^t\sin(t)\,\mathbf{i}+e^t\cos(t)\,\mathbf{j}\) met \(0\leq t\leq\pi\).

Oplossing: Merk op dat \(\mathbf{F}=\langle P,Q \rangle\) met \(P(x,y)=3+2xy\) en \(Q(x,y)=x^2-3y^2\). Dan geldt: \(\displaystyle\frac{\partial P}{\partial y}=2x=\frac{\partial Q}{\partial x}\), waaruit volgt dat \(\mathbf{F}\) conservatief is. Dus: er bestaa een (potentiaal)functie \(f\) zodat \(\mathbf{F}=\nabla f\):

\[f_x(x,y)=3+2xy\quad\Longrightarrow\quad f(x,y)=3x+x^2y+g(y),\] waaruit volgt dat \(f_y(x,y)=x^2+g'(y)\) en dat is gelijk aan \(Q(x,y)=x^2-3y^2\) als \(g'(y)=-3y^2\). Dus: \(g(y)=-y^3+K\) voor zekere constante \(K\). Dus: \(f(x,y)=3x+x^2y-y^3+K\) is een potentiaalfunctie voor iedere constante \(K\).

Omdat \(\mathbf{r}(0)=(0,1)\) en \(\mathbf{r}(\pi)=(0,-e^{\pi})\), volgt dat

\[\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}=\int\limits_{\mathcal{C}}\nabla f\cdot d\mathbf{r} =f(\mathbf{r}(\pi))-f(\mathbf{r}(0))=f(0,-e^{\pi})-f(0,1)=e^{3\pi}-(-1)=e^{3\pi}+1.\]

Definitie: Een kromme \(\mathcal{C}\) heet enkelvoudig als deze zichzelf nergens snijdt.

enkelvoudig, niet gesloten	niet enkelvoudig, niet gesloten	enkelvoudig, gesloten	niet enkelvoudig, gesloten

Definitie: Een gebied \(D\) heet enkelvoudig samenhangend als het samenhangend is zodat elke enkelvoudig gesloten kromme in \(D\) alleen punten in \(D\) omsluit.

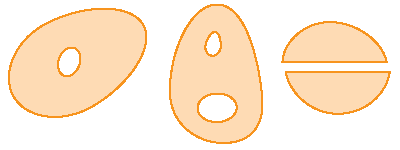enkelvoudig samenhangend	niet enkelvoudig samenhangend

Stelling: Laat \(\mathbf{F}(x,y)=P(x,y)\,\mathbf{i}+Q(x,y)\,\mathbf{j}\) een vectorveld zijn op een open enkelvoudig samenhangend gebied \(D\). Neem aan dat \(P\) en \(Q\) continue eerste-orde partiële afgeleiden hebben en

\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\quad\textrm{overal op}\quad D.\]

Dan is \(\mathbf{F}\) conservatief.

Bewijs: Dit is een gevolg van de stelling van Green en zal later worden bewezen.

Stewart §16.3, Opgave 35
Laat \(\mathbf{F}(x,y)=\displaystyle-\frac{y}{x^2+y^2}\,\mathbf{i}+\frac{x}{x^2+y^2}\,\mathbf{j}\). Toon aan dat \(\displaystyle\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\) en laat zien dat \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) niet padonafhankelijk is.

Oplossing: Laat \(P(x,y)=-\displaystyle\frac{y}{x^2+y^2}\) en \(Q(x,y)=\displaystyle\frac{x}{x^2+y^2}\), dan volgt:

\[\frac{\partial P}{\partial y}=\frac{-(x^2+y^2)+2y^2}{(x^2+y^2)^2}=\frac{y^2-x^2}{(x^2+y^2)^2}\quad\textrm{and}\quad \frac{\partial Q}{\partial x}=\frac{x^2+y^2-2-x^2}{(x^2+y^2)^2}=\frac{y^2-x^2}{(x^2+y^2)^2}.\]

Merk op dat dit geldt op het domein \(\mathbb{R}^2\setminus\{(0,0)\}\), hetgeen niet enkelvoudig samenhangend is vanwege de perforatie. Hieruit volgt dat de stelling niet kan worden toegepast.

Laat \(\mathcal{C}_1\) de bovenste helft zijn van de eenheidscirkel \(x^2+y^2=1\) van \((1,0)\) tot \((-1,0)\) met parametrisering \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+\sin(t)\,\mathbf{j}\) en \(0\leq t\leq\pi\). Dan geldt

\[\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}=\int_0^{\pi}\langle -\sin(t),\cos(t) \rangle\cdot\langle -\sin(t),\cos(t) \rangle\,dt =\int_0^{\pi}(\sin^2(t)+\cos^2(t))\,dt=\int_0^{\pi}dt=\pi.\]

Echter, laat \(\mathcal{C}_2\) de onderste helft zijn van de eenheidscirkel \(x^2+y^2=1\) van \((1,0)\) tot \((-1,0)\) met parametrisering \(\mathbf{r}(t)=\cos(t)\,\mathbf{i}+-\sin(t)\,\mathbf{j}\) en \(0\leq t\leq\pi\). Dan geldt

\[\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}=\int_0^{\pi}\langle \sin(t),\cos(t) \rangle\cdot\langle -\sin(t),-\cos(t) \rangle\,dt =\int_0^{\pi}(-\sin^2(t)-\cos^2(t))\,dt=-\int_0^{\pi}dt=-\pi.\]

Dus: \(\displaystyle\int\limits_{\mathcal{C}_1}\mathbf{F}\cdot d\mathbf{r}\neq\int\limits_{\mathcal{C}_2}\mathbf{F}\cdot d\mathbf{r}\), waaruit volgt dat \(\displaystyle\int\limits_{\mathcal{C}}\mathbf{F}\cdot d\mathbf{r}\) niet padonafhnakelijk is.

---

Laatst gewijzigd op 11 oktober 2021