Lineaire Algebra – Stelsels lineaire vergelijkingen – Toepassingen 2
Elektrische stroom in een eenvoudig elektrisch netwerk kan worden beschreven door een stelsel lineaire vergelijkingen. Een spanningsbron zoals een accu/batterij forceert een stroom van elektronen door het netwerk. Als de stroom door een weerstand gaat, dan wordt een deel van de spanning "verbruikt"; volgens de wet van Ohm wordt deze "spanningsval" door een weerstand gegeven door \(V=RI\), waarbij de spanning \(V\) wordt gemeten in volt, de weerstand \(R\) in ohm (weergegeven door \(\Omega\)) en de stroom \(I\) in ampère.
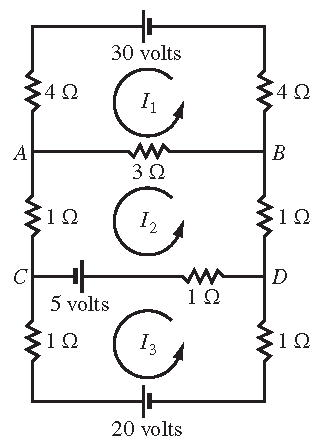
Het netwerk in het plaatje bestaat uit drie lussen. De stroom door de drie lussen wordt genoteerd door \(I_1\), \(I_2\) en \(I_3\). De aangegeven
richtingen zijn willekeurig; als blijkt dat een stroom negatief is, dan is de werkelijke richting tegengesteld aan de gekozen richting in het plaatje.
Als de richting van de stroom van de positieve (langere) kant van een accu/batterij naar de negatieve (kortere) kant stroomt, dan is de
spanning positief; anders is de spanning negatief.
De stroom in een lus wordt bepaald door de volgende regel:
Spanningswet van Kirchhoff
De som van de \(RI\) spanningsverschillen in één richting in een lus is gelijk aan de som van de spanningsbronnen in
dezelfde richting in die lus.
Nu kunnen we de lusstromen in het netwerk van het plaatje bepalen:
In de eerste lus gaat de stroom \(I_1\) door drie weerstanden, en de som van de \(RI\) spanningsverschillen is gelijk aan \(4I_1+4I_1+3I_1=11I_1\). Er gaat ook stroom van de tweede lus door een deel van de eerste lus, namelijk door de tak tussen \(A\) en \(B\). De bijbehorende spanningsval \(RI\) is daar \(3I_2\) volt. Echter, de richting van de stroom door de tak \(AB\) in de eerste lus is tegengesteld aan de richting van de stroom gekozen in de tweede lus, dus de som van alle \(RI\) spanningsverschillen in de eerste lus is \(11I_1-3I_2\). Omdat de spanning in de eerste lus \(30\) volt is, volgt uit de spanningswet van Kirchhoff dat \(11I_1-3I_2=30\).
De vergelijking voor de tweede lus is: \(-3I_1+6I_2-I_3=5\). De term \(-3I_1\) komt van de stroom in de eerste lus door de tak \(AB\) met een negatief spanningsverschil omdat de richting van de stroom tegengesteld is aan die in de tweede lus. De term \(6I_2\) is de som van alle weerstanden in de tweede lus vermenigvuldigd met de lusstroom. De term \(-I_3\) komt van de stroom in de derde lus die door de weerstand van \(1\) ohm stroomt in de tak \(CD\), in de richting tegengesteld aan de lusstroom in de tweede lus.
De vergelijking voor de derde lus is: \(-I_2+3I_3=-25\). Merk op dat de \(5\)-volts batterij in de tak \(CD\) wordt meegeteld als een deel van zowel de tweede als de derde lus, maar dat geeft \(-5\) volt voor de derde lus omdat de richting tegengesteld is aan die gekozen in de derde lus. De \(20\)-volts batterij is ook negatief om dezelfde reden.
Dus geldt:
\[\left\{\begin{array}{rrrcr}11I_1&-3I_2&&=&30\\-3I_1&+6I_2&-I_3&=&5\\&-I_2&+3I_3&=&-25\end{array}\right.\quad\Longrightarrow\quad \left(\left.\begin{matrix}11&-3&0\\-3&6&-1\\0&-1&3\end{matrix}\,\right|\,\begin{matrix}30\\5\\-25\end{matrix}\right)\sim\;\cdots\;\sim \left(\left.\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}\,\right|\,\begin{matrix}3\\1\\-8\end{matrix}\right).\]De negatieve waarde van \(I_3\) geeft aan de werkelijke richting van de stroom in de derde lus tegengesteld is aan de richting die gekozen is in het plaatje.
Het is instructief om het stelsel als een vectorvergelijking te bekijken: \(I_1\begin{pmatrix}11\\-3\\0\end{pmatrix}+I_2\begin{pmatrix}-3\\6\\-1\end{pmatrix} +I_3\begin{pmatrix}0\\-1\\3\end{pmatrix}=\begin{pmatrix}30\\5\\-25\end{pmatrix}\). Merk op dat de vectoren aan de linkerkant de weerstanden in de drie lussen weergeven; een weerstand worden negatief genoteerd als de richting van de bijbehorende stroom tegengesteld is aan die van de bijbehorende lus. De vector aan de rechterkant geeft de spanning in de drie lussen weer. Definieer nu
\[R_1=\begin{pmatrix}11\\-3\\0\end{pmatrix},\quad R_2=\begin{pmatrix}-3\\6\\-1\end{pmatrix},\quad R_3=\begin{pmatrix}0\\-1\\3\end{pmatrix} \quad\text{en}\quad V=\begin{pmatrix}30\\5\\-25\end{pmatrix},\]dan herkennen we de wet van Ohm in de matrixvergelijking \(RI=V\), waarbij \(R=\Bigg(R_1\;R_2\;R_3\Bigg)\) en \(I=\begin{pmatrix}I_1\\I_2\\I_3\end{pmatrix}\).
Differentievergelijkingen
Als \(A\) een vierkante matrix is, dan heet \(\mathbf{x}_{k+1}=A\mathbf{x}\) voor \(k=0,1,2,\ldots\) een lineaire differentievergelijking of recurrente betrekking. Gegeven zo'n vergelijking of betrekking kan men \(\mathbf{x}_1\), \(\mathbf{x}_2\), enzovoort berekenen op voorwaarde dat \(\mathbf{x}_0\) bekend is.
Migratie
Een onderwerp van belang voor demografen is de beweging van populaties of groepen mensen van de ene regio naar een andere. Het model dat we hier bekijken bestudeert de wijzigingen in de populatie van het centrum en de buitenwijken van een bepaalde stad over een periode van een aantal jaren. Beginnend in een bepaald jaar is de beginpopulatievector \(\mathbf{x}_0=\begin{pmatrix}r_0\\s_0\end{pmatrix}\), waarbij \(r_0\) de populatie van het centrum en \(s_0\) de populatie van de buitenwijken aangeeft in dat eerste jaar. Voor de volgende jaren worden de populaties weergegeven door de vectoren \(\mathbf{x}_1=\begin{pmatrix}r_1\\s_1\end{pmatrix}\), \(\mathbf{x}_2=\begin{pmatrix}r_2\\s_2\end{pmatrix}\), enzovoort. Ons doel is nu om wiskundig te beschrijven hoe deze vectoren met elkaar samenhangen.
Neem aan dat demografische studies hebben aangetoond dat jaarlijks ongeveer \(6\%\) van de populatie in het centrum verhuist naar de buitenwijken, terwijl \(4\%\) van de populatie van de buitenwijken verhuist naar het centrum. Hieruit volgt dat \(94\%\) van de populatie in het centrum in de stad blijft en dat \(96\%\) van de populatie van de buitenwijken daar blijft. Na één jaar wordt het oorspronkelijke aantal van \(r_0\) personen in het centrum verdeeld over het centrum en de buitenwijken als \(\begin{pmatrix}0.94r_0\\0.06r_0\end{pmatrix}=r_0\begin{pmatrix}0.94\\0.06\end{pmatrix}\). Het oorspronkelijke aantal van \(s_0\) personen in de buitenwijken wordt verdeeld als \(s_0\begin{pmatrix}0.04\\0.96\end{pmatrix}\). Dus geldt:
\[\begin{pmatrix}r_1\\s_1\end{pmatrix}=r_0\begin{pmatrix}0.94\\0.06\end{pmatrix}+s_0\begin{pmatrix}0.04\\0.96\end{pmatrix} =\begin{pmatrix}0.94&0.04\\0.06&0.96\end{pmatrix}\begin{pmatrix}r_0\\s_0\end{pmatrix}.\]Aannemend dat dit patroon zich blijft herhalen, geeft dit de differentievergelijking \(\mathbf{x}_{k+1}=M\mathbf{x}_k\) voor \(k=0,1,2,\ldots\), waarbij \(M=\begin{pmatrix}0.94&0.04\\0.06&0.96\end{pmatrix}\) de migratiematrix heet. Beginnend met \(\mathbf{x}_0=\begin{pmatrix}60000\\40000\end{pmatrix}\) volgt dan: \(\mathbf{x}_1=M\mathbf{x}_0 =\begin{pmatrix}0.94&0.04\\0.06&0.96\end{pmatrix}\begin{pmatrix}60000\\40000\end{pmatrix}=\begin{pmatrix}58000\\42000\end{pmatrix}\),
\[\mathbf{x}_2=M\mathbf{x}_1=\begin{pmatrix}0.94&0.04\\0.06&0.96\end{pmatrix}\begin{pmatrix}58000\\42000\end{pmatrix} =\begin{pmatrix}56200\\43800\end{pmatrix},\quad\mathbf{x}_3=M\mathbf{x}_2=\begin{pmatrix}0.94&0.04\\0.06&0.96\end{pmatrix} \begin{pmatrix}56200\\43800\end{pmatrix}=\begin{pmatrix}54580\\45420\end{pmatrix},\quad\ldots.\]Autoverhuurbedrijf
Een ander voorbeeld is een autoverhuurbedrijf met drie vestigingen; eentje bij de luchthaven, eentje in de binnenstad en eentje in een buitenwijk. De policy is dat een gehuurd voertuig teruggebracht mag worden bij een vestiging naar keuze. Onderzoek heeft uitgewezen dat van de auto's die bij het vliegveld worden gehuurd, \(10\%\) wordt ingeleverd in het centrum en \(5\%\) in de buitenwijk. Van de auto's gehuurd bij de vestiging in het centrum wordt \(10\%\) ingeleverd bij de luchthaven en \(5\%\) in de buitenwijk. Van de auto's gehuurd in de buitenwijk wordt \(15\%\) teruggebracht bij het vliegveld en \(5\%\) in de binnenstad. We gaan er van uit dat het totale wagenpark gelijk blijft.
We kiezen nu vectoren met drie kentallen in de volgorde: luchthaven, binnenstad en buitenwijk. Dan volgt: \(\mathbf{x}_{k+1}=A\mathbf{x}_k\) voor \(k=0,1,2,\ldots\) met
\[A=\begin{pmatrix}0.85&0.15&0.15\\0.10&0.80&0.05\\0.05&0.05&0.80\end{pmatrix}.\]Iedere stap zou dan een dag of een week kunnen zijn. Gegeven een bepaalde verdeling van de voertuigen over de drie vestigingen, kunnen we vervolgens de verschuivingen berekenen. Stel dat het wagenpark van het bedrijf uit \(100\) auto's bestaat en dat deze ala volgt worden verdeeld over de drie vestigingen: \(40\) bij het vliegveld, \(30\) in het centrum en \(30\) in de buitenwijk. Dan ziet het verloop er zo uit:
\[\mathbf{x}_0=\begin{pmatrix}40\\30\\30\end{pmatrix},\quad\mathbf{x}_1=A\mathbf{x}_0=\begin{pmatrix}0.85&0.15&0.15\\0.10&0.80&0.05\\0.05&0.05&0.80\end{pmatrix} \begin{pmatrix}40\\30\\30\end{pmatrix}=\begin{pmatrix}43.0\\29.5\\27.5\end{pmatrix},\quad\mathbf{x}_2=A\mathbf{x}_1 =\begin{pmatrix}0.85&0.15&0.15\\0.10&0.80&0.05\\0.05&0.05&0.80\end{pmatrix}\begin{pmatrix}43.0\\29.5\\27.5\end{pmatrix}=\begin{pmatrix}45.100\\29.275\\25.625\end{pmatrix},\quad\ldots.\]Uiteraard zullen de aantallen voertuigen gehele getallen moeten zijn; een alternatief is om niet de aantallen voertuigen in de vectoren op te nemen, maar de percentages van het totale wagenpark. Later zullen we zien dat we het verloop heel gedetailleerd kunnen beschrijven en dat we ook kunnen voorspellen wat er in de toekomst gaat gebeuren met de verdeling van de voertuigen over de drie vestigingen.
Laatst gewijzigd op 22 maart 2021
 Onderwijs
Onderwijs

