Lineaire Algebra – Stelsels lineaire vergelijkingen – De matrix van een lineaire afbeelding

We hebben gezien dat elke matrixafbeelding een lineaire afbeelding is. Het omgekeerde geldt ook: iedere lineaire afbeelding kan worden gezien als een matrixafbeelding.

Stelling: Laat \(T:\mathbb{R}^n\to\mathbb{R}^m\) een lineaire afbeelding zijn. Dan bestaat er een unieke \(m\times n\) matrix \(A\) zodat \(T(\mathbf{x})=A\mathbf{x}\) voor alle \(\mathbf{x}\in\mathbb{R}^n\).
Deze matrix \(A\) wordt gegeven door

\[A=\Bigg(T(\mathbf{e}_1)\;T(\mathbf{e}_2)\;\ldots\;T(\mathbf{e}_n)\Bigg)\quad\text{met}\quad\mathbf{e}_1=\begin{pmatrix}1\\0\\0\\\vdots\\0\\0\end{pmatrix}, \;\mathbf{e}_2=\begin{pmatrix}0\\1\\0\\\vdots\\0\\0\end{pmatrix},\;\ldots,\;\mathbf{e}_n=\begin{pmatrix}0\\0\\0\\\vdots\\0\\1\end{pmatrix}.\]

De matrix \(A\) heet de standaardmatrix van de lineaire afbeelding \(T\).

De vectoren \(\mathbf{e}_1,\mathbf{e}_2,\ldots,\mathbf{e}_n\) zijn de kolommen van de \(n\times n\) eenheidsmatrix \(I_n\).

Bewijs: Merk op dat \[\mathbf{x}=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=I_n\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} =\Bigg(\mathbf{e}_1\;\mathbf{e}_2\;\ldots\;\mathbf{e}_n\Bigg)\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} =x_1\mathbf{e}_1+x_2\mathbf{e}_2+\cdots+x_n\mathbf{e}_n.\]

Dan volgt uit de lineariteit van \(T\) dat

\[T(\mathbf{x})=T(x_1\mathbf{e}_1+x_2\mathbf{e}_2+\cdots+x_n\mathbf{e}_n)=x_1T(\mathbf{e}_1)+x_2T(\mathbf{e}_2)+\cdots+x_nT(\mathbf{e}_n) =\Bigg(T(\mathbf{e}_1)\;T(\mathbf{e}_2)\;\ldots\;T(\mathbf{e}_n)\Bigg)\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=A\mathbf{x}.\]

Voorbeeld: Als \(T:\mathbb{R}^2\to\mathbb{R}^2\) de afbeelding is die elk punt in \(\mathbb{R}^2\) roteert om de oorsprong over een hoek \(\varphi\), tegen de wijzers van de klok in voor positieve waarden van \(\varphi\), dan geldt: \(T\) is een lineaire afbeelding en \(T(\mathbf{x})=A\mathbf{x}\) met

\[A=\begin{pmatrix}\cos(\varphi)&-\sin(\varphi)\\\sin(\varphi)&\cos(\varphi)\end{pmatrix}.\]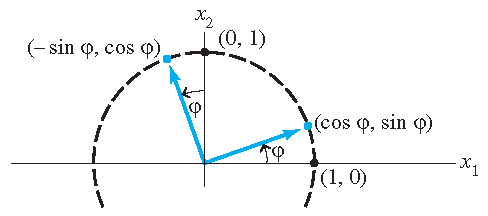

In het plaatje is te zien dat als \(\mathbf{e}_1=\begin{pmatrix}1\\0\end{pmatrix}\) en \(\mathbf{e}_2=\begin{pmatrix}0\\1\end{pmatrix}\), dan geldt: \(T(\mathbf{e}_1)=\begin{pmatrix}\cos(\varphi)\\\sin(\varphi)\end{pmatrix}\) en \(T(\mathbf{e}_2)=\begin{pmatrix}-\sin(\varphi)\\\cos(\varphi)\end{pmatrix}\).

Andere voorbeelden van meetkundige lineaire afbeeldingen in \(\mathbb{R}^2\):

• Spiegelingen:
  • spiegeling in de \(x_1\)-as: \(\begin{pmatrix}1&0\\0&-1\end{pmatrix}\);
  
  
  • spiegeling in de \(x_2\)-as: \(\begin{pmatrix}-1&0\\0&1\end{pmatrix}\);
  
  
  • spiegeling in de lijn \(x_2=x_1\): \(\begin{pmatrix}0&1\\1&0\end{pmatrix}\);
  
  
  • spiegeling in de lijn \(x_2=-x_1\): \(\begin{pmatrix}0&-1\\-1&0\end{pmatrix}\);
  
  
  • spiegeling in de oorsprong: \(\begin{pmatrix}-1&0\\0&-1\end{pmatrix}\). Merk op dat dit hetzelfde is als een rotatie over een hoek \(\pi\).
• Projecties:
  • projectie op de \(x_1\)-as: \(\begin{pmatrix}1&0\\0&0\end{pmatrix}\);
  
  
  • projectie op de \(x_2\)-as: \(\begin{pmatrix}0&0\\0&1\end{pmatrix}\).

Definitie: Een afbeelding \(T:\mathbb{R}^n\to\mathbb{R}^m\) heet surjectief als elke vector in \(\mathbb{R}^m\) het beeld is van minstens één vector in \(\mathbb{R}^n\).

Definitie: Een afbeelding \(T:\mathbb{R}^n\to\mathbb{R}^m\) heet injectief als elke vector in \(\mathbb{R}^m\) het beeld is van hoogstens één vector in \(\mathbb{R}^n\).

Stelling: Laat \(T:\mathbb{R}^n\to\mathbb{R}^m\) een lineaire afbeelding zijn. Dan geldt: \(T\) is injectief dan en slechts dan als de vergelijking \(T(\mathbf{x})=\mathbf{0}\) alleen de triviale oplossing \(\mathbf{x}=\mathbf{0}\) heeft.

Stelling: Laat \(T:\mathbb{R}^n\to\mathbb{R}^m\) een lineaire afbeelding zijn en laat \(A\) de standaardmatrix van \(T\) zijn. Dan geldt:

1. \(T\) is surjectief dan en slechts dan als de kolommen van \(A\) \(\mathbb{R}^m\) opspannen;


2. \(T\) is injectief dan en slechts dan als de kolommen van \(A\) lineair onafhankelijk zijn.

---

Laatst gewijzigd op 22 maart 2021