Linear Algebra – Systems of linear equations – The matrix of a linear transformation

We have seen that every matrix transformation is a linear transformation. The other way around is also true: every linear transformation can be seen as a matrix transformation.

Theorem: Let \(T:\mathbb{R}^n\to\mathbb{R}^m\) be a linear transformation. Then there exists a unique \(m\times n\) matrix \(A\) such that \(T(\mathbf{x})=A\mathbf{x}\) for all \(\mathbf{x}\in\mathbb{R}^n\).
This matrix \(A\) is given by

\[A=\Bigg(T(\mathbf{e}_1)\;T(\mathbf{e}_2)\;\ldots\;T(\mathbf{e}_n)\Bigg)\quad\text{with}\quad\mathbf{e}_1=\begin{pmatrix}1\\0\\0\\\vdots\\0\\0\end{pmatrix}, \;\mathbf{e}_2=\begin{pmatrix}0\\1\\0\\\vdots\\0\\0\end{pmatrix},\;\ldots,\;\mathbf{e}_n=\begin{pmatrix}0\\0\\0\\\vdots\\0\\1\end{pmatrix}.\]

The matrix \(A\) is called the standard matrix of the linear transformation \(T\).

The vectors \(\mathbf{e}_1,\mathbf{e}_2,\ldots,\mathbf{e}_n\) are the columns of the \(n\times n\) identity matrix \(I_n\).

Proof: Note that \[\mathbf{x}=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=I_n\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} =\Bigg(\mathbf{e}_1\;\mathbf{e}_2\;\ldots\;\mathbf{e}_n\Bigg)\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} =x_1\mathbf{e}_1+x_2\mathbf{e}_2+\cdots+x_n\mathbf{e}_n.\]

Then the linearity of \(T\) implies that

\[T(\mathbf{x})=T(x_1\mathbf{e}_1+x_2\mathbf{e}_2+\cdots+x_n\mathbf{e}_n)=x_1T(\mathbf{e}_1)+x_2T(\mathbf{e}_2)+\cdots+x_nT(\mathbf{e}_n) =\Bigg(T(\mathbf{e}_1)\;T(\mathbf{e}_2)\;\ldots\;T(\mathbf{e}_n)\Bigg)\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=A\mathbf{x}.\]

Example: If \(T:\mathbb{R}^2\to\mathbb{R}^2\) is the transformation that rotates each point in \(\mathbb{R}^2\) about the origin through an angle \(\varphi\), with counterclockwise rotation for positive values of \(\varphi\), then we have: \(T\) is a linear transformation and \(T(\mathbf{x})=A\mathbf{x}\) with

\[A=\begin{pmatrix}\cos(\varphi)&-\sin(\varphi)\\\sin(\varphi)&\cos(\varphi)\end{pmatrix}.\]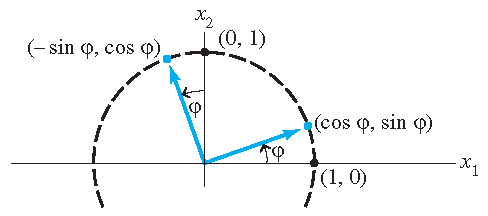

In the picture it is shown that if \(\mathbf{e}_1=\begin{pmatrix}1\\0\end{pmatrix}\) and \(\mathbf{e}_2=\begin{pmatrix}0\\1\end{pmatrix}\), then: \(T(\mathbf{e}_1)=\begin{pmatrix}\cos(\varphi)\\\sin(\varphi)\end{pmatrix}\) and \(T(\mathbf{e}_2)=\begin{pmatrix}-\sin(\varphi)\\\cos(\varphi)\end{pmatrix}\).

Other examples of geometric linear transformations in \(\mathbb{R}^2\):

• Reflections:
  • reflection in the \(x_1\)-axis: \(\begin{pmatrix}1&0\\0&-1\end{pmatrix}\);
  
  
  • reflection in the \(x_2\)-axis: \(\begin{pmatrix}-1&0\\0&1\end{pmatrix}\);
  
  
  • reflection in the line \(x_2=x_1\): \(\begin{pmatrix}0&1\\1&0\end{pmatrix}\);
  
  
  • reflection in the line \(x_2=-x_1\): \(\begin{pmatrix}0&-1\\-1&0\end{pmatrix}\);
  
  
  • reflection in the origin: \(\begin{pmatrix}-1&0\\0&-1\end{pmatrix}\). Merk op dat dit hetzelfde is als een rotatie over een hoek \(\pi\).
• Projections:
  • projection onto the \(x_1\)-axis: \(\begin{pmatrix}1&0\\0&0\end{pmatrix}\);
  
  
  • projection onto the \(x_2\)-axis: \(\begin{pmatrix}0&0\\0&1\end{pmatrix}\).

Definition: A transformation \(T:\mathbb{R}^n\to\mathbb{R}^m\) is called onto if each vector in \(\mathbb{R}^m\) is the image of at least one vector in \(\mathbb{R}^n\).

Definition: A transformation \(T:\mathbb{R}^n\to\mathbb{R}^m\) is called one-to-one if each vector in \(\mathbb{R}^m\) is the image of at most one vector in \(\mathbb{R}^n\).

Theorem: Let \(T:\mathbb{R}^n\to\mathbb{R}^m\) be a linear transformation. Then we have: \(T\) is one-to-one if and only if the equation \(T(\mathbf{x})=\mathbf{0}\) has only the trivial solution \(\mathbf{x}=\mathbf{0}\).

Theorem: Let \(T:\mathbb{R}^n\to\mathbb{R}^m\) be a linear transformation and let \(A\) be the standard matrix of \(T\). Then we have:

1. \(T\) is onto if and only if the columns of \(A\) span \(\mathbb{R}^m\);


2. \(T\) is one-to-one if and only if the columns of \(A\) are linear independent.

---

Last modified on March 22, 2021