Lineaire Algebra – Stelsels lineaire vergelijkingen – Toepassingen 1

Het gesloten Leontief input-output model in de economie

Een eenvoudig model van een kleine economie werkt alsvolgt: neem aan dat de economie kan worden opgedeeld in drie sectoren \(A\), \(B\) en \(C\) en beschouw de input en de output van deze sectoren. We gaan er daarbij vanuit dat alle output binnen de economie blijft (gesloten model). We hebben dan bijvoorbeeld het volgende overzicht:

\[\begin{array}{|ccc|c|} \hline A&B&C&\\ \hline 0.0&0.6&0.3&A\\ 0.4&0.1&0.5&B\\ 0.6&0.3&0.2&C\\ \hline \end{array}\]

In iedere kolom wordt aangegeven hoe de output van die desbetreffende sector wordt verdeeld over de drie sectoren. In iedere rij wordt aangegeven hoeveel van de output van de drie sectoren wordt afgenomen door die betreffende sector.

De Russische econoom Wassily Leontief (1906-1999) toonde aan dat er een evenwicht bestaat in de volgende zin: als we de productie van de drie sectoren \(P_A\), \(P_B\) en \(P_C\) noemen, dan willen we dat

\[P_A=0.6P_B+0.3P_C,\quad P_B=0.4P_A+0.1P_B+0.5P_C\quad\text{en}\quad P_C=0.6P_A+0.3P_B+0.2P_C.\]

Dat wil zeggen: we zoeken een oplossing van het homogene stelsel

\[\left\{\begin{array}{r}P_A-0.6P_B-0.3P_C=0\\-0.4P_A+0.9P_B-0.5P_C=0\\-0.6P_A-0.3P_B+0.8P_C=0\end{array}\right.\quad\Longrightarrow\quad \begin{pmatrix}1&-0.6&-0.3\\-0.4&0.9&-0.5\\-0.6&-0.3&0.8\end{pmatrix}\sim\begin{pmatrix}1&-0.6&-0.3\\0&0.66&-0.62\\0&-0.66&0.62\end{pmatrix} \sim\begin{pmatrix}1&-0.60&-0.30\\0&0.66&-0.62\\0&0&0\end{pmatrix}.\]

De algemene oplossing kan geschreven worden als \(\begin{pmatrix}P_A\\P_B\\P_C\end{pmatrix}=k\begin{pmatrix}0.285\\0.310\\0.330\end{pmatrix}\) met \(k\) een willekeurige (positieve) constante. We kunnen deze constante zo kiezen dat de som van de elementen van deze vector gelijk is aan de totale productie van de drie sectoren.

Een ander voorbeeld is:

\[\begin{array}{|ccc|c|} \hline A&B&C&\\ \hline \frac{1}{2}&\frac{1}{3}&\frac{1}{4}&A\\ \frac{1}{4}&\frac{1}{3}&\frac{1}{4}&B\\ \frac{1}{4}&\frac{1}{3}&\frac{1}{2}&C\\ \hline \end{array}\]

In dat geval vinden we: \(P_A=\frac{1}{2}P_A+\frac{1}{3}P_B+\frac{1}{4}P_C\), \(P_B=\frac{1}{4}P_A+\frac{1}{3}P_B+\frac{1}{4}P_C\) en \(P_C=\frac{1}{4}P_A+\frac{1}{3}P_B+\frac{1}{2}P_C\) oftewetl:

\[\left\{\begin{array}{r}\frac{1}{2}P_A-\frac{1}{3}P_B-\frac{1}{4}P_C=0\\-\frac{1}{4}P_A+\frac{2}{3}P_B-\frac{1}{4}P_C=0\\ -\frac{1}{4}P_A-\frac{1}{3}P_B+\frac{1}{2}PC=0\end{array}\right.\quad\Longrightarrow\quad \begin{pmatrix}\frac{1}{2}&-\frac{1}{3}&-\frac{1}{4}\\-\frac{1}{4}&\frac{2}{3}&-\frac{1}{4}\\-\frac{1}{4}&-\frac{1}{3}&\frac{1}{2}\end{pmatrix} \sim\begin{pmatrix}\frac{1}{2}&-\frac{1}{3}&-\frac{1}{4}\\0&\frac{1}{2}&-\frac{3}{8}\\0&-\frac{1}{2}&\frac{3}{8}\end{pmatrix} \sim\begin{pmatrix}\frac{1}{2}&0&-\frac{1}{2}\\0&\frac{1}{2}&-\frac{3}{8}\\0&0&0\end{pmatrix}.\]

De algemene oplossing is \(\begin{pmatrix}P_A\\P_B\\P_C\end{pmatrix}=k\begin{pmatrix}4\\3\\4\end{pmatrix}\) met \(k\) een willekeurige (positieve) constante. Met bijvoorbeeld \(k=\frac{1}{11}\) wordt de totale productie \(1\).

Balans in chemische reactievergelijkingen

Een chemische reactievergelijking beschrijft de hoeveelheden moleculen die bij een chemische reactie betrokken zijn. Bijvoorbeeld: bij de verbranding van propaangas reageert propaan met zuurstof, waardoor er kooldioxide en water ontstaat:

\[x_1\,C_3H_8+x_2\,O_2\;\;\longrightarrow\;\;x_3\,CO_2+x_4\,H_2O.\]

Om deze vergelijking in "balans" te brengen, dient een chemicus gehele getallen \(x_1\),\(x_2\), \(x_3\) en \(x_4\) te vinden zodat de totale aantallen atomen koolstof (C), waterstof (H) en zuurstof (O) links en rechts aan elkaar gelijk zijn. Dit kan worden gedaan door er een vectorvergelijking van te maken, waarbij de kentallen van de vectoren de aantallen atomen koolstof (C), waterstof (H) en zuurstof (O) respectievelijk aangeven: \(\begin{pmatrix}C\\H\\O\end{pmatrix}\). Dan volgt:

\[x_1\begin{pmatrix}3\\8\\0\end{pmatrix}+x_2\begin{pmatrix}0\\0\\2\end{pmatrix}=x_3\begin{pmatrix}1\\0\\2\end{pmatrix} +x_4\begin{pmatrix}0\\2\\1\end{pmatrix}.\]

Dit levert een homogene vectorvergelijking:

\[x_1\begin{pmatrix}3\\8\\0\end{pmatrix}+x_2\begin{pmatrix}0\\0\\2\end{pmatrix}-x_3\begin{pmatrix}1\\0\\2\end{pmatrix} -x_4\begin{pmatrix}0\\2\\1\end{pmatrix}=\mathbf{0}:\quad\begin{pmatrix}3&0&-1&0\\8&0&0&-2\\0&2&-2&-1\end{pmatrix} \sim\begin{pmatrix}4&0&0&-1\\0&4&0&-5\\0&0&4&-3\end{pmatrix}\quad\Longrightarrow\quad\left\{\begin{array}{l}x_1=\frac{1}{4}x_4\\ x_2=\frac{5}{4}x_4\\x_3=\frac{3}{4}x_4\\x_4\;\text{is vrij.}\end{array}\right.\]

Omdat we (positieve) gehele getallen als oplossingen moeten hebben, kiezen we nu \(x_4=4\) (voor de kleinste gehele getallen):

\[C_3H_8+5\,O_2\;\;\longrightarrow\;\;3\,CO_2+4\,H_20.\]

Een ander voorbeeld is:

\[x_1\,NH_3+x_2\,O_2\;\;\longrightarrow\;\;x_3\,NO+x_4\,H_2O.\]

Dan volgt met vectoren \(\begin{pmatrix}N\\H\\O\end{pmatrix}\):

\[x_1\begin{pmatrix}1\\3\\0\end{pmatrix}+x_2\begin{pmatrix}0\\0\\2\end{pmatrix}=x_3\begin{pmatrix}1\\0\\1\end{pmatrix}+x_4\begin{pmatrix}0\\2\\1\end{pmatrix}:\; \begin{pmatrix}1&0&-1&0\\3&0&0&-2\\0&2&-1&-1\end{pmatrix}\sim\begin{pmatrix}1&0&-1&0\\0&0&3&-2\\0&2&-1&-1\end{pmatrix} \sim\begin{pmatrix}1&0&0&-\frac{2}{3}\\0&2&0&-\frac{5}{3}\\0&0&1&-\frac{2}{3}\end{pmatrix}\;\Longrightarrow\; \left\{\begin{array}{l}x_1=\frac{2}{3}x_4\\x_2=\frac{5}{6}x_4\\x_3=\frac{2}{3}x_4\\x_4\;\text{is vrij.}\end{array}\right.\]

We vinden nu de kleinste oplossing met (positieve) gehele getallen als we \(x_4=6\) nemen. Dus:

\[4\,NH_3+5O_2\;\;\longrightarrow\;\;4\,NO+6\,H_2O.\]

Netwerkstromen

Beschouw bijvoorbeeld de verkeersstromen in een wegennetwerk, waarbij op sommige plaatsen het aantal passerende voertuigen wordt geteld. Rekening houdend met eenrichtingsverkeer, worden de aantallen per uur weergegeven in het plaatje.

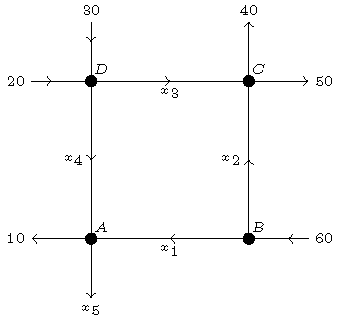
Met behulp van deze gegevens kunnen we het volledige patroon van de verkeersstromen achterhalen. Bij elk van de kruispunten stellen we daarvoor een evenwichtsvergelijking op; het aantal binnenkomende voertuigen is gelijk aan het aantal uitgaande voertuigen. Dan volgt:

\[\left\{\begin{array}{l}A:\;x_1+x_4=x_5+10\\[2.5mm]B:\;60=x_1+x_2\\[2.5mm]C:\;x_2+x_3=40+50\\[2.5mm]D:\;20+30=x_3+x_4\end{array}\right.\quad\Longrightarrow\quad \left\{\begin{array}{rrrrrcl}x_1&&&+x_4&-x_5&=&10\\[2.5mm]x_1&+x_2&&&&=&60\\[2.5mm]&x_2&+x_3&&&=&90\\[2.5mm]&&x_3&+x_4&&=&50.\end{array}\right.\]

Dit is een inhomogeen stelsel lineaire vergelijkingen, dus:

\[\left(\left.\begin{matrix}1&0&0&1&-1\\1&1&0&0&0\\0&1&1&0&0\\0&0&1&1&0\end{matrix}\,\right|\,\begin{matrix}10\\60\\90\\50\end{matrix}\right) \sim\;\;\cdots\;\;\sim\left(\left.\begin{matrix}1&0&0&1&0\\0&1&0&-1&0\\0&0&1&1&0\\0&0&0&0&1\end{matrix}\,\right|\,\begin{matrix}20\\40\\50\\10\end{matrix}\right) \quad\Longrightarrow\quad\left\{\begin{array}{l}x_1=20-x_4\\x_2=40+x_4\\x_3=50-x_4\\x_4\;\text{is vrij}\\x_5=10.\end{array}\right.\]

Omdat we hier te maken hebben met eenrichtingsverkeer, mogen de variabelen niet negatief worden (dan zou het verkeer in de andere richting rijden). We concluderen dus dat \(0\leq x_4\leq 20\). Merk op dat hieruit volgt dat ook \(0\leq x_1\leq 20\), \(40\leq x_2\leq 60\) en \(30\leq x_3\leq 50\).

Nog een voorbeeld, weer met eenrichtingsverkeer:

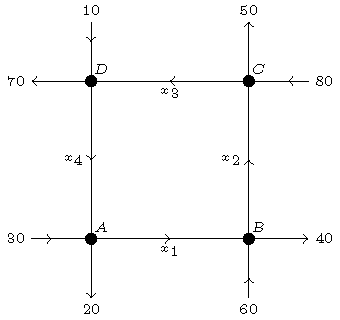
Nu vinden we:

\[\left\{\begin{array}{l}A:\;30+x_4=20+x_1\\[2.5mm]B:\;60+x_1=40+x_2\\[2.5mm]C:\;80+x_2=50+x_3\\[2.5mm]D:\;10+x_3=70+x_4\end{array}\right.\quad\Longrightarrow\quad \left\{\begin{array}{rrrrcr}x_1&&&-x_4&=&10\\[2.5mm]-x_1&+x_2&&&=&20\\[2.5mm]&-x_2&+x_3&&=&30\\[2.5mm]&&-x_3&+x_4&=&-60\end{array}\right.\]

en dus

\[\left(\left.\begin{matrix}1&0&0&-1\\-1&1&0&0\\0&-1&1&0\\0&0&-1&1\end{matrix}\,\right|\,\begin{matrix}10\\20\\30\\-60\end{matrix}\right) \sim\;\;\cdots\;\;\sim\left(\left.\begin{matrix}1&0&0&-1\\0&1&0&-1\\0&0&1&-1\\0&0&0&0\end{matrix}\,\right|\,\begin{matrix}10\\30\\60\\0\end{matrix}\right) \quad\Longrightarrow\quad\left\{\begin{array}{l}x_1=10+x_4\\x_2=30+x_4\\x_3=60+x_4\\x_4\;\text{is vrij.}\end{array}\right.\]

---

Laatst gewijzigd op 22 maart 2021