Analyse – Functies van meerdere variabelen – Functies van twee variabelen

Definitie: Het maximale of natuurlijke domein \(D\) van een functie \(f\) van twee variabelen is de verzameling van alle punten \((x,y)\) waarvoor \(f(x,y)\) bestaat.

Opmerking: het werkelijke domein van de functie zou een deelverzameling van het maximale of natuurlijke domein kunnen zijn.

Definitie: Het bereik \(B\) van een functie \(f\) van twee variabelen is de verzameling van alle mogelijke waarden van \(f(x,y)\), dat wil zeggen: \(B=\{f(x,y)\,|\,(x,y)\in D\}\).

Definitie: De grafiek van een functie \(f\) van twee variabelen met domein \(D\) is de verzameling in \(\mathbb{R}^3\) van alle punten \((x,y,f(x,y))\) met \((x,y)\in D\).

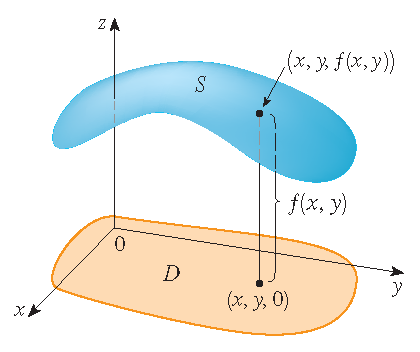
In het algemeen is het vrij lastig om de grafiek van een functie van twee variabelen met de hand te tekenen:

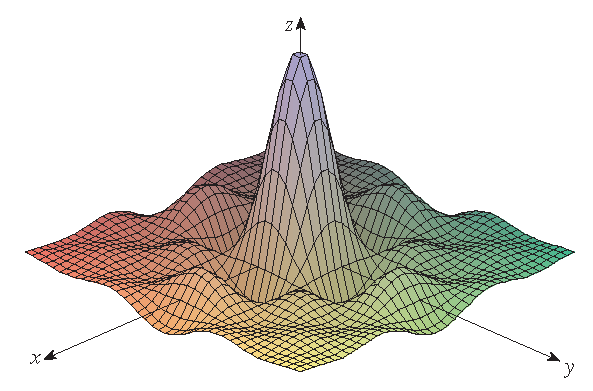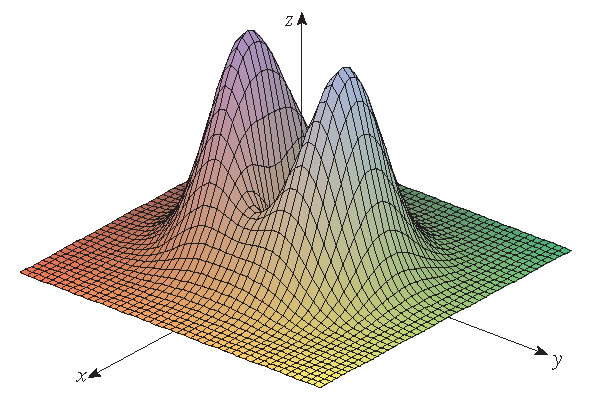
the graph of \(f(x,y)=(x^2+3y^2)e^{-x^2-y^2}\)	the graph of \(g(x,y)=\displaystyle\frac{\sin(x)\sin(y)}{xy}\)

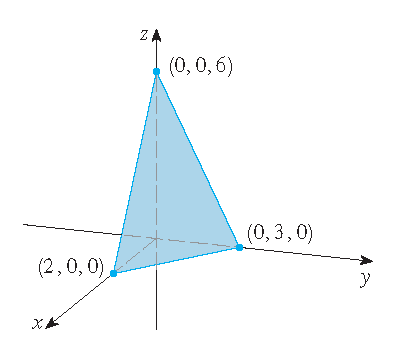
Echter, in sommige eenvoudige gevallen is het wel mogelijk om de grafiek handmatig te tekenen:

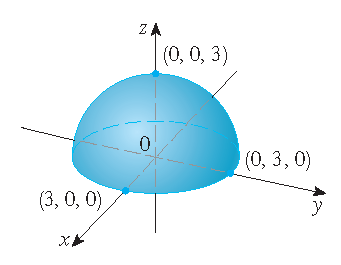the graph of \(f(x,y)=6-3x-2y\)	the graph of \(g(x,y)=\sqrt{9-x^2-y^2}\)

Definitie: Een niveaukromme van een functie \(f\) van twee variabelen is een krommen in \(\mathbb{R}^2\) met vergelijking \(f(x,y)=k\) met \(k\) een constante (in het bereik van \(f\)). Een plot met diverse niveaukrommen heet een hoogtekaart.

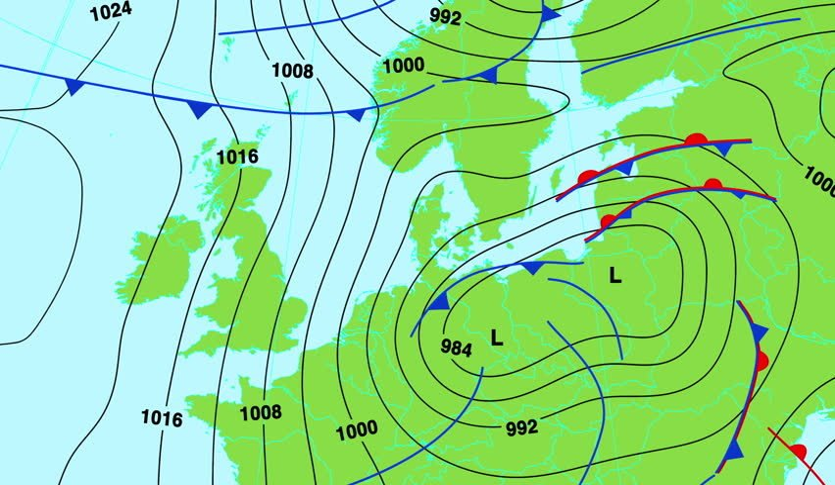
Een hoogtekaart van atmosferische luchtdruk boven Centraal Europa

Voorbeelden van niveaukrommen:

1. hoogtelijnen met de hoogte boven zeeniveau in topografische kaarten van bergachtige gebieden;


2. lijnen met constante atmosferische luchtdruk (isobaren) in weerkaarten;


3. lijnen met constante temperatuur (isothermen) in weerkaarten.

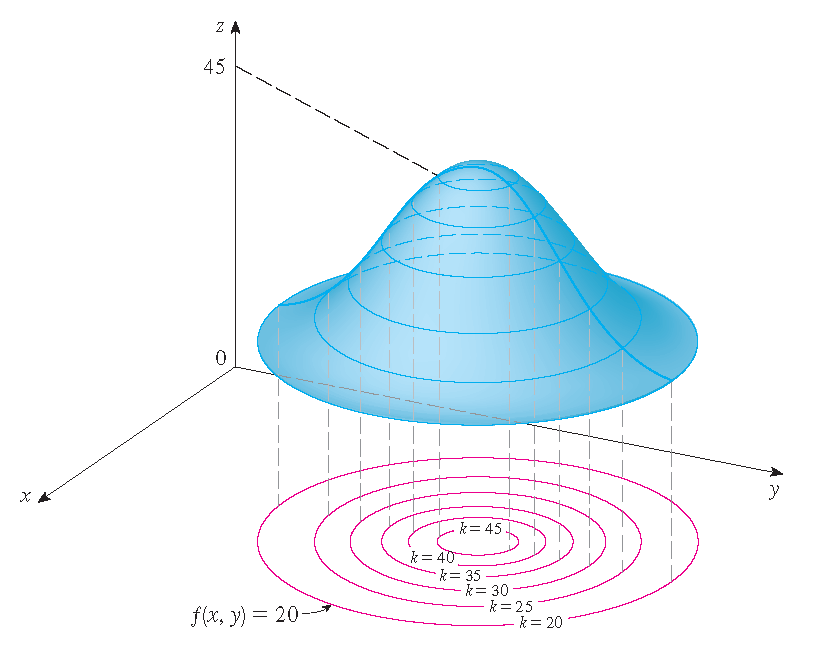
Niveaukrommen en de grafiek van een functie:

Toepassing:

Stewart §14.1: Opgave 39
De Body Mass Index (BMI) of Quetelet Index (QI) van een persoon wordt gedefinieerd door

\[B(m,h)=\frac{m}{h^2},\]

waarbij \(m\) de massa (in kilogrammen) is van de persoon en \(h\) de lengte (in meters).

De niveaukrommen \(B(m,h)=18\), \(B(m,h)=25\), \(B(m,h)=30\) en \(B(m,h)=40\) zijn getekend in het plaatje:

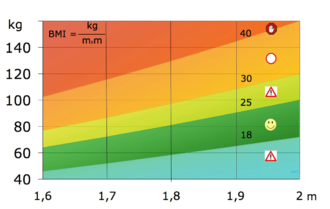
Een ruwe richtlijn voor de BMI is:

\[\begin{array}{|ccc|ccc|} \hline < 18 &:& \text{ondergewicht} & 25 - 30 &:& \text{overgewicht}\\ 18 - 25 &:& \text{normaal} & > 30 &:& \text{obese}\\ \hline \end{array}\]

Dus: het gebied behorend bij een optimaal BMI is groen in het plaatje.

De BMI van een persoon, die \(62\) kg weegt en \(152\) cm lang is, is

\[B(62,1.52)=\frac{62}{(1.52)^2}\approx26.835.\]

Hieruit volgt dat de persoon lichtelijk te zwaar is.

Stewart §14.1: Opgave 40
Voor een persoon, die \(200\) cm lang is en \(80\) kg weegt, is de BMI gelijk aan

\[B(80,2)=\frac{80}{2^2}=20.\]

Voor een persoon van \(180\) cm lang met dezelfde BMI volgt:

\[B(m,1.8)=\frac{m}{(1.8)^2}=20\quad\Longrightarrow\quad m=20(1.8)^2=64.8.\]

Voor een persoon van \(170\) cm lang met dezelfde BMI volgt:

\[B(m,1.7)=\frac{m}{(1.7)^2}=20\quad\Longrightarrow\quad m=20(1.7)^2=57.8.\]

Conclusie: een persoon van \(180\) cm lang, die \(64.8\) kg weegt, en een persoon van \(170\) cm lang, die \(57.8\) kg weegt, hebben (exact) dezelfde BMI:

\[B(80,2)=B(64.8,1.8)=B(57.8,1.7)=20.\]

Voor een persoon, die \(70\) kg weegt, met dezelfde BMI volgt:

\[B(70,h)=\frac{70}{h^2}=20\quad\Longrightarrow\quad h^2=\frac{7}{2}\quad\Longrightarrow\quad h=\frac{1}{2}\sqrt{14}\approx1.87.\]

Conclusie: een persoon van \(187\) cm lang, die \(70\) kg weegt, heeft (ongeveer) dezelfde BMI:

\[B(70,1.87)\approx20.\]

---

Laatst gewijzigd op 15 september 2021