OnderwijsAnalyse – Functies van meerdere variabelen – Raakvlakken en lineaire benaderingen
Van raaklijn naar raakvlak
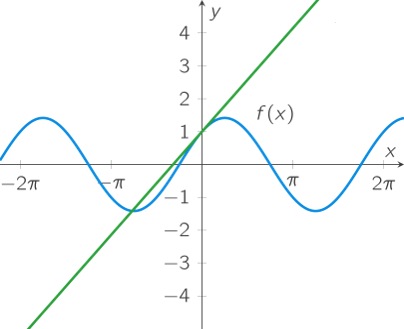
Als \(y=f(x)\), dan kan de raaklijn aan de grafiek van \(f\) door \((a,f(a))\) worden geschreven als: \(y-f(a)=r(x-a)\) met \(r=\displaystyle\frac{dy}{dx}\bigg|_{x=a}=f'(a)\). Dus: \(y=f(a)+f'(a)(x-a)\). De functie \(L(x)=f(a)+f'(a)(x-a)\) heet de linearisering van \(f\) in het punt \(a\).
Definitie: Het raakvlak aan de grafiek van een functie \(f\) van twee variabelen in het punt \(P\) is het vlak door de raaklijnen \(T_1\) en \(T_2\) aan elk tweetal krommen \(\mathcal{C}_1\) en \(\mathcal{C}_2\) door \(P\) op het oppervlak \(z=f(x,y)\).
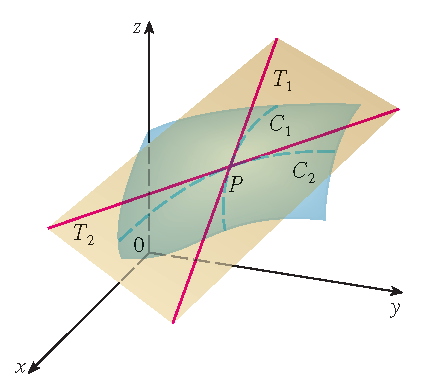
Stelling: Neem aan dat \(f\) continue partiële afgeleiden heeft. Een vergelijking van het raakvlak aan het oppervlak \(z=f(x,y)\), de grafiek van \(f\), in het punt \((a,b,f(a,b))\) is
\[z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b).\]Definitie: De functie
\[L(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\]heet de linearisering van \(f\) in het punt \((a,b)\).
Differentieerbaarheid
Definitie: Een functie \(f\) van twee variabelen heet differentieerbaar in het punt \((a,b)\) als
\[\lim\limits_{(x,y)\to(a,b)}\frac{f(x,y)-L(x,y)}{\sqrt{(x-a)^2+(y-b)^2}}=0.\]Stelling: Als de partiële afgeleiden \(f_x\) en \(f_y\) bestaan in de buurt van \((a,b)\) en continu zijn in \((a,b)\), dan is \(f\) differentieerbaar in \((a,b)\).
Voorbeeld: De functie \(f(x,y)=\displaystyle\left\{\begin{array}{ll}\displaystyle\frac{xy}{x^2+y^2},&(x,y)\neq(0,0)\\[2.5mm] 0,&(x,y)=(0,0)\end{array}\right.\) is niet differentieerbaar in \((0,0)\).
Differentialen
Definitie: Voor een differentieerbare functie \(f\) van twee variabelen, \(z=f(x,y)\), definiëren we de differentialen \(dx\) en \(dy\) als onafhankelijke variabelen. Dan wordt de (totale) differentiaal \(dz\) gedefinieerd door
\[dz=f_x(x,y)\,dx+f_y(x,y)\,dy.\]Toepassingen:
1) We willen de rand schilderen van dit zwembad met afmetingen \(10\times5\) meter.
Om de juiste hoeveelheid verf te kopen, gebruiken we differentialen om de (totale) oppervlakte te schatten van de rand met een breedte van \(20\) cm.
Stel dat \(x=10\) (de lengte) en \(y=5\) (de breedte), dan is oppervlakte van het zwembad \(A(x,y)=xy\). Dus geldt:
\[dA=\frac{\partial A}{\partial x}\,dx+\frac{\partial A}{\partial y}\,dy=y\,dx+x\,dy.\]Hieruit volgt: \(dA=5\cdot(0.4)+10\cdot(0.4)=6\,\text{m}^2\).
Vergelijk met: Stewart, §14.4, Opgave 33.
2) Beschouw een conservenblik met een cirkelvormige bodem en deksel met straal \(r\) en hoogte \(h\).
Het volume is dan gelijk aan: \(V=\pi r^2h\).
Neem nu bijvoorbeeld: \(r=5\) en \(h=10\).
Dan geldt: \(V=\pi\cdot25\cdot10=250\pi\).
Stel nu dat \(dr=0.1\) en \(dh=0.2\) (bijvoorbeeld).
Dan geldt:
\[dV=\frac{\partial V}{\partial r}\,dr+\frac{\partial V}{\partial h}\,dh=2\pi rh\,dr+\pi r^2\,dh=100\pi\cdot0.1+25\pi\cdot0.2=10\pi+5\pi=15\pi.\]
Dit is een benadering van de absolute (maximale) fout \(\Delta V\).
De relatieve (maximale) fout is: \(\displaystyle\frac{\Delta V}{V}\approx\frac{dV}{V}=\frac{15\pi}{250\pi}=\frac{3}{50}\;(6\,\%)\).
Vergelijk met: Stewart, §14.4, Opgaven 34 en 35.
3) Stewart, §14.4, Opgave 41
Eerder hadden we de Body Mass Index (BMI) van een persoon gedefinieerd als
waarbij \(m\) de massa (in kilogrammen) is van de persoon en \(h\) de lengte (in meters).
De partiële afgeleiden zijn
\[B_m(m,h)=\frac{1}{h^2}\quad\text{en}\quad B_h(m,h)=-\frac{2m}{h^3}.\]Dus: de lineaire benadering van \(B(m,h)\) voor een kind met een massa van \(23\) kg en een lengte van \(1.10\) m is
\[L(m,h)=B(23,1.1)+B_m(23,1.1)(m-23)+B_h(23,1.1)(h-1.1)\approx19+0.8264(m-23)-34.5605(h-1.1).\]Als de massa van het kind toeneemt met \(1\) kg en de lengte met \(3\) cm, dan volgt uit deze benadering van de BMI:
\[L(24,1.13)\approx19+0.8264\cdot1−34.5605\cdot0.03\approx18.8.\]Merk op dat de BMI gelijk is aan: \(B(24,1.13)=\displaystyle\frac{24}{(1.13)^2}\approx18.8\).
Laatst gewijzigd op 16 september 2021
