Analyse – Functies van meerdere variabelen – Lokale maxima en minima

Definitie: Een functie \(f\) van twee variabelen heeft een lokaal maximum in \((a,b)\) als \(f(x,y)\leq f(a,b)\) voor \((x,y)\) in de buurt van \((a,b)\). Het getal \(f(a,b)\) heet een lokaal maximum van \(f\).

Evenzo voor een lokaal minimum.

Stelling: Als \(f\) een lokaal maximum of minimum heeft in \((a,b)\) en de eerste-orde partiële afgeleiden van \(f\) bestaan daar, dan is \(f_x(a,b)=0\) en \(f_y(a,b)=0\).

Definitie: Een punt \((a,b)\) heet een kritiek punt of stationair punt van \(f\) als zowel \(f_x(a,b)=0\) als \(f_y(a,b)=0\) of als minstens één van deze partiële afgeleiden niet bestaat.

Gevolg: Als \(f\) een lokaal maximum of minimum heeft in \((a,b)\), dan is \((a,b)\) een kritiek punt van \(f\).

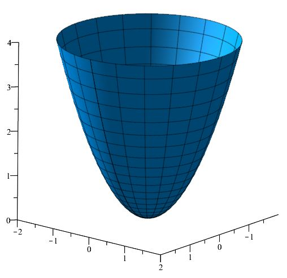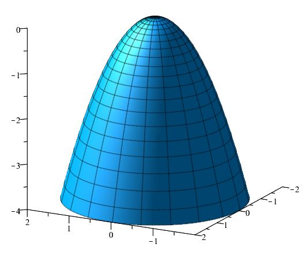
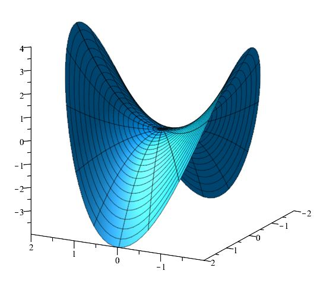
\(f(x,y)=-x^2-y^2\)	\(f(x,y)=x^2-y^2\)	\(f(x,y)=x^2+y^2\)
\(f(0,0)\) is een maximum	\((0,0)\) is een zadelpunt	\(f(0,0)\) is een minimum

Stelling: Neem aan dat de tweede-orde partiële afgeleiden van \(f\) continu zijn op een cirkelschijf met middelpunt \((a,b)\) en neem aan dat \(f_x(a,b)=0\) en \(f_y(a,b)=0\). Laat

\[D(a,b)=\begin{vmatrix}f_{xx}(a,b)&f_{xy}(a,b)\\f_{yx}(a,b)&f_{yy}(a,b)\end{vmatrix}=f_{xx}(a,b)f_{yy}(a,b)-\{f_{xy}(a,b)\}^2.\]

1. Als \(D(a,b)>0\) en \(f_{xx}(a,b)>0\), dan is \(f(a,b)\) een lokaal minimum;


2. Als \(D(a,b)>0\) en \(f_{xx}(a,b)<0\), dan is \(f(a,b)\) een lokaal maximum;


3. Als \(D(a,b)<0\), dan is \(f(a,b)\) noch een lokaal maximum noch een lokaal minimum.

Opmerking: In het derde geval heet het punt \((a,b)\) een zadelpunt van \(f\).

Bewijs: We beschouwen de tweede-orde richtingsafgeleide van \(f\) in de richting van de eenheidsvector \(\mathbf{u}=\langle u_1,u_2\rangle\). De eerste-orde richtingsafgeleide wordt gegeven door

\[D_{\mathbf{u}}f=f_xu_1+f_yu_2.\]

Merk op dat hieruit volgt dat

\[D_{\mathbf{u}}^2f=D_{\mathbf{u}}\left(D_{\mathbf{u}}f\right)=\frac{\partial}{\partial x}\left(D_{\mathbf{u}}f\right)u_1+\frac{\partial}{\partial y}\left(D_{\mathbf{u}}f\right)u_2 =\left(f_{xx}u_1+f_{xy}u_2\right)u_1+\left(f_{yx}u_1+f_{yy}u_2\right)u_2=f_{xx}u_1^2+2f_{xy}u_1u_2+f_{yy}u_2^2.\]

Door kwadraatafsplitsen volgt dat

\[D_{\mathbf{u}}^2f=f_{xx}\left(u_1+\frac{f_{xy}}{f_{xx}}u_2\right)^2+\frac{u_2^2}{f_{xx}}\left(f_{xx}f_{yy}-\{f_{xy}\}^2\right).\]

Stel dat \(D(a,b)>0\) en \(f_{xx}(a,b)>0\). Omdat \(D=f_{xx}f_{yy}-\{f_{xy}\}^2\) en \(f_{xx}\) continue functies zijn, bestaat er een cirkelschijf met middelpunt \((a,b)\) en positieve straal zodat \(D(x,y)>0\) en \(f_{xx}(x,y)>0\) voor \((x,y)\) op die cirkelschijf. Dus: \(D_{\mathbf{u}}^2f>0\) voor \((x,y)\) on die cirkelschijf. Omdat dit geldt voor iedere eenheidsvector \(\mathbf{u}\), concluderen we dat \(f(a,b)\) een lokaal minimum is.

Evenzo, als \(D(a,b)>0\) en \(f_{xx}(a,b)<0\) concluderen we dat \(D_{\mathbf{u}}^2f<0\) voor iedere eenheidsvector \(\mathbf{u}\), waaruit volgt dat \(f(a,b)\) een lokaal maximum is.

Als \(D(a,b)<0\), dan heeft \(D_{\mathbf{u}}^2f\) hetzelfde teken als \(f_{xx}\) als \(u_2=0\) en het tegengestelde teken als \(u_1+\displaystyle\frac{f_{xy}}{f_{xx}}u_2=0\). Hieruit volgt dat \((a,b)\) een zadelpunt van \(f\) is.

Voorbeelden:

1) Toon aan dat \(f(x,y)=2x-x^2+4y-y^2\) slechts één kritiek punt heeft. Heeft \(f\) een lokaal maximum of minimum in dat punt of is het een zadelpunt?

Oplossing: Merk op dat \(f_x(x,y)=2-2x\) en \(f_y(x,y)=4-2y\), waaruit volgt dat \((1,2)\) het enige kritieke of stationaire punt van \(f\) is. Nu geldt \(D(x,y)=\begin{vmatrix}-2&0\\0&-2\end{vmatrix}=4\). Hieruit volgt dat \(D(1,2)=4>0\) en \(f_{xx}(1,2)=-2<0\). Dus: \(f(1,2)=5\) is een lokaal maximum.

Merk op dat \(f(x,y)=5-(x-1)^2-(y-2)^2\).

2) Stewart §14.7, Voorbeeld 3
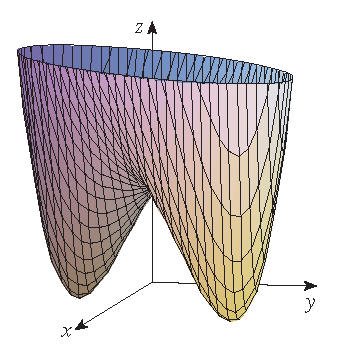
Bepaal de lokale maxima en minima en de zadelpunten van \(f(x,y)=x^4+y^4-4xy+1\).

Oplossing: Merk op dat \(f_x(x,y)=4x^3-4y\) en \(f_y(x,y)=4y^3-4x\). Om de kritieke of staionaire punten te vinden, moeten we oplossen: \(x^3-y=0\) en \(y^3-x=0\). Invullen van \(y=x^3\) in de tweede vergelijking levert:

\[0=x^9-x=x(x^8-1)=x(x^4-1)(x^4+1)=x(x^2-1)(x^2+1)(x^4+1)=x(x-1)(x+1)(x^2+1)(x^4+1).\]

Dus geldt: \(x=0\) of \(x=\pm 1\). Dit leidt tot de kritieke punten \((0,0)\), \((-1,-1)\) en \((1,1)\).

Nu geldt:

\[D(x,y)=\begin{vmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{vmatrix}=\begin{vmatrix}12x^2&-4\\-4&12y^2\end{vmatrix}=144x^2y^2-16.\]

Omdat \(D(0,0)=-16<0\) concluderen we dat \((0,0)\) een zadelpunt is.

Verder geldt: \(D(-1,-1)=128>0\) en \(f_{xx}(-1,-1)=12>0\) waaruit volgt dat \(f(-1,-1)=-1\) een lokaal minimum is.

Ten slotte volgt: \(D(1,1)=128>0\) en \(f_{xx}(1,1)=12>0\) waaruit volgt dat \(f(1,1)=-1\) ook een lokaal minimum is.

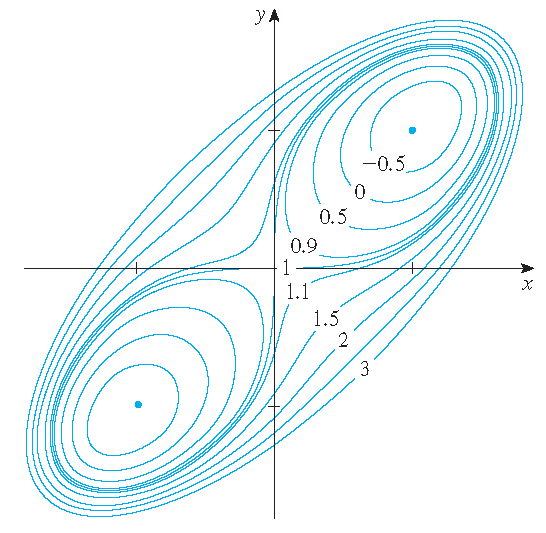Grafiek van \(f(x,y)=x^4+y^4-4xy+1\)	Hoogtekaart van \(f(x,y)=x^4+y^4-4xy+1\)

3) Vergelijk met Stewart §14.7, Voorbeeld 5
Bepaal de kortste afstand van het punt \((1,0,-3)\) tot het vlak \(x+2y+z=4\).

Oplossing: De afstand van een willekeurig punt \((x,y,z)\) tot het punt \((1,0,-3)\) is \(\sqrt{(x-1)^2+y^2+(z+3)^2}\). Als \((x,y,z)\) in het vlak \(x+2y+z=4\) ligt, dan geldt: \(z=4-x-2y\). We zoeken dus een minimum van \(\sqrt{(x-1)^2+y^2+(7-x-2y)^2}\). We kunnen dus ook zoeken naar een minimum van \(f(x,y)=(x-1)^2+y^2+(7-x-2y)^2\). Zoekend naar kritieke punten vinden we

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad2(x-1)-2(7-x-2y)=0\quad\Longleftrightarrow\quad4x+4y-16=0\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad2y-4(7-x-2y)=0\quad\Longleftrightarrow\quad4x+10y-28=0.\end{array}\right.\]

Door de vergelijkingen van elkaar af te trekken vinden we \(6y-12=0\) en dus \(y=2\) waaruit volgt dat \(x=2\). Dus: \((2,2)\) is het enige kritieke punt van \(f\). Omdat \(f_{xx}=4\), \(f_{yy}=10\) en \(f_{xy}=4\), geldt: \(D(x,y)=f_{xx}f_{yy}-\{f_{xy}\}^2=40-16=24>0\) en \(f_{xx}>0\), waaruit volgt dat \(f(2,2)=1+4+1=6\) een lokaal minimum van \(f\) is. We concluderen dat de kortste afstand van het punt \((1,0,-3)\) tot het vlak \(x+2y+z=4\) gelijk aan \(\sqrt{6}\) is.

Toepassingen:

1) Stewart §14.7, Voorbeeld 6
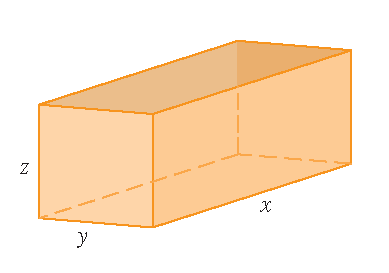
Een rechthoekige doos zonder een deskel wordt gemaakt van \(12\,\text{m}^2\) karton. Bepaal het maximale volume van zo'n doos.

Oplossing: Merk op dat het volume van de doos gelijk is aan \(V=xyz\).

De totale oppervlakte van de vier zijden en de bodem moet gelijk zijn aan \(12\,\text{m}^2\).

Dus moet gelden: \(2xz+2yz+xy=12\).

Dus: \(2(x+y)z=12-xy\) waaruit volgt dat \(z=\displaystyle\frac{12-xy}{2(x+y)}\).

Hieruit volgt dat het volume \(V\) een functie van twee variabelen is: \(V(x,y)=\displaystyle\frac{xy(12-xy)}{2(x+y)}\).

De partiële afgeleiden zijn: \(V_x(x,y)=\displaystyle\frac{y^2(12-2xy-x^2)}{2(x+y)^2}\) en \(V_y(x,y)=\displaystyle\frac{x^2(12-2xy-y^2)}{2(x+y)^2}\).

Voor het maximale volume moeten beide gelijk aan nul zijn.

Omdat \(x\) en \(y\) positief moeten zijn, concluderen we dat \(12-2xy-x^2=0\) en \(12-2xy-y^2=0\).

Hieruit volgt dat \(y=x\) en \(12-2x^2-x^2=0\), dus: \(x=y=2\) en \(z=\displaystyle\frac{12-xy}{2(x+y)}=1\).

We concluderen dat het maximale volume gelijk is aan \(V=2\cdot2\cdot1=4\,\text{m}^2\).

2) Een rechthoekige doos met een deskel wordt gemaakt van \(24\,\text{m}^2\) karton. Bepaal het maximale volume van zo'n doos.

Oplossing: Merk op dat het volume van de doos gelijk is aan \(V=xyz\) met \(2xz+2yz+2xy=24\).

Dit leidt tot \(z=\displaystyle\frac{24-2xy}{2(x+y)}=\frac{12-xy}{x+y}\) en \(V(x,y)=\displaystyle\frac{xy(12-xy)}{x+y}\) met partiële afgeleiden

\(V_x(x,y)=\displaystyle\frac{y^2(12-2xy-x^2)}{(x+y)^2}\) en \(V_y(x,y)=\displaystyle\frac{x^2(12-2xy-y^2)}{(x+y)^2}\).

Voor het maximale volume moeten beide gelijk aan nul zijn.

Omdat \(x\) en \(y\) positief moeten zijn, concluderen we dat \(12-2xy-x^2=0\) en \(12-2xy-y^2=0\).

Hieruit volgt dat \(y=x\) en \(12-2x^2-x^2=0\), dus: \(x=y=2\) en \(z=\displaystyle\frac{12-xy}{x+y}=2\).

We concluderen dat het maximale volume gelijk is aan \(V=2\cdot2\cdot2=8\,\text{m}^2\).

---

Laatst gewijzigd op 23 september 2021