Calculus – Functions of several variables – Local maximum and minimum values

Definition: A function \(f\) of two variables has a local maximum at \((a,b)\) if \(f(x,y)\leq f(a,b)\) when \((x,y)\) is near \((a,b)\). The number \(f(a,b)\) is called a local maximum value of \(f\).

Similarly for a local minimum.

Theorem: If \(f\) has a local maximum or minimum value at \((a,b)\) and the first-order partial derivatives of \(f\) exist there, then \(f_x(a,b)=0\) and \(f_y(a,b)=0\).

Definition: A point \((a,b)\) is called a critical point or stationary point of \(f\) if both \(f_x(a,b)=0\) and \(f_y(a,b)=0\) or if at least one of these partial derivatives does not exist.

Corollary: If \(f\) has a local maximum or minimum at \((a,b)\), then \((a,b)\) is a critical point of \(f\).

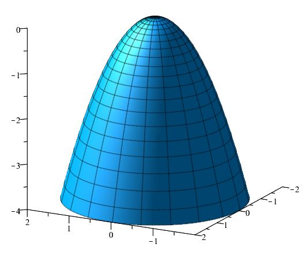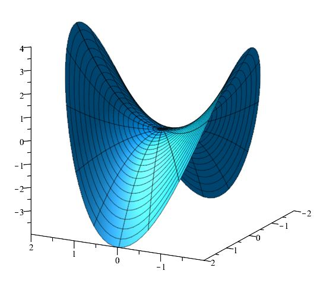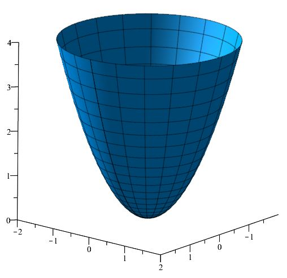\(f(x,y)=-x^2-y^2\)	\(f(x,y)=x^2-y^2\)	\(f(x,y)=x^2+y^2\)
\(f(0,0)\) is a maximum	\((0,0)\) is a saddle point	\(f(0,0)\) is a minimum

Theorem: Suppose that the second-order partial derivatives of \(f\) are continuous on a disk with center \((a,b)\) and suppose that \(f_x(a,b)=0\) and \(f_y(a,b)=0\). Let

\[D(a,b)=\begin{vmatrix}f_{xx}(a,b)&f_{xy}(a,b)\\f_{yx}(a,b)&f_{yy}(a,b)\end{vmatrix}=f_{xx}(a,b)f_{yy}(a,b)-\{f_{xy}(a,b)\}^2.\]

1. If \(D(a,b)>0\) and \(f_{xx}(a,b)>0\), then \(f(a,b)\) is a local minimum value;


2. If \(D(a,b)>0\) and \(f_{xx}(a,b)<0\), then \(f(a,b)\) is a local maximum value;


3. If \(D(a,b)<0\), then \(f(a,b)\) is not a local maximum or minimum value.

Note: In the third case the point \((a,b)\) is called a saddle point of \(f\).

Proof: We consider the second-order directional derivative of \(f\) in the direction of the unit vector \(\mathbf{u}=\langle u_1,u_2\rangle\). The first-order directional derivative is given by

\[D_{\mathbf{u}}f=f_xu_1+f_yu_2.\]

Note that this implies that

\[D_{\mathbf{u}}^2f=D_{\mathbf{u}}\left(D_{\mathbf{u}}f\right)=\frac{\partial}{\partial x}\left(D_{\mathbf{u}}f\right)u_1+\frac{\partial}{\partial y}\left(D_{\mathbf{u}}f\right)u_2 =\left(f_{xx}u_1+f_{xy}u_2\right)u_1+\left(f_{yx}u_1+f_{yy}u_2\right)u_2=f_{xx}u_1^2+2f_{xy}u_1u_2+f_{yy}u_2^2.\]

Completing the square, we obtain that

\[D_{\mathbf{u}}^2f=f_{xx}\left(u_1+\frac{f_{xy}}{f_{xx}}u_2\right)^2+\frac{u_2^2}{f_{xx}}\left(f_{xx}f_{yy}-\{f_{xy}\}^2\right).\]

Let \(D(a,b)>0\) and \(f_{xx}(a,b)>0\). Since \(D=f_{xx}f_{yy}-\{f_{xy}\}^2\) and \(f_{xx}\) are continuous functions, there exists a disk with center \((a,b)\) and positive radius such that \(D(x,y)>0\) and \(f_{xx}(x,y)>0\) whenever \((x,y)\) is on this disk. Therefore, \(D_{\mathbf{u}}^2f>0\) for \((x,y)\) on this disk. Since this holds for every unit vector \(\mathbf{u}\), we conclude that \(f(a,b)\) is a local minimum.

Similarly, if \(D(a,b)>0\) and \(f_{xx}(a,b)<0\) we conclude that \(D_{\mathbf{u}}^2f<0\) for every unit vector \(\mathbf{u}\), which implies that \(f(a,b)\) is a local maximum value.

If \(D(a,b)<0\), then \(D_{\mathbf{u}}^2f\) has the same sign as \(f_{xx}\) if \(u_2=0\) and has the opposite sign if \(u_1+\displaystyle\frac{f_{xy}}{f_{xx}}u_2=0\). This implies that \((a,b)\) is a saddle point of \(f\).

Examples:

1) Show that \(f(x,y)=2x-x^2+4y-y^2\) has only one critical point. Does \(f\) have a local maximum or minimum value at this point or is it a saddle point?

Solution: Note that \(f_x(x,y)=2-2x\) and \(f_y(x,y)=4-2y\), which implies that \((1,2)\) is the only critical or stationary point of \(f\). Now we have \(D(x,y)=\begin{vmatrix}-2&0\\0&-2\end{vmatrix}=4\). This implies that \(D(1,2)=4>0\) and \(f_{xx}(1,2)=-2<0\). Hence: \(f(1,2)=5\) is a local maximum value.

Note that \(f(x,y)=5-(x-1)^2-(y-2)^2\).

2) Stewart §14.7, Example 3
Find the local maximum and minimum values and saddle points of \(f(x,y)=x^4+y^4-4xy+1\).

Solution: Note that \(f_x(x,y)=4x^3-4y\) and \(f_y(x,y)=4y^3-4x\). In order to find the critical or stationary points we have to solve: \(x^3-y=0\) and \(y^3-x=0\). Substituting \(y=x^3\) into the second equation, we obtain:

\[0=x^9-x=x(x^8-1)=x(x^4-1)(x^4+1)=x(x^2-1)(x^2+1)(x^4+1)=x(x-1)(x+1)(x^2+1)(x^4+1).\]

Hence we have: \(x=0\) or \(x=\pm 1\). This leads to the critical points \((0,0)\), \((-1,-1)\) and \((1,1)\).

Now we have:

\[D(x,y)=\begin{vmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{vmatrix}=\begin{vmatrix}12x^2&-4\\-4&12y^2\end{vmatrix}=144x^2y^2-16.\]

Since \(D(0,0)=-16<0\) we conclude that \((0,0)\) is a saddle point.

Furthermore, we have: \(D(-1,-1)=128>0\) and \(f_{xx}(-1,-1)=12>0\) which implies that \(f(-1,-1)=-1\) is a local minimum value.

Finally, we have: \(D(1,1)=128>0\) and \(f_{xx}(1,1)=12>0\) which implies that \(f(1,1)=-1\) is also a local minimum value.

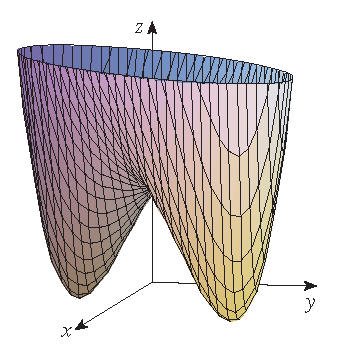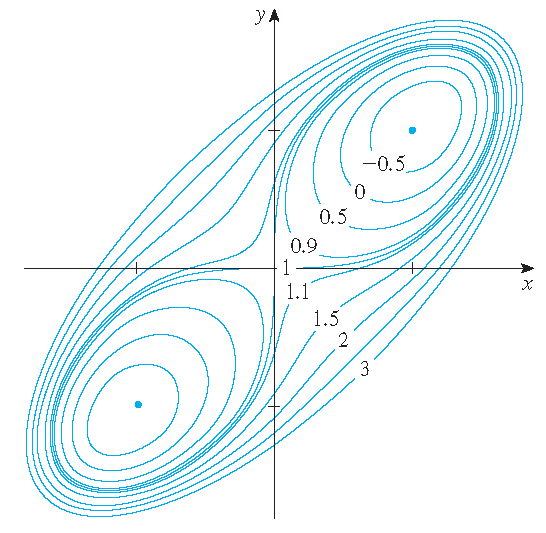Graph of \(f(x,y)=x^4+y^4-4xy+1\)	Contour map of \(f(x,y)=x^4+y^4-4xy+1\)

3) Compare with Stewart §14.7, Example 5
Find the shortest distance from the point \((1,0,-3)\) to the plane \(x+2y+z=4\).

Solution: The distance from any point \((x,y,z)\) to the point \((1,0,-3)\) is \(\sqrt{(x-1)^2+y^2+(z+3)^2}\). If \((x,y,z)\) lies on the plane \(x+2y+z=4\), then we have: \(z=4-x-2y\). So, we look for a minimum value of \(\sqrt{(x-1)^2+y^2+(7-x-2y)^2}\). Therefore, we might look for a minimum of \(f(x,y)=(x-1)^2+y^2+(7-x-2y)^2\). Looking for critical points we find

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad2(x-1)-2(7-x-2y)=0\quad\Longleftrightarrow\quad4x+4y-16=0\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad2y-4(7-x-2y)=0\quad\Longleftrightarrow\quad4x+10y-28=0.\end{array}\right.\]

Subtracting the equations we obtain \(6y-12=0\) and therefore \(y=2\) which implies that \(x=2\). Hence: \((2,2)\) is the only critical point of \(f\). Since \(f_{xx}=4\), \(f_{yy}=10\) and \(f_{xy}=4\), we have: \(D(x,y)=f_{xx}f_{yy}-\{f_{xy}\}^2=40-16=24>0\) and \(f_{xx}>0\), which implies that \(f(2,2)=1+4+1=6\) is a local minimum value of \(f\). We conclude that the shortest distance from the point \((1,0,-3)\) to the plane \(x+2y+z=4\) is \(\sqrt{6}\).

Applications:

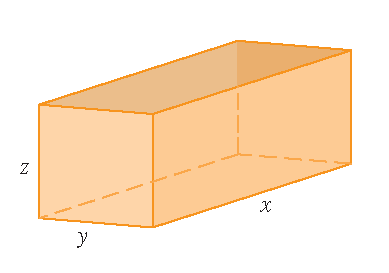1) Stewart §14.7, Example 6
A rectangular box without a lid is to be made from \(12\,\text{m}^2\) cardboard. Find the maximum volume of such a box.

Solution: Note that the volume of the box is \(V=xyz\).

The total area of the four sides and the bottom should be \(12\,\text{m}^2\).

Hence we should have: \(2xz+2yz+xy=12\).

Hence: \(2(x+y)z=12-xy\) which leads to \(z=\displaystyle\frac{12-xy}{2(x+y)}\).

This implies that the volume \(V\) is a function of two variables: \(V(x,y)=\displaystyle\frac{xy(12-xy)}{2(x+y)}\).

The partial derivatives are: \(V_x(x,y)=\displaystyle\frac{y^2(12-2xy-x^2)}{2(x+y)^2}\) and \(V_y(x,y)=\displaystyle\frac{x^2(12-2xy-y^2)}{2(x+y)^2}\).

For the maximal volume both should be equal to zero.

Since \(x\) and \(y\) should be positive, we conclude that \(12-2xy-x^2=0\) and \(12-2xy-y^2=0\).

This implies that \(y=x\) and \(12-2x^2-x^2=0\), so: \(x=y=2\) and \(z=\displaystyle\frac{12-xy}{2(x+y)}=1\).

We conclude that the maximum volume is \(V=2\cdot2\cdot1=4\,\text{m}^2\).

2) A rectangular box with a lid is to be made from \(24\,\text{m}^2\) cardboard. Find the maximum volume of such a box.

Solution: Note that the volume of the box is \(V=xyz\) with \(2xz+2yz+2xy=24\).

This leads to \(z=\displaystyle\frac{24-2xy}{2(x+y)}=\frac{12-xy}{x+y}\) and \(V(x,y)=\displaystyle\frac{xy(12-xy)}{x+y}\) with partial derivatives

\(V_x(x,y)=\displaystyle\frac{y^2(12-2xy-x^2)}{(x+y)^2}\) and \(V_y(x,y)=\displaystyle\frac{x^2(12-2xy-y^2)}{(x+y)^2}\).

For the maximal volume both should be equal to zero.

Since \(x\) and \(y\) should be positive, we conclude that \(12-2xy-x^2=0\) and \(12-2xy-y^2=0\).

This implies that \(y=x\) and \(12-2x^2-x^2=0\), so: \(x=y=2\) and \(z=\displaystyle\frac{12-xy}{x+y}=2\).

We conclude that the maximum volume is \(V=2\cdot2\cdot2=8\,\text{m}^2\).

---

Last modified on September 23, 2021