Calculus – Functions of several variables – Absolute maximum and minimum values

Definition: A function \(f\) of two variables has an absolute maximum at \((a,b)\) if \(f(x,y)\leq f(a,b)\) for all points \((x,y)\) in the domain of \(f\). The number \(f(a,b)\) is called the absolute maximum value of \(f\).

Similarly for the absolute minimum value.

Definition: A closed set in \(\mathbb{R}^2\) is one that contains all its boundary points.

Definition: A bounded set in \(\mathbb{R}^2\) is one that is contained within some disk.

Theorem: If a function \(f\) of two variables is continuous on a closed and bounded set \(D\) in \(\mathbb{R}^2\), then \(f\) attains an absolute maximum value \(f(x_1,y_1)\) and an absolute minimum value \(f(x_2,y_2)\) at some points \((x_1,y_1)\) and \((x_2,y_2)\) in \(D\).

How to find the absolute extremes of a function of two variables?

To find the absolute maximum and minimum values of a continuous function \(f\) on a closed and bounded set \(D\) in \(\mathbb{R}^2\):

1. Find the values of \(f\) at the critical points of \(f\) in \(D\);


2. Find the extreme values of \(f\) at the boundary of \(D\);


3. The largest of the values from steps 1 and 2 is the absolute maximum value of \(f\) and the smallest of these values is the absolute minimum value.

Examples:

1) Stewart §14.7, Example 7
Find the absolute maximum and minimum values of the function \(f(x,y)=x^2-2xy+2y\) on the rectangle \(D=\{(x,y)\,|\,0\leq x\leq3,\;0\leq y\leq2\}\).

Solution: For the critical points we obtain

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2x-2y=0\quad\Longleftrightarrow\quad x=y\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad -2x+2=0\quad\Longleftrightarrow\quad x=1.\end{array}\right.\]

This implies that \((1,1)\) is the only critical point of \(f\). Note that \(f(1,1)=1\).

Now we examine the four boundaries of \(D\):

1. \(0\leq x\leq 3\) and \(y=0\): \(f(x,0)=x^2=g_1(x)\) with derivative \(g_1'(x)=2x>0\). This implies that \(g_1\) is increasing; \(f(0,0)=g_1(0)=0\) is a local minimum value and \(f(3,0)=g_1(3)=9\) is a local maximum value.


2. \(x=3\) and \(0\leq y\leq 2\): \(f(3,y)=9-4y=h_1(y)\) with derivative \(h_1'(y)=-4<0\). This implies that \(h_1\) is decreasing; \(f(3,0)=h_1(0)=9\) is a local maximum value and \(f(3,2)=h_1(2)=1\) is a local minimum value.


3. \(0\leq x\leq 3\) and \(y=2\): \(f(x,2)=x^2-4x+4=(x-2)^2=g_2(x)\) with derivative \(g_2'(x)=2(x-2)\) which is positive for \(x>2\) and negative for \(x<2\). So: \(f(0,2)=g_2(0)=4\) is a local maximum value, \(f(2,2)=g_2(2)=0\) is a local minimum value and \(f(3,2)=g_2(3)=1\) is a local maximum value.


4. \(x=0\) and \(0\leq y\leq 2\): \(f(0,y)=2y=h_2(y)\) with derivative \(h_2'(y)=2>0\). This implies that \(h_2\) is increasing; \(f(0,0)=h_2(0)=0\) is a local minimum value and \(f(0,2)=h_2(2)=4\) is a local maximum value.

We conclude that \(f(0,0)=f(2,2)=0\) is the absolute minimum value and \(f(3,0)=9\) is the absolute maximum value of \(f\).

2) Find the absolute and minimum values of the function \(f(x,y)=x^2+y^2-4x-y\) on the domain \(D=\{(x,y)\,|\,x^2\leq y\leq 4\}\).

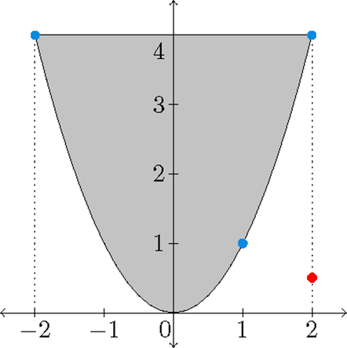
Solution: For the critical points we obtain:

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2x-4=0\quad\Longleftrightarrow\quad x=2\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad 2y-1=0\quad\Longleftrightarrow\quad y=\frac{1}{2}.\end{array}\right.\]

This implies that \((2,\frac{1}{2})\) is the only critical point of \(f\), which lies outside the domain of \(f\).

Now we examine the two boundaries of \(D\):

1. \(-2\leq x\leq 2\) and \(y=4\): \(f(x,4)=x^2-4x+12=g(x)\) with derivative \(g'(x)=2x-4\leq0\). This implies that \(f(-2,4)=g(-2)=24\) is a local maximum value and \(f(2,4)=g(2)=8\) is a local minimum value.


2. \(-2\leq x\leq 2\) and \(y=x^2\): \(f(x,x^2)=x^4-4x=h(x)\) with derivative \(h'(x)=4x^3-4\) which is positive for \(x>1\) and negative for \(x<1\). So: \(f(-2,4)=h(-2)=24\) is a local maximum value, \(f(1,1)=h(1)=-3\) is a local minimum value and \(f(2,4)=h(2)=8\) is a local maximum value.

We conclude that \(f(1,1)=-3\) is the absolute minimum value and \(f(-2,4)=24\) is the absolute maximum value of \(f\).

3) Find the absolute and minimum values of the function \(f(x,y)=2x-2y-x^2-y^2\) on the domain \(D=\{(x,y)\,|\,x^2+y^2\leq 4\}\).

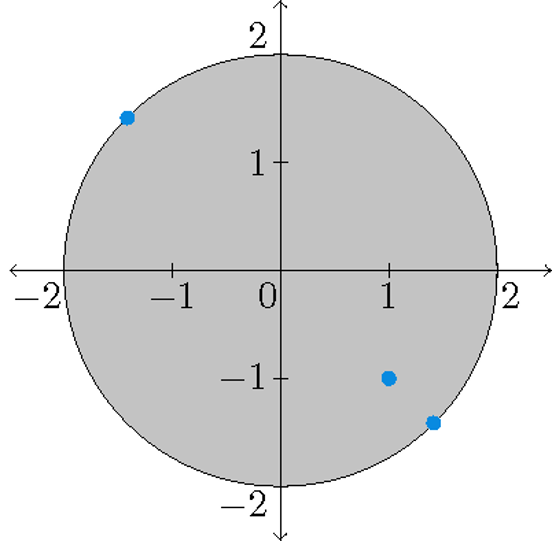
Solution: For the critical points we obtain:

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2-2x=0\quad\Longleftrightarrow\quad x=1\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad -2-2y=0\quad\Longleftrightarrow\quad y=-1.\end{array}\right.\]

This implies that \((1,-1)\) is the only critical point of \(f\), which lies inside the domain of \(f\). Note that \(f(1,-1)=2\).

On the boundary of \(D\) we take: \(x=2\cos(t)\) and \(y=2\sin(t)\) with \(0\leq t\leq2\pi\). Hence: \(f(2\cos(t),2\sin(t))=4\cos(t)-4\sin(t)-4=g(t)\) with derivative \(g'(t)=-4\sin(t)-4\cos(t)\). This equals zero for \(x=\frac{3}{4}\pi\) and for \(x=\frac{7}{4}\pi\).

Hence: \(g(\frac{3}{4}\pi)=f(-\sqrt{2},\sqrt{2})=-4\sqrt{2}-4\) is a local minimum value and \(g(\frac{7}{4}\pi)=f(\sqrt{2},-\sqrt{2})=4\sqrt{2}-4\) is a local maximum value on the boundary of \(D\). Note that \(4\sqrt{2}-4<2\).

Conclusion: the absolute minimum value of \(f\) is \(-4\sqrt{2}-4\) which is attained at \((-\sqrt{2},\sqrt{2})\) and \(2\) is the absolute maximum value of \(f\) which is attained at \((1,-1)\).

---

Last modified on September 24, 2021