Calculus – Functions of several variables – Tangent planes and linear approximations

From tangent line to tangent plane

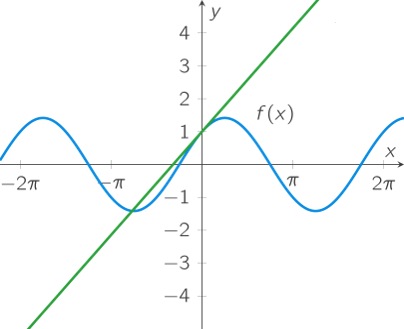
If \(y=f(x)\), then the tangent line to the graph of \(f\) through \((a,f(a))\) can be written as: \(y-f(a)=r(x-a)\) with \(r=\displaystyle\frac{dy}{dx}\bigg|_{x=a}=f'(a)\). Hence: \(y=f(a)+f'(a)(x-a)\). The function \(L(x)=f(a)+f'(a)(x-a)\) is called the linearization of \(f\) at the point \(a\).

Definition: The tangent plane to the graph of a function \(f\) of two variables at the point \(P\) is the plane through the tnagnet lines \(T_1\) and \(T_2\) to any two curves \(\mathcal{C}_1\) and \(\mathcal{C}_2\) through \(P\) on the surface \(z=f(x,y)\).

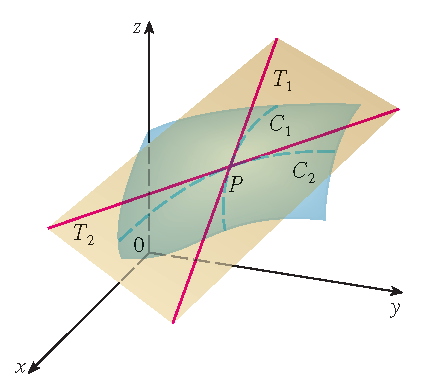
Theorem: Suppose that \(f\) has continuous partial derivatives. An equation of the tangent plane to the surface \(z=f(x,y)\), the graph of \(f\), at the point \((a,b,f(a,b))\) is

\[z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b).\]

Definition: The function

\[L(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\]

is called the linearization of \(f\) at the point \((a,b)\).

Differentiability

Definition: A function \(f\) of two variables is called differentiable at the point \((a,b)\) if

\[\lim\limits_{(x,y)\to(a,b)}\frac{f(x,y)-L(x,y)}{\sqrt{(x-a)^2+(y-b)^2}}=0.\]

Theorem: If the partial derivatives \(f_x\) and \(f_y\) exist near \((a,b)\) and are continuous at \((a,b)\), then \(f\) is differentiable at \((a,b)\).

Example: The function \(f(x,y)=\displaystyle\left\{\begin{array}{ll}\displaystyle\frac{xy}{x^2+y^2},&(x,y)\neq(0,0)\\[2.5mm] 0,&(x,y)=(0,0)\end{array}\right.\) is not differentiable at \((0,0)\).

Differentials

Definition: For a differentiable function \(f\) of two variables, \(z=f(x,y)\), we define the differentials \(dx\) and \(dy\) to be independent variables. Then the (total) differential \(dz\) is defined by

\[dz=f_x(x,y)\,dx+f_y(x,y)\,dy.\]

Applications:

1) We want to paint the border of this swimming pool with dimensions \(10\times5\) meters.

In order to buy the right amount of paint, we use differentials to approximate the (total) area of the border, which has a width of \(20\) cm.

Let \(x=10\) (the length) and \(y=5\) (the width), then the area of the pool is \(A(x,y)=xy\). Then we have:

\[dA=\frac{\partial A}{\partial x}\,dx+\frac{\partial A}{\partial y}\,dy=y\,dx+x\,dy.\]

This implies: \(dA=5\cdot(0.4)+10\cdot(0.4)=6\,\text{m}^2\).

Compare with: Stewart, §14.4, Exercise 33.

2) Consider a tin can with a circular bottom and lid with radius \(r\) and height \(h\).

Then the volume equals: \(V=\pi r^2h\).

Now take for instance: \(r=5\) and \(h=10\).

Then we have: \(V=\pi\cdot25\cdot10=250\pi\).

Now suppose that \(dr=0.1\) and \(dh=0.2\) (for instance).

Then we have:

\[dV=\frac{\partial V}{\partial r}\,dr+\frac{\partial V}{\partial h}\,dh=2\pi rh\,dr+\pi r^2\,dh=100\pi\cdot0.1+25\pi\cdot0.2=10\pi+5\pi=15\pi.\]

This is an estimate of the absolute (maximal) error \(\Delta V\).

The relative (maximal) error is: \(\displaystyle\frac{\Delta V}{V}\approx\frac{dV}{V}=\frac{15\pi}{250\pi}=\frac{3}{50}\;(6\,\%)\).

Compare with: Stewart, §14.4, Execises 34 and 35.

3) Stewart, §14.4, Exercise 41
Previously, the Body Mass Index (BMI) of a person was defined as

\[B(m,h)=\frac{m}{h^2},\]

where \(m\) is the person's mass (in kilograms) and \(h\) its height (in meters).

The partial derivatives are

\[B_m(m,h)=\frac{1}{h^2}\quad\text{and}\quad B_h(m,h)=-\frac{2m}{h^3}.\]

So: the linear approximation of \(B(m,h)\) for a child with mass \(23\) kg and height \(1.10\) m is

\[L(m,h)=B(23,1.1)+B_m(23,1.1)(m-23)+B_h(23,1.1)(h-1.1)\approx19+0.8264(m-23)-34.5605(h-1.1).\]

If the child's mass increases by \(1\) kg and its height by \(3\) cm, then this linear approximation implies for the BMI:

\[L(24,1.13)\approx19+0.8264\cdot1−34.5605\cdot0.03\approx18.8.\]

Note that the actual BMI equals: \(B(24,1.13)=\displaystyle\frac{24}{(1.13)^2}\approx18.8\).

---

Last modified on September 16, 2021