Analyse – Functies van meerdere variabelen – Globale maxima en minima

Definitie: Een functie \(f\) van twee variabelen heeft een globaal maximum in \((a,b)\) als \(f(x,y)\leq f(a,b)\) voor alle punten \((x,y)\) in het domein van \(f\). Het getal \(f(a,b)\) heet het globaal maximum van \(f\).

Evenzo voor het globaal minimum.

Definitie: Een gesloten verzameling in \(\mathbb{R}^2\) is een verzameling die al haar randpunten bevat.

Definitie: Een begrensde verzameling in \(\mathbb{R}^2\) is een verzameling die binnen een cirkelschijf ligt.

Stelling: Als een functie \(f\) van twee variabelen continu is op een gesloten en begrensde verzameling \(D\) in \(\mathbb{R}^2\), dan neemt \(f\) een globaal maximum \(f(x_1,y_1)\) en een globaal minimum \(f(x_2,y_2)\) aan in zekere punten \((x_1,y_1)\) en \((x_2,y_2)\) in \(D\).

Hoe vinden we de globale extremen van een functie van twee variabelen?

Om het globale maximum en minimum van een continue functie \(f\) op een gesloten en begrensde verzameling \(D\) in \(\mathbb{R}^2\) te bepalen:

1. Bepaal de waarden van \(f\) in de kritieke punten van \(f\) in \(D\);


2. Bepaal de extreme waarden van \(f\) op de rand van \(D\);


3. De grootste van de waarden uit stap 1 en 2 is het globale maximum van \(f\) en de kleinste van deze waarden is het globale minimum.

Voorbeelden:

1) Stewart §14.7, Voorbeeld 7
Bepaal het globale maximum en minimum van de functie \(f(x,y)=x^2-2xy+2y\) op de rechthoek \(D=\{(x,y)\,|\,0\leq x\leq3,\;0\leq y\leq2\}\).

Oplossing: Voor de kritieke punten geldt:

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2x-2y=0\quad\Longleftrightarrow\quad x=y\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad -2x+2=0\quad\Longleftrightarrow\quad x=1.\end{array}\right.\]

Hieruit volgt dat \((1,1)\) het enige kritieke punt van \(f\) is. Merk op dat \(f(1,1)=1\).

Nu onderzoeken we de vier randen van \(D\):

1. \(0\leq x\leq 3\) en \(y=0\): \(f(x,0)=x^2=g_1(x)\) met afgeleide \(g_1'(x)=2x>0\). Hieruit volgt dat \(g_1\) stijgend is; \(f(0,0)=g_1(0)=0\) is een lokaal minimum en \(f(3,0)=g_1(3)=9\) is een lokaal maximum.


2. \(x=3\) en \(0\leq y\leq 2\): \(f(3,y)=9-4y=h_1(y)\) met afgeleide \(h_1'(y)=-4<0\). Hieruit volgt dat \(h_1\) dalend is; \(f(3,0)=h_1(0)=9\) is een lokaal maximum en \(f(3,2)=h_1(2)=1\) is een lokaal minimum.


3. \(0\leq x\leq 3\) en \(y=2\): \(f(x,2)=x^2-4x+4=(x-2)^2=g_2(x)\) met afgeleide \(g_2'(x)=2(x-2)\), die positief is voor \(x>2\) en negatief voor \(x<2\). Dus: \(f(0,2)=g_2(0)=4\) is een lokaal maximum, \(f(2,2)=g_2(2)=0\) is een lokaal minimum en \(f(3,2)=g_2(3)=1\) is een lokaal maximum.


4. \(x=0\) en \(0\leq y\leq 2\): \(f(0,y)=2y=h_2(y)\) met afgeleide \(h_2'(y)=2>0\). Hieruit volgt dat \(h_2\) stijdend is; \(f(0,0)=h_2(0)=0\) is een lokaal minimum en \(f(0,2)=h_2(2)=4\) is een lokaal maximum.

We concluderen dat \(f(0,0)=f(2,2)=0\) het globale minimum en dat \(f(3,0)=9\) het globale maximum van \(f\) is.

2) Bepaal het globale maximum en minimum van de functie \(f(x,y)=x^2+y^2-4x-y\) op het domein \(D=\{(x,y)\,|\,x^2\leq y\leq 4\}\).

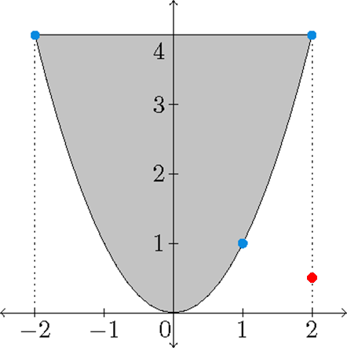
Oplossing: Voor de kritieke punten geldt:

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2x-4=0\quad\Longleftrightarrow\quad x=2\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad 2y-1=0\quad\Longleftrightarrow\quad y=\frac{1}{2}.\end{array}\right.\]

Hieruit volgt dat \((2,\frac{1}{2})\) het enige kritieke punt van \(f\) is, dat buiten het domein van \(f\) ligt.

Nu onderzoeken we de twee randen van \(D\):

1. \(-2\leq x\leq 2\) en \(y=4\): \(f(x,4)=x^2-4x+12=g(x)\) met afgeleide \(g'(x)=2x-4\leq0\). Hieruit volgt dat \(f(-2,4)=g(-2)=24\) een lokaal maximum is en dat \(f(2,4)=g(2)=8\) een lokaal minimum is.


2. \(-2\leq x\leq 2\) en \(y=x^2\): \(f(x,x^2)=x^4-4x=h(x)\) met afgeleide \(h'(x)=4x^3-4\) die positief is voor \(x>1\) en negatief voor \(x<1\). Dus: \(f(-2,4)=h(-2)=24\) is een lokaal maximum, \(f(1,1)=h(1)=-3\) is een lokaal minimum en \(f(2,4)=h(2)=8\) is een lokaal maximum.

We concluderen dat \(f(1,1)=-3\) het globale minimum en dat \(f(-2,4)=24\) het globale maximum van \(f\) is.

3) Bepaal het globale maximum en minimum van de functie \(f(x,y)=2x-2y-x^2-y^2\) op het domein \(D=\{(x,y)\,|\,x^2+y^2\leq 4\}\).

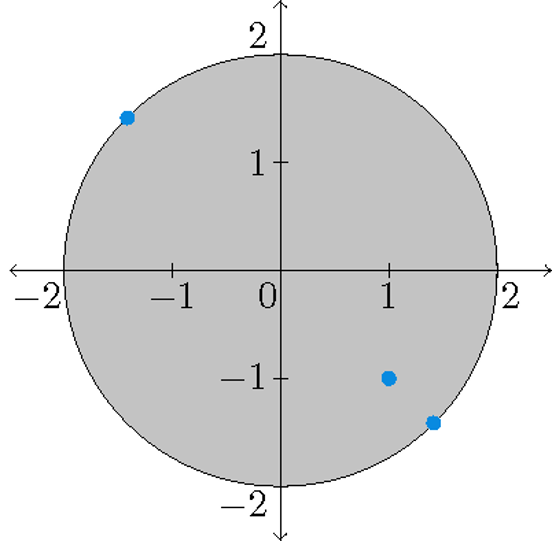
Oplossing: Voor de kritieke punten geldt:

\[\left\{\begin{array}{l}f_x(x,y)=0\quad\Longleftrightarrow\quad 2-2x=0\quad\Longleftrightarrow\quad x=1\\[2.5mm] f_y(x,y)=0\quad\Longleftrightarrow\quad -2-2y=0\quad\Longleftrightarrow\quad y=-1.\end{array}\right.\]

Hieruit volgt dat \((1,-1)\) het enige kritieke punt van \(f\) is, dat binnen het domein van \(f\) ligt. Merk op dat \(f(1,-1)=2\).

Op de rand van \(D\) nemen we: \(x=2\cos(t)\) en \(y=2\sin(t)\) met \(0\leq t\leq2\pi\). Dus: \(f(2\cos(t),2\sin(t))=4\cos(t)-4\sin(t)-4=g(t)\) met afgeleide \(g'(t)=-4\sin(t)-4\cos(t)\). Dit is gelijk aan nul voor \(x=\frac{3}{4}\pi\) en voor \(x=\frac{7}{4}\pi\).

Dus: \(g(\frac{3}{4}\pi)=f(-\sqrt{2},\sqrt{2})=-4\sqrt{2}-4\) is een lokaal minimum en \(g(\frac{7}{4}\pi)=f(\sqrt{2},-\sqrt{2})=4\sqrt{2}-4\) is een lokaal maximum op de rand van \(D\). Merk op dat \(4\sqrt{2}-4<2\).

Conclusie: het globale minimum van \(f\) is \(-4\sqrt{2}-4\) en dat wordt aangenomen in \((-\sqrt{2},\sqrt{2})\) en \(2\) is het globale maximum van \(f\) en dat wordt aangenomen in \((1,-1)\).

---

Laatst gewijzigd op 24 september 2021