Analyse – Functies van meerdere variabelen – Partiële afgeleiden

Definitie: Laat \(f\) een functie zijn van twee variabelen. Dan heet

\[f_x(a,b)=\lim\limits_{h\to0}\frac{f(a+h,b)-f(a,b)}{h}\]

de partiële afgeleide van \(f\) naar \(x\) in het punt \((a,b)\) en heet

\[f_y(a,b)=\lim\limits_{h\to0}\frac{f(a,b+h)-f(a,b)}{h}\]

de partiële afgeleide van \(f\) naar \(y\) in het punt \((a,b)\).

Algemener: \(f_x(x,y)=\displaystyle\lim\limits_{h\to0}\frac{f(x+h,y)-f(x,y)}{h}\) en \(f_y(x,y)=\displaystyle\lim\limits_{h\to0}\frac{f(x,y+h)-f(x,y)}{h}\).

We gebruiken de notaties

\[f_x(x,y)=f_x=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)\quad\text{en}\quad f_y(x,y)=f_y=\frac{\partial f}{\partial y}=\frac{\partial}{\partial y}f(x,y).\]

Meer dan twee variabelen

Voor een functie \(f\) van drie variabelen geldt: \(f_x(x,y,z)=\displaystyle\lim\limits_{h\to0}\frac{f(x+h,y,z)-f(x,y,z)}{h}\), \(f_y(x,y,z)=\displaystyle\lim\limits_{h\to0}\frac{f(x,y+h,z)-f(x,y,z)}{h}\) en \(f_z(x,y,z)=\displaystyle\lim\limits_{h\to0}\frac{f(x,y,z+h)-f(x,y,z)}{h}\). Evenzo in het geval van meer variabelen.

Hogere orde partiële afgeleiden

\begin{align*} f_{xx}&=(f_x)_x=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2f}{\partial x^2}\\[2.5mm] f_{xy}&=(f_x)_y=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2f}{\partial y\partial x}\\[2.5mm] f_{yx}&=(f_y)_x=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial x\partial y}\\[2.5mm] f_{yy}&=(f_y)_y=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial y^2} \end{align*}

Voorbeeld: Als \(f(x,y)=e^{2x+y}\ln(x^2+3y^2)\), dan geldt

\[f_x(x,y)=2e^{2x+y}\ln(x^2+3y^2)+e^{2x+y}\frac{2x}{x^2+3y^2}\quad\text{en}\quad f_y(x,y)=e^{2x+y}\ln(x^2+3y^2)+e^{2x+y}\frac{6y}{x^2+3y^2}.\]

Verder geldt

\[f_{xy}(x,y)=2e^{2x+y}\ln(x^2+3y^2)+2e^{2x+y}\frac{6y}{x^2+3y^2}+e^{2x+y}\frac{2x}{x^2+3y^2}-e^{2x+y}\frac{12xy}{(x^2+3y^2)^2}\]

en

\[f_{yx}(x,y)=2e^{2x+y}\ln(x^2+3y^2)+e^{2x+y}\frac{2x}{x^2+3y^2}+2e^{2x+y}\frac{6y}{x^2+3y^2}-e^{2x+y}\frac{12xy}{(x^2+3y^2)^2}.\]

Merk op dat deze gelijk zijn en dat is geen toeval.

De stelling van Clairaut

Stelling: Neem aan dat \(f\) is gedefinieerd op een cirkelschijf \(D\) dat het punt \((a,b)\) bevat. Als de functies \(f_{xy}\) en \(f_{yx}\) beide continu zijn op \(D\), dan geldt:

\[f_{xy}(a,b)=f_{yx}(a,b).\]

Bewijs: Zie Stewart, Appendix F.

Partiële differentiaalvergelijkingen

Definitie: Een partiële differentiaalvergelijking is een vergelijking in een onbekende functie van meerdere variabelen en één of meer van haar partiële afgeleiden.

Voorbeelden zijn

1. de warmte- of diffusievergelijking \(\alpha^2u_{xx}=u_t\) waarbij \(\alpha^2\) een positieve constante (de diffusieconstante) is;


2. de golfvergelijking \(a^2u_{xx}=u_{tt}\), waarbij \(a^2\) een positieve constante (dhe veerconstante) is;


3. de Laplace of potentiaalvergelijking \(u_{xx}+u_{yy}=0\).

Voorbeelden

1) De functie \(u(x,y)=e^{-x}\cos(y)\) is een oplossing van de Laplace of potentiaalvergelijking \(u_{xx}+u_{yy}=0\), want:

\[\left\{\begin{array}{l}u_x(x,y)=-e^{-x}\cos(y)\quad\Longrightarrow\quad u_{xx}(x,y)=e^{-x}\cos(y)\\[2.5mm] u_y(x,y)=-e^{-x}\sin(y)\quad\Longrightarrow\quad u_{yy}(x,y)=-e^{-x}\cos(y),\end{array}\right.\]

waaruit volgt dat \(u_{xx}+u_{yy}=0\).

2) De functie \(u(x,t)=\sin(x+at)\) is een oplossing van de golfvergelijking \(a^2u_{xx}=u_{tt}\), want:

\[\left\{\begin{array}{l}u_x(x,t)=\cos(x+at)\quad\Longrightarrow\quad u_{xx}(x,t)=-\sin(x+at)\\[2.5mm] u_t(x,t)=a\cos(x+at)\quad\Longrightarrow\quad u_{tt}(x,t)=-a^2\sin(x+at),\end{array}\right.\]

waaruit volgt dat \(a^2u_{xx}=u_{tt}\).

Toepassing:

Stewart §14.3: Voorbeeld 3
De Body Mass Index (BMI) of Quetelet Index (QI) van een persoon wordt gedefinieerd door

\[B(m,h)=\frac{m}{h^2},\]

waarbij \(m\) de massa (in kilogrammen) van de persoon is en \(h\) de lengte (in meters).

De partiële afgeleiden van \(B\) naar \(m\) en \(h\) zijn: \(\displaystyle\frac{\partial B}{\partial m}=\frac{1}{h^2}\) en \(\displaystyle\frac{\partial B}{\partial h}=-\frac{2m}{h^3}\).

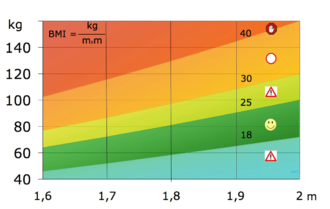
Bijvoorbeeld:

\[B_m(64,1.68)=\frac{1}{(1.68)^2}\approx0.35\quad\text{en}\quad B_h(64,1.68)=-\frac{2\cdot64}{(1.68)^3}\approx-27.\]

Dus, voor een persoon met een lengte van \(1.68\) m en een massa van \(64\) kg geldt:

Als de massa een klein beetje toeneemt, zeg met \(1\) kg, en de lengte blijft gelijk, dan zal de BMI toenemen met ongeveer \(0.35\).

Als de lengte een klein beetje toeneemt, zeg met \(1\) cm, en de massa blijft gelijk, dan zal de BMI afnemen met ongeveer \(0.27\).

---

Laatst gewijzigd op 15 september 2021