Calculus – Differentiation – Implicit differentiation

Stewart §3.5, Example 1

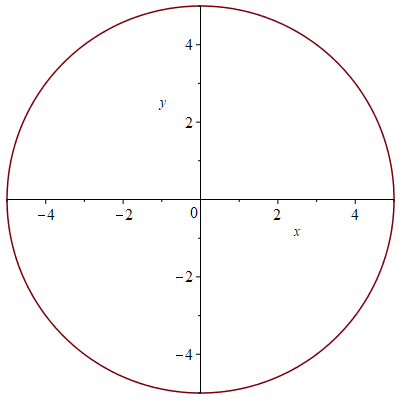
Consider the circle given by \(x^2+y^2=25\).

1. Find \(\displaystyle\frac{dy}{dx}\).


2. Find an equation of the tangent line to the circle at the point \((3,4)\).


3. Find an equation of the tangent line to the circle at the point \((-4,-3)\).

Solution:
If we solve \(x^2+y^2=25\) explicitly for \(y\) we obtain: \(y=\pm\sqrt{25-x^2}\). So we have to distinguish between two functions.

Using implicit differentiation we simply find that

\[x^2+y^2=25\quad\Longrightarrow\quad 2x+2y\cdot\frac{dy}{dx}=0\]

which implies that \(\displaystyle\frac{dy}{dx}=-\frac{2x}{2y}=-\frac{x}{y}\). Note that at the points \((-5,0)\) and \((5,0)\) where \(y=0\) the tangent line is vertical.

At the point \((3,4)\) this reads \(\displaystyle\frac{dy}{dx}=-\frac{3}{4}\).

An equation of the tangent line to the circle at the point \((3,4)\) is therefore

\[y-4=-\frac{3}{4}(x-3)\quad\text{or}\quad 3x+4y=25.\]

At the point \((-4,-3)\) this reads \(\displaystyle\frac{dy}{dx}=-\frac{4}{3}\).

An equation of the tangent line to the circle at the point \((-4,-3)\) is therefore

\[y+3=-\frac{4}{3}(x+4)\quad\text{or}\quad 4x+3y=-25.\]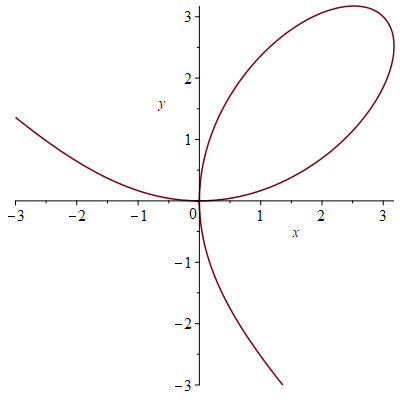

Stewart §3.5, Example 2

Consider the folium of Descartes given by \(x^3+y^3=6xy\).

1. Find \(\displaystyle\frac{dy}{dx}\).


2. Find an equation of the tangent line to the folium of Descartes at the point \((3,3)\).


3. Find the point in the first quadrant at which the tangent line is horizontal.


4. Find the point in the first quadrant at which the tangent line is vertical.

Solution:
Using implicit differentiation we find that

\[x^3+y^3=6xy\quad\Longrightarrow\quad 3x^2+3y^2\cdot\frac{dy}{dx}=6y+6x\cdot\frac{dy}{dx}\]

which implies that \(\displaystyle(3y^2-6x)\frac{dy}{dx}=6y-3x^2\) or \(\displaystyle(y^2-2x)\frac{dy}{dx}=2y-x^2\).

So, for \(y^2-2x\neq0\) we conclude that \(\displaystyle\frac{dy}{dx}=\frac{2y-x^2}{y^2-2x}\).

At the point \((3,3)\) this reads \(\displaystyle\frac{dy}{dx}=\frac{6-9}{9-6}=-1\).

An equation of the tangent line to the folium of Descartes at the point \((3,3)\) is therefore

\[y-3=-(x-3)\quad\text{or}\quad x+y=6.\]

For a horizontal tangent line we need that \(\displaystyle\frac{dy}{dx}=0\) which implies that \(2y-x^2=0\) and \(y^2-2x\neq0\).

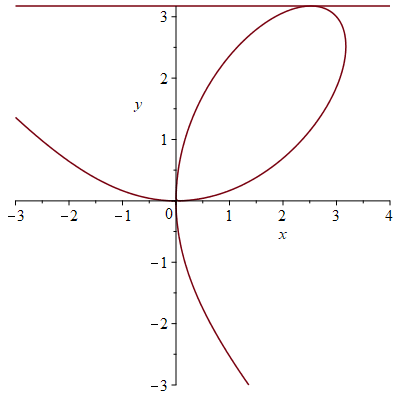Substituting \(y=\frac{1}{2}x^2\) into \(x^3+y^3=6xy\) we obtain:

\[x^3+\frac{1}{8}x^6=3x^3\quad\Longleftrightarrow\quad x^6=16x^3.\]

Since \(x\neq0\) in the first quadrant, we conclude that \(x^3=16\) or \(x=\sqrt[3]{16}=2\sqrt[3]{2}\) which implies that \(y=\frac{1}{2}x^2=2\sqrt[3]{4}\).

Hence: the tangent line is horizontal at the point \((2\sqrt[3]{2},2\sqrt[3]{4})\).

Note that for a vertical tangent line we need that \(y^2-2x=0\) and \(2y-x^2\neq0\).

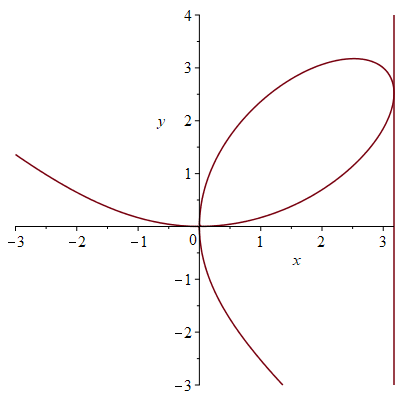Substituting \(x=\frac{1}{2}y^2\) into \(x^3+y^3=6xy\) we obtain:

\[\frac{1}{8}y^6+y^3=3y^3\quad\Longleftrightarrow\quad y^6=16y^3.\]

Since \(y\neq0\) in the first quadrant, we conclude that \(y^3=16\) or \(y=\sqrt[3]{16}=2\sqrt[3]{2}\) which implies that \(x=\frac{1}{2}y^2=2\sqrt[3]{4}\).

Hence: the tangent line is vertical at the point \((2\sqrt[3]{4},2\sqrt[3]{2})\). Note that we could have used the symmetry as well.

The lamp and the shadow

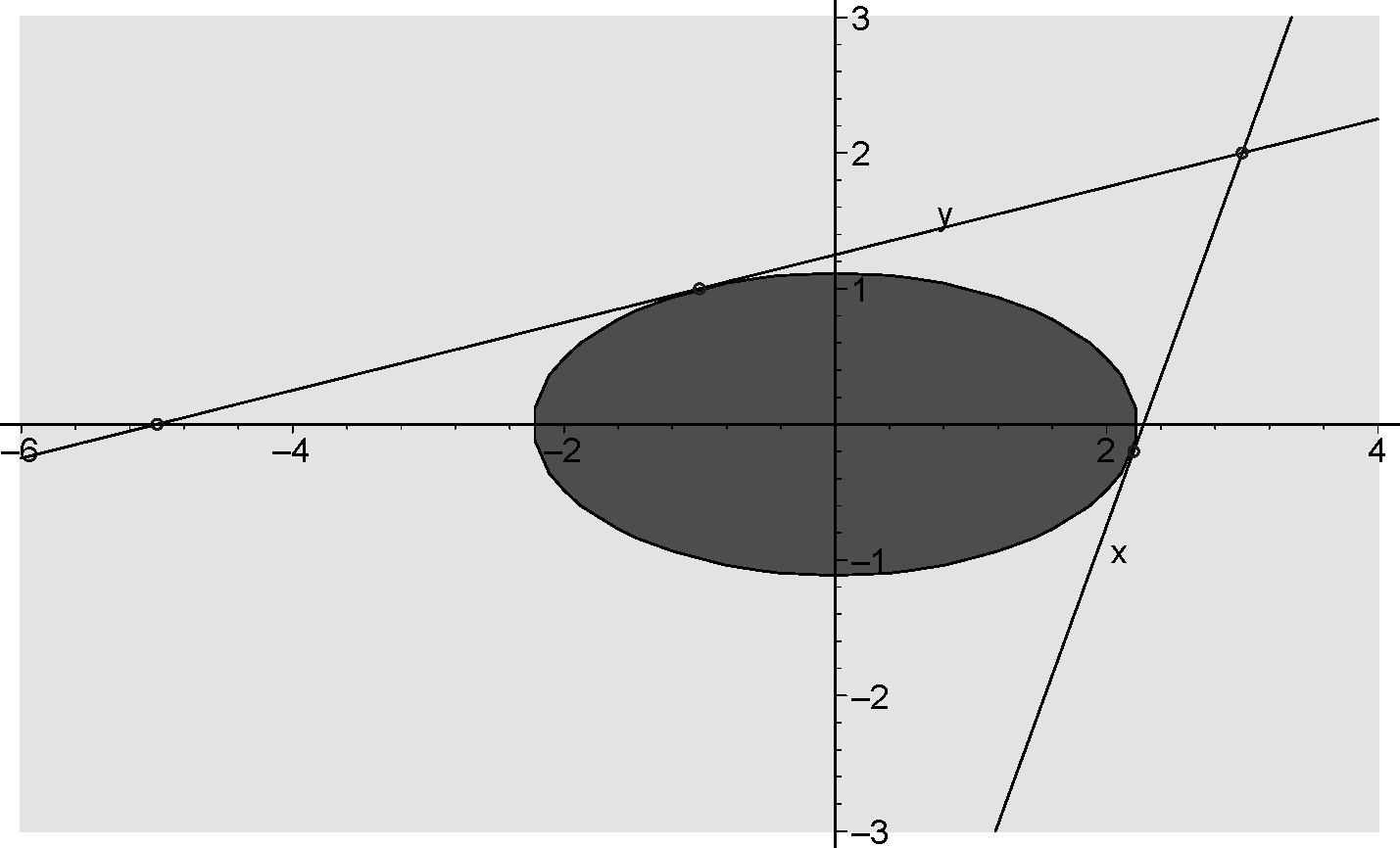Stewart §3.5, Exercise 80

Consider the elliptical region given by \(x^2+4y^2\leq5\).

Find the height \(h\) of the lamp located at \(x=3\).

Solution:
Consider the tangent line to the ellipse through the points \((-5,0)\) and \((3,h)\).

The slope of this tangent line equals \(\displaystyle\frac{h}{8}\).

If we call the point of tangency to the ellipse \((a,b)\), then this slope can also be written as: \(\displaystyle\frac{b}{a+5}\).

By means of implicit differentiation we obtain: \(2x+8y\displaystyle\frac{dy}{dx}=0\quad\Longrightarrow\quad\frac{dy}{dx}=-\frac{2x}{8y}=-\frac{x}{4y}\).

At the point \((a,b)\) this equals \(-\displaystyle\frac{a}{4b}\).

Hence we have: \(\displaystyle\frac{h}{8}=\frac{b}{a+5}=-\frac{a}{5b}\quad\Longrightarrow\quad a^2+4b^2=-5a\).

Since the point \((a,b)\) is also located on the ellipse we also have: \(a^2+5b^2=5\).

Hence we have: \(a=-1\) which implies that \(b=1\) and therefore \(\displaystyle\frac{h}{8}=\frac{1}{4}\quad\Longrightarrow\quad h=\frac{8}{4}=2\).

This implies that the height of the lamp equals \(2\).

Although this completes the solution of the exercise, it is interesting to look at it in somewhat more detail. Note that the point of tangency of the upper tangent line, through the points \((−5,0)\) and \((3,2)\), is: \((−1,1)\). Now we can also find the point of tangency of the lower tangent line to the ellipse. This tangent line also passes the point \((3,2)\) and therefore has the form:

\[y-2=r(x-3),\]

where \(r\) denotes the slope of this tangent line. This equals the derivative \(\displaystyle\frac{dy}{dx}\) at this point of tangency. Hence if we call this point \((c,d)\), then we have:

\[r=\displaystyle\frac{dy}{dx}\bigg|_{(c,d)}=-\frac{c}{4d}.\]

The point \((c,d)\) lies on the tangent line, hence we have:

\[d-2=-\displaystyle\frac{c}{4d}(c-3)\quad\Longrightarrow\quad c^2+4d^2=3c+8d.\]

Since the point \((c,d)\) also lies on the ellipse, we also have: \(c^2+4d^2=5\). Hence we have: \(3c+8d=5\).

Finally, substitution then leads to: \(c=\displaystyle\frac{11}{5}\) and \(d=-\displaystyle\frac{1}{5}\). The slope at this point equals \(\displaystyle\frac{11}{4}\).

The derivative of the Lambert \(W\) function

The Lambert \(W\) function is the inverse of the function \(y=xe^x\) with domain \([-1,\infty)\) and range \([-e^{-1},\infty)\). This implies that \(W(x)e^{W(x)}=x\).

Implicit differentiation leads to: \(W'(x)e^{W(x)}+W(x)\cdot W'(x)e^{W(x)}=1\;\Longleftrightarrow\;W'(x)\left(1+W(x)\right)e^{W(x)}=1\) for \(x>-e^{-1}\).

Hence: \(W'(x)=\displaystyle\frac{1}{\left(1+W(x)\right)e^{W(x)}}\) for \(x>-e^{-1}\). Since \(W(0)=0\), this implies that \(W'(0)=1\).

Using \(W(x)e^{W(x)}=x\) we have \(W'(x)=\displaystyle\frac{W(x)}{\left(1+W(x)\right)W(x)e^{W(x)}}=\frac{W(x)}{x\left(1+W(x)\right)}\) for \(x>-e^{-1}\) and \(x\neq0\).

---

Last modified on March 10, 2024