Analyse – Differentiëren – Impliciet differentiëren

Stewart §3.5, Voorbeeld 1

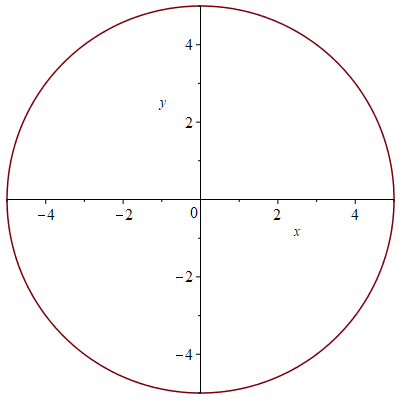
Beschouw de cirkel gegeven door \(x^2+y^2=25\).

1. Bepaal \(\displaystyle\frac{dy}{dx}\).


2. Bepaal een vergelijking van de raaklijn aan de cirkel in het punt \((3,4)\).


3. Bepaal een vergelijking van de raaklijn aan de cirkel in het punt \((-4,-3)\).

Oplossing:
Als we \(x^2+y^2=25\) expliciet oplossen voor \(y\) dan volgt: \(y=\pm\sqrt{25-x^2}\). We moeten dan dus onderscheid maken tussen twee functies.

Gebruikmakend van impliciet differentiëren volgt eenvoudig dat

\[x^2+y^2=25\quad\Longrightarrow\quad 2x+2y\cdot\frac{dy}{dx}=0\]

waaruit volgt dat \(\displaystyle\frac{dy}{dx}=-\frac{2x}{2y}=-\frac{x}{y}\). Merk op dat in de punten \((-5,0)\) en \((5,0)\) waar \(y=0\) is de raaklijn verticaal is.

In het punt \((3,4)\) geldt dat \(\displaystyle\frac{dy}{dx}=-\frac{3}{4}\).

Een vergelijking van de raaklijn aan de cirkel in het punt \((3,4)\) is dus

\[y-4=-\frac{3}{4}(x-3)\quad\text{of}\quad 3x+4y=25.\]

In het punt \((-4,-3)\) geldt dat \(\displaystyle\frac{dy}{dx}=-\frac{4}{3}\).

Een vergelijking van de raaklijn aan de cirkel in het punt \((-4,-3)\) is dus

\[y+3=-\frac{4}{3}(x+4)\quad\text{of}\quad 4x+3y=-25.\]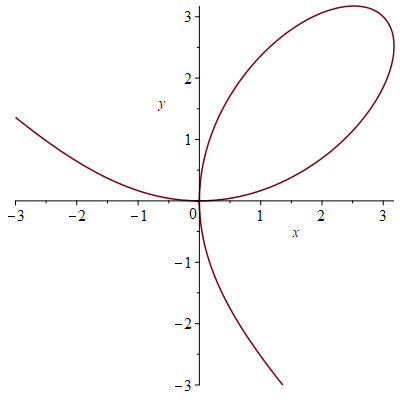

Stewart §3.5, Voorbeeld 2

Beschouw het folium van Descartes gegeven door \(x^3+y^3=6xy\).

1. Bepaal \(\displaystyle\frac{dy}{dx}\).


2. Bepaal een vergelijking van de raaklijn aan het folium van Descartes in het punt \((3,3)\).


3. Bepaal het punt in het eerste kwadrant waarin de raaklijn horizontaal is.


4. Bepaal het punt in het eerste kwadrant waarin de raaklijn verticaal is.

Oplossing:
Gebruikmakend van impliciet differentiëren volgt dat

\[x^3+y^3=6xy\quad\Longrightarrow\quad 3x^2+3y^2\cdot\frac{dy}{dx}=6y+6x\cdot\frac{dy}{dx}\]

waaruit volgt dat \(\displaystyle(3y^2-6x)\frac{dy}{dx}=6y-3x^2\) of \(\displaystyle(y^2-2x)\frac{dy}{dx}=2y-x^2\).

Dus, voor \(y^2-2x\neq0\) concluderen we dat \(\displaystyle\frac{dy}{dx}=\frac{2y-x^2}{y^2-2x}\).

In het punt \((3,3)\) geldt dat \(\displaystyle\frac{dy}{dx}=\frac{6-9}{9-6}=-1\).

Een vergelijking van de raaklijn aan het folium van Descartes in het punt \((3,3)\) is dus

\[y-3=-(x-3)\quad\text{of}\quad x+y=6.\]

Voor een horizontale raaklijn moet gelden dat \(\displaystyle\frac{dy}{dx}=0\) en dus \(2y-x^2=0\) en \(y^2-2x\neq0\).

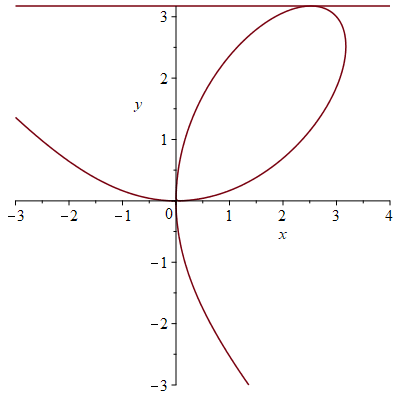Substitueren van \(y=\frac{1}{2}x^2\) in \(x^3+y^3=6xy\) geeft dan:

\[x^3+\frac{1}{8}x^6=3x^3\quad\Longleftrightarrow\quad x^6=16x^3.\]

Omdat \(x\neq0\) in het eerste kwadrant, concluderen we dat \(x^3=16\) of \(x=\sqrt[3]{16}=2\sqrt[3]{2}\) waaruit volgt dat \(y=\frac{1}{2}x^2=2\sqrt[3]{4}\).

Dus: de raaklijn is horizontaal in het punt \((2\sqrt[3]{2},2\sqrt[3]{4})\).

Merk op dat voor een verticale raaklijn moet gelden dat \(y^2-2x=0\) en \(2y-x^2\neq0\).

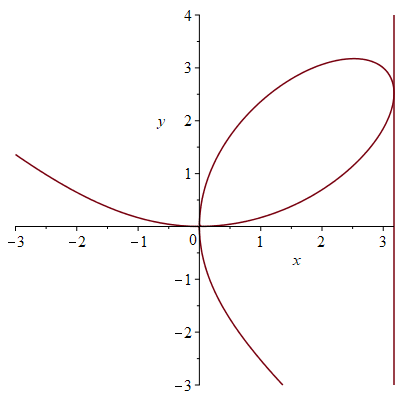Substitueren van \(x=\frac{1}{2}y^2\) into \(x^3+y^3=6xy\) geeft nu:

\[\frac{1}{8}y^6+y^3=3y^3\quad\Longleftrightarrow\quad y^6=16y^3.\]

Omdat \(y\neq0\) in het eerste kwadrant, concluderen we dat \(y^3=16\) of \(y=\sqrt[3]{16}=2\sqrt[3]{2}\) waaruit volgt dat \(x=\frac{1}{2}y^2=2\sqrt[3]{4}\).

Dus: de raaklijn is verticaal in het punt \((2\sqrt[3]{4},2\sqrt[3]{2})\). Merk op dat we ook de symmetrie hadden kunnen gebruiken.

De lamp en de schaduw

Stewart §3.5, Opgave 80

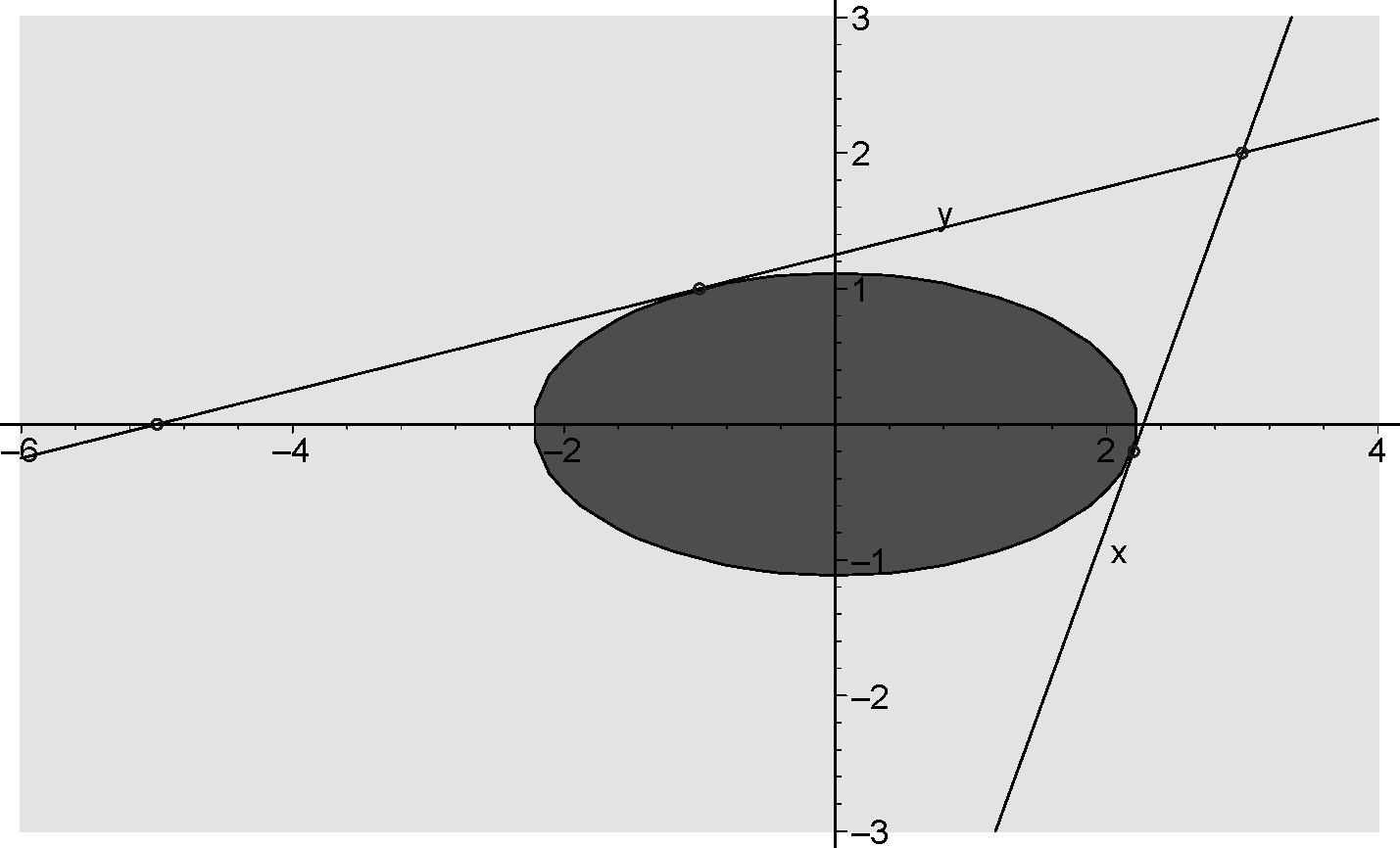
Beschouw het elliptische gebied gegeven door \(x^2+4y^2\leq5\).

Bepaal de hoogte \(h\) van de lamp op positie \(x=3\).

Oplossing:
Beschouw de raaklijn aan de ellips door de punten \((-5,0)\) en \((3,h)\).

De richtingscoëfficiënt van deze raaklijn is gelijk aan \(\displaystyle\frac{h}{8}\).

Als we het raakpunt aan de ellips \((a,b)\) noemen, dan kan deze richtingscoëfficiënt ook worden geschreven als: \(\displaystyle\frac{b}{a+5}\).

Door middel van impliciet differentiëren volgt dat: \(2x+8y\displaystyle\frac{dy}{dx}=0\quad\Longrightarrow\quad\frac{dy}{dx}=-\frac{2x}{8y}=-\frac{x}{4y}\).

In het punt \((a,b)\) is dit gelijk aan \(-\displaystyle\frac{a}{4b}\).

Dus geldt: \(\displaystyle\frac{h}{8}=\frac{b}{a+5}=-\frac{a}{5b}\quad\Longrightarrow\quad a^2+4b^2=-5a\).

Omdat het punt \((a,b)\) ook op de ellips ligt geldt ook: \(a^2+5b^2=5\).

Dus geldt: \(a=-1\) waaruit volgt dat \(b=1\) en dus \(\displaystyle\frac{h}{8}=\frac{1}{4}\quad\Longrightarrow\quad h=\frac{8}{4}=2\).

Hieruit volgt dat de hoogte van de lamp gelijk is aan \(2\).

Hoewel hiermee de opgave is opgelost, is het interessant om nog even wat verder te kijken. Merk op dat het raakpunt van de bovenste raaklijn, door de punten \((−5,0)\) en \((3,2)\), gelijk is aan: \((−1,1)\). Nu kunnen we ook het raakpunt van de onderste raaklijn aan de ellips bepalen. Deze raaklijn gaat ook door het punt \((3,2)\) en heeft dus de vorm:

\[y-2=r(x-3),\]

waarbij \(r\) de richtingscoëffiiciënt is van deze raaklijn. Deze is gelijk aan de afgeleide \(\displaystyle\frac{dy}{dx}\) in het raakpunt. Dus, als we dit punt \((c,d)\) noemen, dan volgt:

\[r=\displaystyle\frac{dy}{dx}\bigg|_{(c,d)}=-\frac{c}{4d}.\]

Het punt \((c,d)\) ligt op de raaklijn, dus geldt:

\[d-2=-\displaystyle\frac{c}{4d}(c-3)\quad\Longrightarrow\quad c^2+4d^2=3c+8d.\]

Omdat het punt \((c,d)\) ook op de ellips ligt, geldt ook: \(c^2+4d^2=5\). Dus volgt: \(3c+8d=5\).

Ten slotte, substitutie leidt dan tot: \(c=\displaystyle\frac{11}{5}\) en \(d=-\displaystyle\frac{1}{5}\). De richtingscoëfficiënt in dit punt is gelijk aan \(\displaystyle\frac{11}{4}\).

De afgeleide van de Lambert \(W\)-functie

De Lambert \(W\)-functie is de inverse van de functie \(y=xe^x\) met domein \([-1,\infty)\) en bereik \([-e^{-1},\infty)\). Hieruit volgt dat \(W(x)e^{W(x)}=x\).

Impliciet differentiëren leidt tot: \(W'(x)e^{W(x)}+W(x)\cdot W'(x)e^{W(x)}=1\;\Longleftrightarrow\;W'(x)\left(1+W(x)\right)e^{W(x)}=1\) voor \(x>-e^{-1}\).

Dus: \(W'(x)=\displaystyle\frac{1}{\left(1+W(x)\right)e^{W(x)}}\) voor \(x>-e^{-1}\). Omdat \(W(0)=0\), volgt hieruit dat \(W'(0)=1\).

Met behulp van \(W(x)e^{W(x)}=x\) volgt \(W'(x)=\displaystyle\frac{W(x)}{\left(1+W(x)\right)W(x)e^{W(x)}}=\frac{W(x)}{x\left(1+W(x)\right)}\) voor \(x>-e^{-1}\) en \(x\neq0\).

---

Laatst gewijzigd op 10 maart 2024