Analyse – Differentiëren

Definitie: De afgeleide van een functie \(f\) in een punt \(a\) is \(f'(a)=\lim\limits_{h\to0}\displaystyle\frac{f(a+h)-f(a)}{h}\) als deze limiet bestaat.

Alternatieve notatie: \(f'(a)=\lim\limits_{x\to a}\displaystyle\frac{f(x)-f(a)}{x-a}\).

Definitie: De afgeleide van \(f\) is de functie \(f'\) gegeven door \(f'(x)=\displaystyle\lim\limits_{h\to0}\frac{f(x+h)-f(x)}{h}\) voor alle \(x\) waarvoor deze limiet bestaat.

Definitie: Een functie \(f\) is differentieerbaar in \(a\) als \(f'(a)\) bestaat.

Definitie: Een functie \(f\) is differentieerbaar op een open interval \(I\) als \(f\) differentieerbaar is in elk punt in \(I\).

Stelling: Als \(f\) differentieerbaar is in \(a\), dan is \(f\) continu in \(a\).

Als \(f\) differentieerbaar is in \(a\), dan is \(y=f(a)+f'(a)(x-a)\) de raaklijn aan de grafiek van \(f\) in het punt \((a,f(a))\).

Definitie: Als \(f\) differentieerbaar is in \(a\), dan heet de functie \(L(x)=f(a)+f'(a)(x-a)\) de linearisering van \(f\) in \(a\).

Het open box probleem

We willen een open box (zonder deksel) maken uit één stuk
karton door in de vier hoeken een vierkant af te snijden:

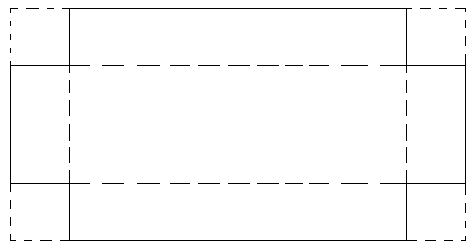Neem aan dat de vierkanten zijde \(x\) hebben en
dat de afmetingen van het rechthoekige deel
van het karton gelijk zijn aan \(24\times15\;\text{cm}\).

Wat is het maximale volume van de box?

Oplossing: Merk op dat het volume van de box wordt gegeven door \(V(x)=x(24-2x)(15-2x)\) met afgeleide

\begin{align*} V'(x)&=(24-2x)(15-2x)-2x(15-2x)-2x(24-2x)\\ &=360-78x+4x^2-78x+8x^2=360-156x+12x^2=12(3-x)(10-x). \end{align*}

Omdat de zijden \(x\), \(24-2x\) en \(15-2x\) positief moeten zijn, concluderen we dat \(x=3\) en dat leidt tot het maximale volume \(V(3)=486\).

---

Laatst gewijzigd op 1 maart 2021