Calculus – Differentiation

Definition: The derivative of a function \(f\) at a number \(a\) is \(f'(a)=\lim\limits_{h\to0}\displaystyle\frac{f(a+h)-f(a)}{h}\) if this limit exist.

Alternative notation: \(f'(a)=\lim\limits_{x\to a}\displaystyle\frac{f(x)-f(a)}{x-a}\).

Definition: The derivative of \(f\) is the function \(f'\) given by \(f'(x)=\displaystyle\lim\limits_{h\to0}\frac{f(x+h)-f(x)}{h}\) for all \(x\) for which this limit exists.

Definition: A function \(f\) is differentiable at \(a\) if \(f'(a)\) exists.

Definition: A function \(f\) is differentiable on an open interval \(I\) if \(f\) is differentiable at every number in \(I\).

Theorem: If \(f\) is differentiable at \(a\), then \(f\) is continuous at \(a\).

If \(f\) is differentiable at \(a\), then \(y=f(a)+f'(a)(x-a)\) denotes the tangent line to the graph of \(f\) at the point \((a,f(a))\).

Definition: If \(f\) is differentiable at \(a\), then the function \(L(x)=f(a)+f'(a)(x-a)\) is called the linearization of \(f\) at \(a\).

The open box problem

We want to make an open box (without lid) from one piece of cardboard by cutting off four square corners:

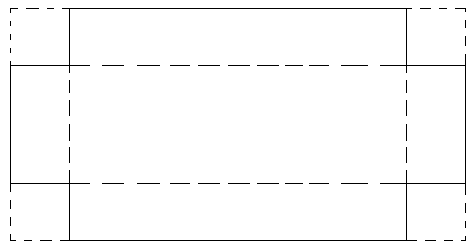Suppose that the squares have sides \(x\) and
that the dimensions of the rectangular piece
of cardboard are \(24\times15\;\text{cm}\).

What is the maximum volume of the box?

Solution: Note that the volume of the box is given by \(V(x)=x(24-2x)(15-2x)\) with derivative

\begin{align*} V'(x)&=(24-2x)(15-2x)-2x(15-2x)-2x(24-2x)\\ &=360-78x+4x^2-78x+8x^2=360-156x+12x^2=12(3-x)(10-x). \end{align*}

Since the sides \(x\), \(24-2x\) and \(15-2x\) should be positive, we conclude that \(x=3\) which leads to the maximum volume \(V(3)=486\).

---

Last modified on March 1, 2021