Calculus – Differentiation – Hyperbolic functions

The hyperbolic functions are defined as follows.

Definition: \(\sinh(x)=\displaystyle\frac{e^x-e^{-x}}{2}\), \(\cosh(x)=\displaystyle\frac{e^x+e^{-x}}{2}\) and \(\tanh(x)=\displaystyle\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\).

Rules of calculation:

1. \(\sinh(-x)=-\sinh(x)\), \(\cosh(-x)=\cosh(x)\) and \(\tanh(-x)=-\tanh(x)\);


2. \(\cosh^2(x)-\sinh^2(x)=1\);


3. \(\sinh(x+y)=\sinh(x)\cosh(y)+\cosh(x)\sinh(y)\);


4. \(\cosh(x+y)=\cosh(x)\cosh(y)+\sinh(x)\sinh(y)\).

Proof: This follows immediately from the definition:

\[\sinh(-x)=\frac{e^{-x}-e^x}{2}=-\frac{e^x-e^{-x}}{2}=-\sinh(x)\quad\textrm{and}\quad \cosh(-x)=\frac{e^{-x}+e^x}{2}=\frac{e^x+e^{-x}}{2}=\cosh(x).\]

Then we have: \(\tanh(-x)=\displaystyle\frac{\sinh(-x)}{\cosh(-x)}=-\frac{\sinh(x)}{\cosh(x)}=-\tanh(x)\). Further we have

\[\cosh^2(x)-\sinh^2(x)=\left(\frac{e^x+e^{-x}}{2}\right)^2-\left(\frac{e^x-e^{-x}}{2}\right)^2 =\frac{e^{2x}+2+e^{-2x}}{4}-\frac{e^{2x}-2+e^{-2x}}{4}=\frac{1}{2}+\frac{1}{2}=1.\]

Finally we have

\begin{align*} \sinh(x)\cosh(y)+\cosh(x)\sinh(y)&=\frac{e^x-e^{-x}}{2}\cdot\frac{e^y+e^{-y}}{2}+\frac{e^x+e^{-x}}{2}\cdot\frac{e^y-e^{-y}}{2}\\[2.5mm] &=\frac{e^{x+y}+e^{x-y}-e^{-x+y}-e^{-x-y}}{4}+\frac{e^{x+y}-e^{x-y}+e^{-x+y}-e^{-x-y}}{4}\\[2.5mm] &=\frac{2e^{x+y}-2e^{-x-y}}{4}=\frac{e^{x+y}-e^{-x-y}}{2}=\sinh(x+y) \end{align*}

and

\begin{align*} \cosh(x)\cosh(y)+\sinh(x)\sinh(y)&=\frac{e^x+e^{-x}}{2}\cdot\frac{e^y+e^{-y}}{2}+\frac{e^x-e^{-x}}{2}\cdot\frac{e^y-e^{-y}}{2}\\[2.5mm] &=\frac{e^{x+y}+e^{x-y}+e^{-x+y}+e^{-x-y}}{4}+\frac{e^{x+y}-e^{x-y}-e^{-x+y}+e^{-x-y}}{4}\\[2.5mm] &=\frac{2e^{x+y}+2e^{-x-y}}{4}=\frac{e^{x+y}+e^{-x-y}}{2}=\cosh(x+y). \end{align*}

Graphs of hyperbolic functions

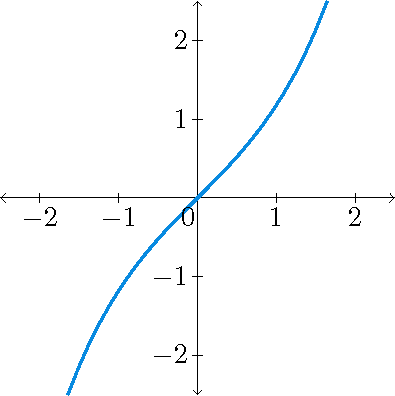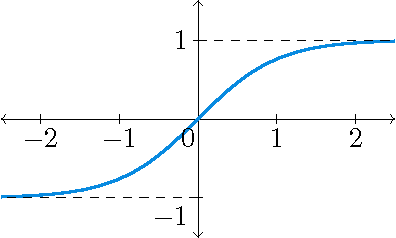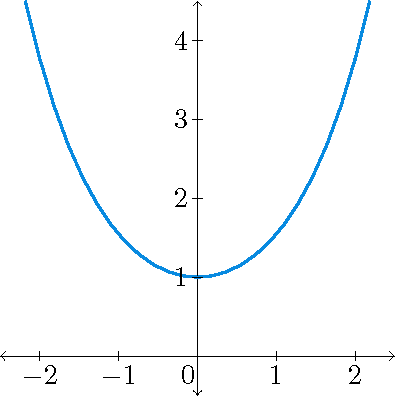\(y=\sinh(x)\)	\(y=\tanh(x)\)	\(y=\cosh(x)\)

Derivatives

Theorem: \(\displaystyle\frac{d}{dx}\sinh(x)=\cosh(x)\), \(\displaystyle\frac{d}{dx}\cosh(x)=\sinh(x)\) and \(\displaystyle\frac{d}{dx}\tanh(x)=\frac{1}{\cosh^2(x)}=1-\tanh^2(x)\).

Proof: This follows immediately from the definition:

\[\frac{d}{dx}\sinh(x)=\frac{1}{2}\frac{d}{dx}\left(e^x-e^{-x}\right)=\frac{1}{2}\left(e^x+e^{-x}\right)=\cosh(x)\quad\textrm{and}\quad \frac{d}{dx}\cosh(x)=\frac{1}{2}\frac{d}{dx}\left(e^x+e^{-x}\right)=\frac{1}{2}\left(e^x-e^{-x}\right)=\sinh(x).\]

Note that \(\displaystyle\frac{d}{dx}\tanh(x)=\frac{\cosh^2(x)-\sinh^2(x)}{\cosh^2(x)}\) which can both be written as \(\displaystyle\frac{1}{\cosh^2(x)}\) and as \(1-\tanh^2(x)\).

Inverse hyperbolic functions (area functions)

Definition:
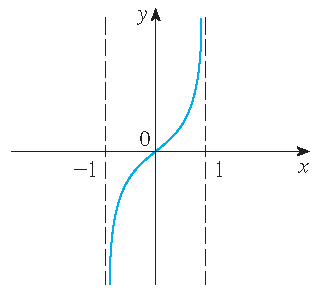
\begin{align*} y=\textrm{arsinh}(x)\quad&\Longleftrightarrow\quad\sinh(y)=x\\[2.5mm] y=\textrm{arcosh}(x)\quad&\Longleftrightarrow\quad\cosh(y)=x\quad\textrm{and}\quad y\geq0\\[2.5mm] y=\textrm{artanh}(x)\quad&\Longleftrightarrow\quad\tanh(y)=x. \end{align*}

The "ar" is short for "area" ; therefore these functions are sometimes called area functions.

Graphs of inverse hyperbolic functions

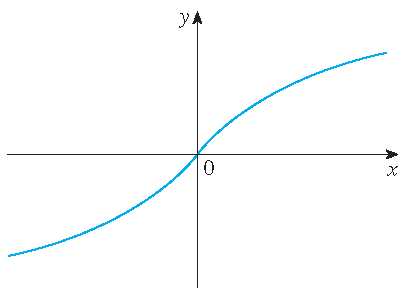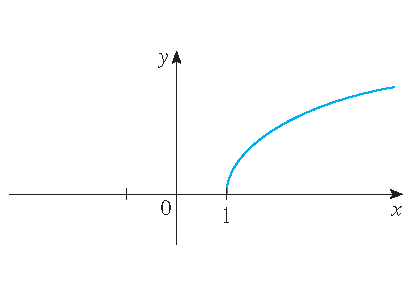\(y=\textrm{arsinh}(x)\)	\(y=\textrm{artanh}(x)\)	\(y=\textrm{arcosh}(x)\)

Theorem:
\begin{align*} \textrm{arsinh}(x)=\ln\left(x+\sqrt{1+x^2}\right),\quad x\in\mathbb{R}\\[2.5mm] \textrm{arcosh}(x)=\ln\left(x+\sqrt{x^2-1}\right),\quad x\geq1\\[2.5mm] \textrm{artanh}(x)=\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right),\quad-1 < x < 1. \end{align*}

Proof: Using the definition we have \(y=\textrm{arsinh}(x)\;\Longleftrightarrow\;\sinh(y)=x\;\Longleftrightarrow\;e^y-e^{-y}=2x\;\Longleftrightarrow\;e^{2y}-2xe^y=1\). Let \(e^y=q\), then we have

\[q^2-2xq=1\quad\Longleftrightarrow\quad(q-x)^2=1+x^2\quad\Longleftrightarrow\quad q=x\pm\sqrt{1+x^2}.\]

Since \(q=e^y\) should be positive, we conclude that \(e^y=x+\sqrt{1+x^2}\) and therefore \(y=\ln\left(x+\sqrt{1+x^2}\right)\) with \(x\in\mathbb{R}\).

Using the definition we obtain \(y=\textrm{arcosh}(x)\;\Longleftrightarrow\;\cosh(y)=x\) with \(y\geq0\). Note that \(x\geq1\). Hence we have:

\[e^y+e^{-y}=2x\quad\Longleftrightarrow\quad e^{2y}-2xe^y+1=0\quad\Longleftrightarrow\quad(e^y-x)^2=x^2-1 \quad\Longleftrightarrow\quad e^y=x\pm\sqrt{x^2-1}.\]

Since \(y\geq0\) we conclude that \(e^y\) should be at least \(1\). So: \(e^y=x+\sqrt{x^2-1}\) and therefore \(y=\ln\left(x+\sqrt{x^2-1}\right)\) with \(x\geq1\).

Using the definition we obtain \(y=\textrm{artanh}(x)\;\Longleftrightarrow\;\tanh(y)=x\;\Longleftrightarrow\;\displaystyle\frac{e^y-e^{-y}}{e^y+e^{-y}}=x\;\Longleftrightarrow\;e^y-e^{-y}=x(e^y+e^{-y})\). Hence we have

\[(1-x)e^y=(1+x)e^{-y}\quad\Longleftrightarrow\quad e^{2y}=\frac{1+x}{1-x}\quad\textrm{with}\quad -1 < x < 1.\]

This implies that \(y=\displaystyle\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)\) with \(-1 < x < 1\).

---

Last modified on October 28, 2021