TeachingCalculus – Differentiation – The chain rule
Theorem: If \(g\) is differentiable at \(x\) and \(f\) is differentiable at \(g(x)\), then the composite function \(F=f\circ g\), defined by \(F(x)=f(g(x))\), is differentiable at \(x\) and \(F'(x)=f'(g(x))g'(x)\).
In Leibniz notation, if \(y=f(u)\) and \(u=g(x)\) are both differentiable, then we have: \(\displaystyle\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\).
Applications:
Stewart §3.9, Example 1
Air is being pumped into a spherical balloon so that its volume increases at a rate of \(100\;\text{cm}^3/\text{s}\).
How fast is the radius of the balloon increasing when the diameter is \(50\;\text{cm}\)?
Solution:
The volume \(V\) of a sphere with radius \(r\) is equal to \(V=\displaystyle\frac{4}{3}\pi r^3\).
Both the volume \(V\) and the radius \(r\) depend on the time \(t\) (so: both ar functions of \(t\)).
Now we have: \(\displaystyle\frac{dV}{dt}=\frac{dV}{dr}\cdot\frac{dr}{dt}=4\pi r^2\frac{dr}{dt}\).
Now substitute \(r=25\) and \(\displaystyle\frac{dV}{dt}=100\), then we have: \(100=4\pi(25)^2\displaystyle\frac{dr}{dt}\).
This implies that \(\displaystyle\frac{dr}{dt}=\frac{100}{4\pi(25)^2}=\frac{1}{25\pi}\approx0.0127\;\text{cm}/\text{s}.\).
Stewart §3.9, Example 3
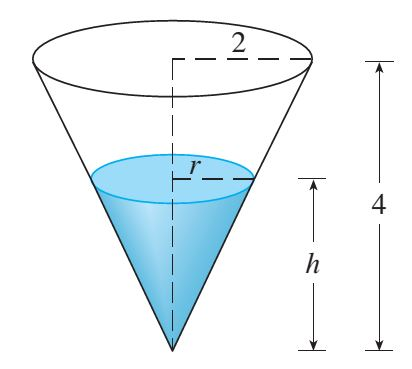
A water tank has the shape of an inverted circular cone with base radius \(2\;\text{m}\) and height \(4\;\text{m}\). If water is being pumped
into the tank at a rate of \(2\;\text{m}^3/\text{min}\), find the rate at which the water level is rising when the water is \(3\;\text{m}\) deep.
Solution:
The volume \(V\) is given by \(V=\displaystyle\frac{1}{3}\pi r^2h\).
In order to write \(V\) as a function of \(h\) alone, we eliminate \(r\) using similar triangles:
\[\frac{r}{h}=\frac{2}{4}\quad\Longrightarrow\quad r=\frac{h}{2}.\]Hence we have: \(V=\displaystyle\frac{1}{3}\pi\left(\frac{h}{2}\right)^2h=\frac{1}{12}\pi h^3\).
Since both the volume \(V\) and the height \(h\) are functions of the time \(t\), we find that \(\displaystyle\frac{dV}{dt}=\frac{1}{4}\pi h^2\frac{dh}{dt}\).
Now we substitute \(h=3\) and \(\displaystyle\frac{dV}{dt}=2\) to obtain \(2=\displaystyle\frac{1}{4}\pi(3)^2\frac{dh}{dt}\quad\Longrightarrow\quad\frac{dh}{dt}=\frac{8}{9\pi}\approx0.28\;\text{m}/\text{min}\).
Last modified on March 1, 2021
