OnderwijsAnalyse – Differentiëren – De kettingregel
Stelling: Als \(g\) differentieerbaar is in \(x\) en \(f\) is differentieerbaar in \(g(x)\), dan is de samengestelde functie \(F=f\circ g\), gedefinieerd door \(F(x)=f(g(x))\), differentieerbaar in \(x\) en \(F'(x)=f'(g(x))g'(x)\).
In de notatie van Leibniz, als \(y=f(u)\) en \(u=g(x)\) beide differentieerbaar zijn, dan geldt: \(\displaystyle\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\).
Toepassingen:
Stewart §3.9, Voorbeeld 1
Er wordt lucht in een bolvormige ballon gepompt zodanig dat het volume toeneemt met een snelheid van \(100\;\text{cm}^3/\text{s}\).
Hoe snel neemt dan de straal van de ballon toe als de diameter gelijk is aan \(50\;\text{cm}\)?
Oplossing:
Het volume \(V\) van een bol met straal \(r\) is gelijk aan \(V=\displaystyle\frac{4}{3}\pi r^3\).
Zowel het volume \(V\) als de straal \(r\) hangen af van de tijd \(t\) (dus: beide zijn functies van \(t\)).
Nu geldt: \(\displaystyle\frac{dV}{dt}=\frac{dV}{dr}\cdot\frac{dr}{dt}=4\pi r^2\frac{dr}{dt}\).
Substitueer nu \(r=25\) en \(\displaystyle\frac{dV}{dt}=100\), dan volgt: \(100=4\pi(25)^2\displaystyle\frac{dr}{dt}\).
Daaruit volgt dat \(\displaystyle\frac{dr}{dt}=\frac{100}{4\pi(25)^2}=\frac{1}{25\pi}\approx0.0127\;\text{cm}/\text{s}.\).
Stewart §3.9, Voorbeeld 3
Een watertank heeft de vorm van een omgekeerde cirkelvormige kegel met straal \(2\;\text{m}\) aan de bovenkant en hoogte \(4\;\text{m}\).
Als er water in de tank wordt gepompt met een snelheid van \(2\;\text{m}^3/\text{min}\), bepaal dan de snelheid waarmee het water stijgt op
het moment dat de hoogte daarvan \(3\;\text{m}\) is.
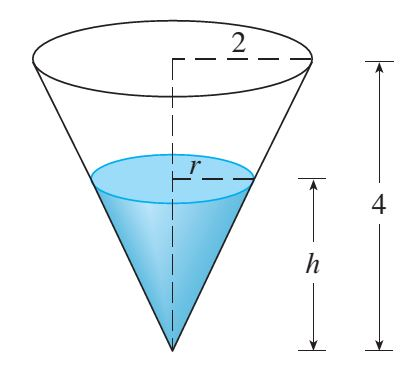Oplossing:
Het volume \(V\) wordt gegeven door \(V=\displaystyle\frac{1}{3}\pi r^2h\).
Om \(V\) te kunnen schrijven als functie van alleen \(h\), elimineren we \(r\) door gebruik te maken van congruente driehoeken:
\[\frac{r}{h}=\frac{2}{4}\quad\Longrightarrow\quad r=\frac{h}{2}.\]Dus geldt: \(V=\displaystyle\frac{1}{3}\pi\left(\frac{h}{2}\right)^2h=\frac{1}{12}\pi h^3\).
Omdat zowel het volume \(V\) als de hoogte \(h\) functies zijn van de tijd \(t\), volgt dat \(\displaystyle\frac{dV}{dt}=\frac{1}{4}\pi h^2\frac{dh}{dt}\).
Nu substitueren we \(h=3\) en \(\displaystyle\frac{dV}{dt}=2\) en vinden dat \(2=\displaystyle\frac{1}{4}\pi(3)^2\frac{dh}{dt}\quad\Longrightarrow\quad\frac{dh}{dt}=\frac{8}{9\pi}\approx0.28\;\text{m}/\text{min}\).
Laatst gewijzigd op 1 maart 2021
