TeachingCalculus – Inverse functions – Lambert \(W\) function
The Lambert \(W\) function is "the inverse" of the function \(y=xe^x\). Note that this function exists for all \(x\in\mathbb{R}\), however it is not one-to-one on \(\mathbb{R}\). The function attains for \(x=-1\) a minimum value: \(-e^{-1}\). The function is one-to-one with domain \([-1,\infty)\) and range \([-e^{-1},\infty)\), and also with domain \((-\infty,-1]\) and range \([-e^{-1},0)\).
Definition: The Lambert \(W\) function is the inverse of the function \(y=xe^x\) with domain \([-1,\infty)\).
Hence: \(y=W(x)\) with \(x=ye^y\) or equivalently \(W(x)e^{W(x)}=x\). This function is also indicated as \(W_0(x)\).
The other "branch", the inverse of \(y=xe^x\) with domain \((-\infty,-1]\), is then indicated as \(W_{-1}(x)\).
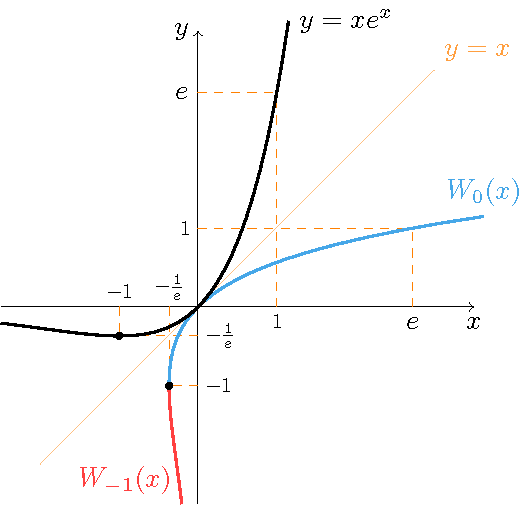
Some properties: \(W_{-1}(-e^{-1})=W(-e^{-1})=-1\), \(W(0)=0\) and \(W(e)=1\).
Furthermore, we have: \(W(xe^x)=x\) for \(x\geq-1\) and \(W_{-1}(xe^x)=x\) for \(x\leq-1\).
This implies that \(W(x\ln(x))=\ln(x)\) for \(x\geq e^{-1}\) and \(W_{-1}(x\ln(x))=\ln(x)\) for \(x\leq e^{-1}\).
Last modified on March 10, 2024
