Calculus – Inverse functions – More on inverse trigonometric functions

Since we have (see: Stewart Appendix D)

\[\left\{\begin{array}{l}\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)\\[2.5mm] \cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\end{array}\right.\]

we find that

\[\tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\frac{\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)}{\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)} =\frac{\frac{\sin(\alpha)}{\cos(\alpha)}+\frac{\sin(\beta)}{\cos(\beta)}}{1-\frac{\sin(\alpha)\sin(\beta)}{\cos(\alpha)\cos(\beta)}} =\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)}.\]

If we set \(x=\tan(\alpha)\) or \(\alpha=\arctan(x)\) and \(y=\tan(\beta)\) or \(\beta=\arctan(y)\) we obtain that

\[\arctan(x)+\arctan(y)=\arctan\left(\frac{x+y}{1-xy}\right)\quad(\text{mod}\;\pi).\]

For instance, this implies that

\[\arctan(\tfrac{1}{2})+\arctan(\tfrac{1}{3})=\arctan\left(\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}\cdot\frac{1}{3}}\right)=\arctan(1)=\frac{1}{4}\pi\]

and

\[\arctan(2)+\arctan(3)=\arctan\left(\frac{2+3}{1-2\cdot3}\right)+\pi=\arctan(-1)+\pi=-\frac{1}{4}\pi+\pi=\frac{3}{4}\pi.\]

Since \(\arctan(1)=\frac{1}{4}\pi\), this implies that

\[\arctan(1)+\arctan(2)+\arctan(3)=\pi.\]

This result can also be obtained by an elegant geometric proof:

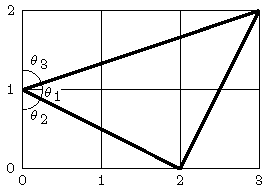
Note that the triangle is isosceles with a right angle, which implies that \(\theta_1=\arctan(1)=\frac{1}{4}\pi\). Furthermore, \(\theta_2=\arctan(2)\) and \(\theta_3=\arctan(3)\). We conclude that \(\theta_1+\theta_2+\theta_3=\pi\).

---

Similarly, we have

\[\arctan(\tfrac{1}{2})+\arctan(3)+\arctan(7)=\pi.\]

To prove this, note that

\[\arctan(3)+\arctan(7)=\arctan\left(\frac{3+7}{1-3\cdot7}\right)+\pi=\arctan(-\tfrac{1}{2})+\pi.\]

and

\[\arctan(\tfrac{1}{2})+\arctan(-\tfrac{1}{2})=\arctan\left(\frac{\frac{1}{2}-\frac{1}{2}}{1+\frac{1}{4}}\right)=\arctan(0)=0.\]

Applying the formula once more we find that

\[\arctan(x)+\arctan(y)+\arctan(z)=\arctan\left(\frac{\frac{x+y}{1-xy}+z}{1-\frac{x+y}{1-xy}\cdot z}\right) =\arctan\left(\frac{x+y+z-xyz}{1-xy-xz-yz)}\right)\quad(\text{mod}\;\pi).\]

Other remarkable identities are:

\[\left\{\begin{array}{l}\arctan(7)-2\arctan(2)+\arctan(1)=0\\[2.5mm] \arctan(13)-\arctan(8)-\arctan(5)+\arctan(4)=0\\[2.5mm] \arctan(8)+\arctan(5)+\arctan(2)-\arctan(1)=\pi\\[2.5mm] \arctan(8)+\arctan(7)+\arctan(5)-\arctan(2)=\pi\\[2.5mm] \arctan(13)+\arctan(7)+\arctan(4)-\arctan(2)=\pi.\end{array}\right.\]

Since \(\arctan(1)=\frac{1}{4}\pi\) we conclude that

\[2\arctan(2)-\arctan(7)=\tfrac{1}{4}\pi\quad\text{and}\quad\arctan(2)+\arctan(5)+\arctan(8)=\tfrac{5}{4}\pi.\]

---

Last modified on March 1, 2021